Height of Binary Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download

Introduction

The height or depth of a binary tree can be defined as the maximum or the largest number of edges from a leaf node to the root node or root node to the leaf node. The root node will be at level zero that means if the root node doesn't have any of the child nodes connected to it then the height or depth of the particular binary tree is said to be zero.

Let us take an example for a better understanding of the height of the binary tree.

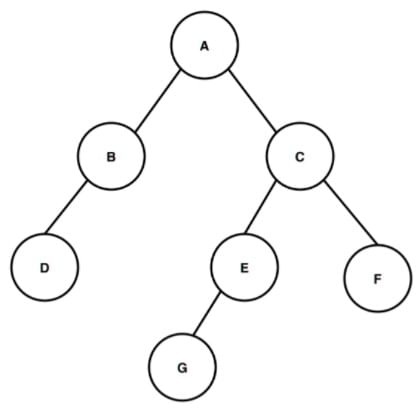
In the above image, we have a binary tree starting from the root node named A. The root node A is having two child nodes B and C as the left child and right child respectively. And similarly left child node B has only one left child node named D and right child node C has two child nodes E and F from which node E has node G as the only left child.

Now let's calculate the height of this binary tree. Count the number of edges starting from the root node to the deepest leaf node for calculating the height of the binary tree. The deepest node that is present in this binary tree is the node G. So, for the calculation of the height or depth of this binary tree we need to calculate the number of edges between the root node and the deepest node G. The first edge is from node A to node C, the second edge is from the node C to node E and the third edge is from the node E to node G. So, for traversing from the root node A to the deepest node G there are three edges, so the height or depth of the binary tree is 3. The path that we followed to move from the root to the deepest leaf node is A > C > E > G and this path covers three edges during the traversal, that is why according to the definition of the height of the binary tree the height of this binary tree is 3.

Ways to Find Height of Binary Tree

Now, let us write code to find the height of a binary tree. There are two ways to find the height of the binary tree. One is the recursive method and the other one is the non-recursive method that will make use of the Queue data structure to calculate the height of the binary tree.

1. Recursive Way
First, let's see the recursive way to find the height of the binary tree.
Code:

// Java program to create and to find the height of a binary tree by recursive way     

// util package is imported to use classes like Queue and LinkedList  

import java.util.*;    

// A class named Node is created representing a single node of a binary tree  

class Node{     

  // The class Node has three class variables named key and left and right of int type and Node type respectively.    

  // the key variable holds the actual value that is assigned to that node of the binary tree  

  int key;  

  // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree  

  Node left, right;  

// a parameterized constructor is created to create and add data to the node at the same time.  

  public Node(int item)  

  {  

    key = item;  

    left = right = null;  

  }   

 }  

// end of node class definition    

// A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise.  

class BinaryTree{  

  // A static variable named root_node is created that will represent the node of the binary tree  

  static Node root_node;  

// A parametrized constructor of the BinaryTree class is written having the key as a parameter  

  BinaryTree(int key)  

  {  

// here we are constructing a new node and assigning it to the root node  

    root_node = new Node(key);  

  }   

  BinaryTree()  

  {  

    root_node = null;  

  }  

// a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node    

 public static void printTree()  

    {  

        int h = height(root_node);  

        int i;  

        for (i=1; i<=h; i++){  

            printCurrentLevel(root_node, i);  

            System.out.println();  

          }  

    }  

 // a public static function named height is created to fund the height of the binary tree starting from the root node to the deepest leaf node that is present in the binary tree  

  // the root node of the binary tree is passed as a parameter to the public static function named height  

// the height function is called recursively until the node returned is NULL to find the height of the binary tree  

    public static int height(Node root){  

      // the root is null then the height of the tree will be Zero  

        if (root == null)  

           return 0;  

        else  

        {  

            /* compute  height of each subtree */  

            int lheight = height(root.left);  

            int rheight = height(root.right);    

            /* use the larger one */  

            // height of both the sub trees is calcualted and which one is higher is used.   

            if (lheight > rheight)  

                return(lheight+1);  

            else   

                return(rheight+1);  

        }  

    }  

// a Public static function named printCurrentLevel is created to print al the nodes that are present in that level   

// this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level

   public static void printCurrentLevel (Node root ,int level)  

    {  

        if (root == null)  

            return;  

        if (level == 1)  

            System.out.print(root.key + " ");  

        else if (level > 1)  

        {  

            printCurrentLevel(root.left, level-1);  

            printCurrentLevel(root.right, level-1);  

        }  

    }  

//the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree  

  public static void main(String[] args){  

      // first of all we have created an Object of the BinaryTree class that will represent the binary tree  

    BinaryTree tree = new BinaryTree();     

    // now a new node with the value as 150 is added as the root node to the Binary Tree  

    tree.root_node = new Node(150);  

    // now a new node with the value 250 is added as a left child to the root node   

    tree.root_node.left = new Node(250);  

    // now a new node with the value 270 is added as a right child to the root node   

    tree.root_node.right = new Node(270);  

    // now a new node with the value 320 is added as a left child to the left node of the previous level node   

    tree.root_node.left.left = new Node(320);  

    // now a new node with the value 350 is added as a right child to the right node of the previous level node  

    tree.root_node.left.right = new Node(350);  

    /*  

               150 

            /          \ 

       250         270 

        /     \       /      \ 

      320 350  null  null 

*/  

       System.out.println("Printing the nodes of tree level wise :");  

    System.out.println("Level order traversal : ");  

    tree.printTree();  

    // height of the binary tree is calculated bypassing the root as parameter to the height() function.  

    int h = tree.height(tree.root_node)  

    System.out.println("The height of the Binary tree is : " + h );  

  }  

}  

// end of the BinaryTree class  

Output: The output of the above code is:

Printing the nodes of tree level wise:

Level order traversal: 

(level 0) 150 

(level 1) 250 270 

(level 2) 320 350 

The height of the Binary tree is: 2

In a recursive way, we have called the height() function repeatedly to find the height of the binary tree. The root node of the binary tree is passed as a parameter to the height() function. The height() function calculates the height of both the subtrees of the root node and which one among both of the heights is higher is considered as the height of the binary tree.

2. Non-Recursive Way
Now let see the non-recursive way to find the height of the binary tree.
Code:

// A C++ program to create and to find the height of a binary tree by non recursive way  

// iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively    

#include <iostream>  

#include <bits/stdc++.h>  

using namespace std;  

// A struct named Node is created representing a single node of a binary tree  

struct Node  

{  

    // The struct Node has three variables named key and left and right of int type and Node type respectively.    

    // the key variable holds the actual value that is assigned to that node of the binary tree  

    int key;   

  // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree  

    struct Node* left, *right;  

};    

// A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing    

Node* newNode(int key)  

{  

    Node* temp = new Node;  

    temp->key = key;  

    temp->left = temp->right = NULL;  

    return (temp);  

}    

// A function named height is created to find the height of the binary tree with non recursive way
// The parameter to the height function is the root node of the binary tree that will be present at level zero  

// In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until  

// the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure.      

int height(struct Node* root){    

    //Initialising a variable to count the  

    //height of tree  

    int depth = 0;    

    queue<Node*>q;        

    //Pushing first level element along with NULL  

    q.push(root);  

    q.push(NULL);  

    while(!q.empty()){  

        Node* temp = q.front();  

        q.pop();  

      //When NULL encountered, increment the value  

        if(temp == NULL){  

            depth++;  

        }            

        //If NULL not encountered, keep moving  

        if(temp != NULL){  

            if(temp->left){  

                q.push(temp->left);  

            }  

            if(temp->right){  

                q.push(temp->right);  

            }  

        }       

        //If queue still have elements left,  

        //push NULL again to the queue.  

        else if(!q.empty()){  

            q.push(NULL);  

        }  

    }  

    return depth;  

}

// Start of the main function  

int main()  

{  

    // first of all we have created an Object of the struct Node that will represent the binary tree  

    // the value of the root node is 10  

    Node *root = newNode(10);  

   // now a new node with the value 20 is added as a left child to the root node   

    root->left = newNode(20);  

    // now a new node with the value 30 is added as a right child to the root node   

    root->right = newNode(30);  

    // now a new node with the value 40 is added as a left child to the left node of the previous level node   

    root->left->left = newNode(40);  

    // now a new node with the value 50 is added as a right child to the left node of the previous level node  

    root->left->right = newNode(50);   

      /*  

               10 

             /          \ 

         20         30 

        /     \       /      \ 

      40  50  null  null 

  */  

   cout<<"The Height(Depth) of tree is: "<<height(root);  

    cout<<endl;  

}  

// end of the main function

Output:

The Height(Depth) of the tree is: 2

In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.

In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.

Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.