Heights and Distances: Solved Examples | Quantitative Aptitude (Quant) - CAT PDF Download
1. Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
A. 173 m
B. 200 m
C. 273 m
D. 300 m
Answer: C
Explanation:
Let AB be the lighthouse and C and D be the positions of the ships.

2. A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?
A. 43 units
B. 8 units
C. 12 units
D. Data inadequate
E. None of these
Answer: D
Explanation:
One of AB, AD and CD must have given.

So, the data is inadequate.
3. The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
A. 2.3 m
B. 4.6 m
C. 7.8 m
D. 9.2 m
Answer: D
Explanation:
Let AB be the wall and BC be the ladder.

4. An observer 1.6 m tall is 20√3 away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The heights of the tower is:
A.21.6 m
B. 23.2 m
C. 24.72 m
D. None of these
Answer: A
Explanation:
Let AB be the observer and CD be the tower.

5. From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:
A. 149 m
B. 156 m
C. 173 m
D. 200 m
Answer: C
Explanation:
Let AB be the tower.

6. The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 12.4 m away from the wall. The length of the ladder is:
A. 14.8 m
B. 6.2 m
C. 12.4 m
D. 24.8 m
Answer: D
Explanation:

Consider the diagram shown above where PR represents the ladder and RQ represents the wall.
cos 60° = PQ/PR
1/2 = 12.4/PR
PR = 2 × 12.4 = 24.8 m
7. A man on the top of a vertical observation tower observers a car moving at a uniform speed coming directly towards it. If it takes 8 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower?
A. 8 min 17 second
B. 10 min 57 second
C. 14 min 34 second
D. 12 min 23 second
Answer: B
Explanation:
Consider the diagram shown above. Let AB be the tower. Let D and C be the positions of the car.
Then, ∠ADC = 30° , ∠ACB = 45°
Let AB = h, BC = x, CD = y
tan45º = AB/BC = h/x
⇒ 1 = h/x
⇒ h = x .... (1)
tan 30º = AB/BD = AB/(BC + CD) = H/x+y
⇒ 1√3 = h/x + y
⇒ x + y = √3h
⇒ y = √3h - x
⇒ y = √3h - h (∵ Substituted the value of x from equation 1 )
⇒ y = h(√3 - 1)
Given that distance y is covered in 8 minutes.
i.e, distance h(√3 - 1) is covered in 8 minutes.
Time to travel distance x
= Time to travel distance h (∵ Since x = h as per equation 1).
Let distance h is covered in t minutes.
since distance is proportional to the time when the speed is constant, we have

≈ 10 minutes 57 seconds
8. A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man's eye when at a distance of 100 metres from the tower. After 10 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
A. 26.28 km/hr
B. 32.42 km/hr
C. 24.22 km/hr
D. 31.25 km/hr
Answer: A
Explanation: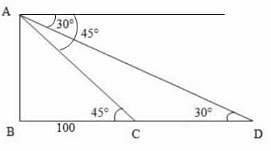
Consider the diagram shown above.
Let AB be the tower. Let C and D be the positions of the boat
Then, angleACB = 45° , angleADC = 30°, BC = 100 m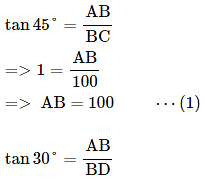
(∵ Substituted the value of AB from equation 1)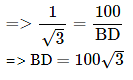
CD = (BD - BC) = (100 √3 − 100) = 100 (√3 − 1)
It is given that the distance CD is covered in 10 seconds. i.e., the distance 100(√3 − 1) is covered in 10 seconds.
Required speed
=Distance/Time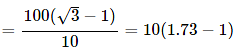
= 7.3 meter/seconds
= 7.3 × 18/5 km/hr = 26.28 km/hr.
9. The top of a 15 metre high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
A. 5 metres
B. 8 metres
C. 10 metres
D. 12 metres
Answer: C
Explanation: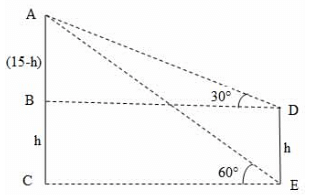
Consider the diagram shown above. AC represents the tower and DE represents the pole.
Given that AC = 15 m, angleADB = 30°, angleAEC = 60°
Let DE = h
Then, BC = DE = h,
AB = (15-h) (∵ AC=15 and BC = h),
BD = CE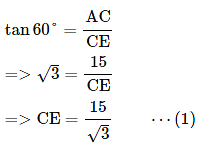
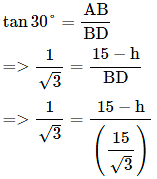
(∵ BD = CE and substituted the value of CE from equation 1)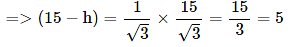
=> h = 15 − 5 = 10 m
i.e., height of the electric pole = 10 m
10. The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 40 m towards the tower, the angle of elevation of the top of the tower increases by 15°. The height of the tower is:
A. 64.2 m
B. 62.2 m
C. 52.2 m
D. 54.6 m
Answer: D
Explanation: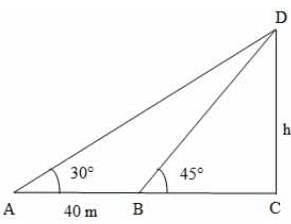
Let DC be the tower and A and B be the positions of the observer such that AB = 40 m
We have ∠DAC = 30°, ∠DBC = 45°
Let DC = h
tan 30° = DC/AC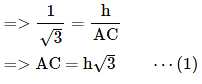
tan 45° = DC/BC
=> 1 = h/BC
=> BC = h ⋯(2)
We know that, AB = (AC - BC)
=> 40 = (AC - BC)
=> 40 = ( h√3 − h) [∵ from (1) & (2)]
=> 40 = h (√3 − 1)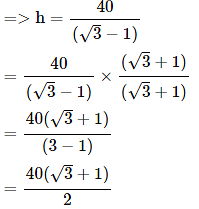
= 20 (√3 + 1) = 20 (1.73 + 1) = 20 × 2.73 = 54.6 m
11. On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 600 m, the distance between the objects is approximately equal to :
A. 272 m
B. 284 m
C. 288 m
D. 254 m
Answer: D
Explanation: 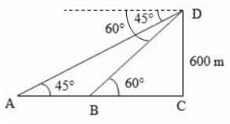
Let DC be the tower and A and B be the objects as shown above.
Given that DC = 600 m , ∠DAC = 45°, ∠DBC = 60°
tan 60° = DC/BC
√3 = 600/BC
BC = 600√3 ⋯ ( 1 )
tan 45° = DC/AC
1 = 600/AC
AC= 600 ⋯ ( 2 )
Distance between the objects
= AB = (AC - BC)
= 600 − 600/√3 [∵ from (1) and (2)]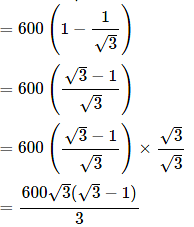
= 200 √3(√3 − 1)
= 200(3 − √3)
= 200 (3 − 1.73)
= 254 m
12. A ladder 10 m long just reaches the top of a wall and makes an angle of 60° with the wall. Find the distance of the foot of the ladder from the wall (√3 = 1.73)
A. 4.32 m
B. 17.3 m
C. 5 m
D. 8.65 m
Answer: D
Explanation:
Let BA be the ladder and AC be the wall as shown above. Then the distance of the foot of the ladder from the wall = BC
Given that BA = 10 m , ∠BAC = 60°
sin 60° = BC/BA
√3/2 = BC/10
BC = 10 × √3/2 = 5 × 1.73 = 8.65 m
13. From a tower of 80 m high, the angle of depression of a bus is 30°. How far is the bus from the tower?
A. 40 m
B. 138.4 m
C. 46.24 m
D. 160 m
Answer: B
Explanation:
Let AC be the tower and B be the position of the bus. Then BC = the distance of the bus from the foot of the tower.
Given that height of the tower, AC = 80 m and the angle of depression, ∠DAB = 30°
∠ABC = ∠DAB = 30° (because DA || BC)
tan 30° = AC/BC
=> tan 30° = 80/BC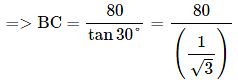
= 80 × 1.73 = 138.4 m
i.e., Distance of the bus from the foot of the tower = 138.4 m
14. The angle of elevation of the top of a lighthouse 60 m high, from two points on the ground on its opposite sides are 45° and 60°. What is the distance between these two points?
A. 45 m
B. 30 m
C. 103.8 m
D. 94.6 m
Answer: D
Explanation: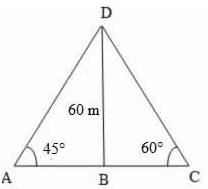
Let BD be the lighthouse and A and C be the two points on ground. Then, BD, the height of the lighthouse = 60 m
∠BAD = 45° , ∠BCD = 60°
tan 45° = BD/BA
⇒ 1 = 60/BA
⇒ BA = 60 m ⋯ ( 1 )
tan 60° = BD/BC
⇒ √3 = 60/BC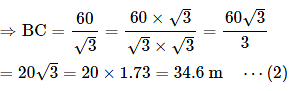
Distance between the two points A and C
= AC = BA + BC
= 60 + 34.6 [∵ Substituted value of BA and BC from (1) and (2)]
= 94.6 m
15. From the top of a hill 100 m high, the angles of depression of the top and bottom of a pole are 30° and 60° respectively. What is the height of the pole?
A. 52 m
B. 50 m
C. 66.67 m
D. 33.33 m
Answer: C
Explanation:
Consider the diagram shown above. AC represents the hill and DE represents the pole
Given that AC = 100 m
∠XAD = ∠ADB = 30° (∵ AX || BD)
∠XAE = ∠AEC = 60° (∵ AX || CE)
Let DE = h
Then, BC = DE = h,
AB = (100-h) (∵ AC=100 and BC = h),
BD = CE
(∵ BD = CE and substituted the value of CE from equation 1)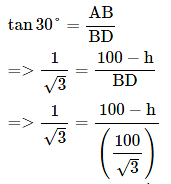
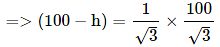
= 100/3 = 33.33
=> h = 100 − 33.33 = 66.67 m
i.e., the height of the pole = 66.67 m
16. A vertical tower stands on ground and is surmounted by a vertical flagpole of height 18 m. At a point on the ground, the angle of elevation of the bottom and the top of the flagpole are 30° and 60° respectively. What is the height of the tower?
A. 9 m
B. 10.40 m
C. 15.57 m
D. 12 m
Answer: A
Explanation: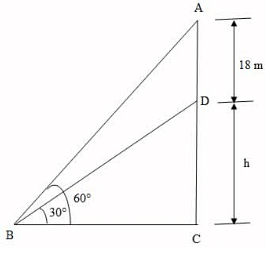
Let DC be the vertical tower and AD be the vertical flagpole. Let B be the point of observation.
Given that AD = 18 m, ∠ABC = 60°, ∠DBC = 30°
Let DC be h.
tan 30° = DC/BC
1√3 = h/BC
h = BC/√3⋯ (1)
tan 60° = AC/BC
18 + h = BC × √3 ⋯(2)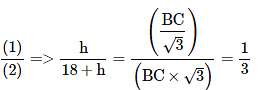
=> 3 h = 18 + h
=> 2 h = 18
=> h = 9 m
i.e., the height of the tower = 9 m
17. A balloon leaves the earth at a point A and rises vertically at uniform speed. At the end of 2 minutes, John finds the angular elevation of the balloon as 60°. If the point at which John is standing is 150 m away from point A, what is the speed of the balloon?
A. 0.63 meter/sec
B. 2.16 meter/sec
C. 3.87 meter/sec
D. 0.72 meter/sec
Answer: B
Explanation: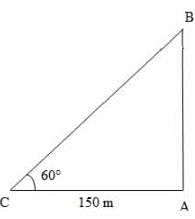
Let C be the position of John. Let A be the position at which balloon leaves the earth and B be the position of the balloon after 2 minutes.
Given that CA = 150 m, ∠BCA = 60°
tan60°= BA/CA
√3 = BA/150
BA = 150√3
i.e, the distance travelled by the balloon = 150√3 meters time taken = 2 min = 2 × 60 = 120 seconds
Speed = Distance/Time
= 150√3/120 = 1.25 √3
= 1.25 × 1.73 = 2.16 meter/second
18. The angles of depression and elevation of the top of a wall 11 m high from top and bottom of a tree are 60° and 30° respectively. What is the height of the tree?
A. 22 m
B. 44 m
C. 33 m
D. None of these
Answer: B
Explanation: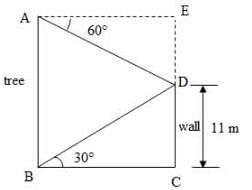
Let DC be the wall, AB be the tree.
Given that ∠DBC = 30°, ∠DAE = 60°, DC = 11 m
tan 30° = DC/BC
1√3 = 11/BC
BC = 11√3m
AE = BC = 11√3 m ⋯ (1)
tan 60 ° = ED/AE
√3 = ED/11√3 [∵ Substituted value of AE from (1)]
ED = 11√3 × √3 = 11 × 3 = 33
Height of the tree
= AB = EC = (ED + DC)
= (33 + 11) = 44 m
19. Two vertical poles are 200 m apart and the height of one is double that of the other. From the middle point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary. Find the heights of the poles.
A. 141 m and 282 m
B. 70.5 m and 141 m
C. 65 m and 130 m
D. 130 m and 260 m
Answer: B
Explanation: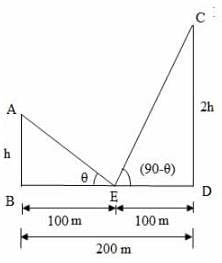
Let AB and CD be the poles with heights h and 2h respectively.
Given that distance between the poles, BD = 200 m
Let E be the middle point of BD,
∠AEB = θ ∠CED = (90-θ) (∵ given that angular elevations are complementary)
Since E is the middle point of BD, we have BE = ED = 100 m
From the right ΔABE,
tanθ = AB/BE
tanθ = h/100
h = 100 tan θ ⋯ ( 1 )
From the right ΔEDC, 
=> √2h = 100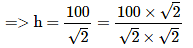
= 50√2 = 50 × 1.41 = 70.5
=> 2h = 2 × 70.5 = 141
i.e., the height of the poles are 70.5 m and 141 m.
20. To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and he is 5 m away from the wall, what is the length of the window?
A. 8.65 m
B. 2 m
C. 2.5 m
D. 3.65 m
Answer: D
Explanation: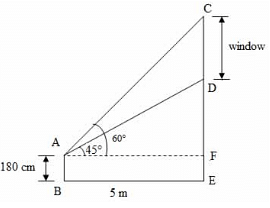
Let AB be the man and CD be the window
Given that the height of the man, AB = 180 cm, the distance between the man and the wall, BE = 5 m,
∠DAF = 45° , ∠CAF = 60°
From the diagram, AF = BE = 5 m
From the right ΔAFD,
tan 45 ° = DF/AF
1 = DF/5
DF = 5 ⋯ ( 1 )
From the right ΔAFC,
tan 60 ° = CF/AF
√3 = CF/5
CF = 5√3 ⋯ ( 2 )
Length of the window
= CD = (CF - DF)
= 5 √ 3 − 5 [∵ Substituted the value of CF and DF from (1) and (2)]
= 5 (√3 − 1) = 5 (1.73 − 1)
= 5 × 0.73 = 3.65 m
|
196 videos|131 docs|110 tests
|
FAQs on Heights and Distances: Solved Examples - Quantitative Aptitude (Quant) - CAT
| 1. What are some common applications of heights and distances in real life? |  |
| 2. How can heights and distances be measured accurately? |  |
| 3. What is the difference between angle of elevation and angle of depression? |  |
| 4. Can heights and distances be calculated without using trigonometry? |  |
| 5. What are the limitations of using heights and distances in practical scenarios? |  |

|
Explore Courses for CAT exam
|

|


















