Heron’s Formula Class 9 Worksheet Maths Chapter 10
Multiple Choice Questions
Q1: The difference between sides at right angles in a right angled triangle is 14 cm. The area of the triangle is 120 cm2. The perimeter of the triangle is
(a) 80
(b) 45
(c) 60
(d) 64
Ans: (c)
Let y be one of the at right angle ,then another side will be y-14
Now we know that
A = (1/2)BH
120 = (1/2)y(y - 14)
y2 - 14y - 240
(y - 24)(y + 10) = 0
y = 24
So other side is 10
From pythogrous theorem
So perimeter will be =10+24+26=60 cm
Q2: ABCD is a trapezium with AB = 10cm, AD = 5 cm, BC = 4 cm and DC = 7 cm? Find the area of the ABCD
Find the area of the ABCD
(a) 34 cm2
(b) 28cm2
(c) 20 cm2
(d) None of these
Ans: (a)
BC is the altitude between the two parallel sides AB and DC
So Area of trapezium will be given by
Q3: Find the area and perimeter of the right angle triangle whose hypotenuse is 5 cm and Base is 4 cm
(a) 6 cm2 ,12 cm
(b) 12 cm2 ,14 cm
(c) 4 cm2, 6 cm
(d) 12 cm2 ,6 cm
Ans: (a)
By pythogorous theorem
So Area =(1/2) XBase X height = 6 cm2
Perimeter = 5 + 4 + 3 = 12 cm
Q4: In an isosceles triangle ?ABC with AB = AC = 13 cm. D is mid point on BC. Also BC=10 cm
Which of the following is true?
(a) Area of Triangle ABD and ADC are equal
(b) Area of triangle ABD is 30 cm2
(c) Area of triangle ABC is 60 cm2
(d) All the above
Ans: (d)
ABD an ADC are congruent triangle, So Area of Triangle ABD and ADC are equal
Also From pythogorous theorem, AD will be given as
So Area of triangle ABC = (1/2)X base X height = 60 cm2
Q5: A triangle and a parallelogram have the same base and the same area. The sides of the triangle are 26 cm and 30 cm and parallelogram stands on the base 28 cm. calculate the height of the parallelogram
(a) 12 cm
(b) 14 cm
(c) 10cm
(d) 13 cm
Ans: (a)
For triangle, all the sides are given, calculating the area using Heron formula
A = 336 cm2
Now for parallelogram, Area is given by
A = Base X Altitude
336 = 28 X H
Or H = 12 cm
True / False
Q1: Heron formula for area of triangle is not valid of all triangles
Ans: False
Q2: If each side of the triangles is tripled, the area will becomes 9 times.
Ans: True
Q3: Base and corresponding altitude of the parallelogram are 8 and 5 cm respectively. Area of parallelogram is 40 cm2.
Ans: True
Q4: If each side of triangle is doubled, the perimeter will become 4 times.
Ans: False
Q5: If p is the perimeter of the triangle of sides a,b,c ,the area of triangle is.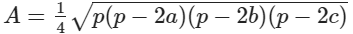
Ans: True
Q6: When two triangles are congruent, there areas are same.
Ans: True
Q7: Heron’s belongs to America.
Ans: False
Q8: If the side of the equilateral triangle is a rational number, the area would always be irrational number.
Ans: True
Concepts Questions
Q1: Find the area of a triangle having sides as a=5 cm ,b=4 cm,c=3 cm.
Ans: 
Area 
Q2: Find the area of an quilateral triangle having side a=2 cm
Ans: Area of equilateral
Q3: Find the area of a right angle triangle have base=4 cm and Height =3 cm
Ans: Area of triangle
A = (1/2)BH = 6cm2
Q4: Find the area of a Parallelogram whose two sides are 10 cm and 16 cm and diagonal is 14 cm.
Ans: In parallelogram whose two sides and diagonal are given, Area is given by
Where 
So s=20cm
So A=80(3)1/2cm2
Q5: Rhombus of diagonals to 10 and 24 cm. Find its area.
Ans: Area is given by
A=(1/2)d1d2 = 120cm2
|
44 videos|412 docs|54 tests
|
FAQs on Heron’s Formula Class 9 Worksheet Maths Chapter 10
| 1. What is Heron's Formula and how is it used to calculate the area of a triangle? |  |
| 2. Can Heron's Formula be applied to any type of triangle? |  |
| 3. How do you derive the semi-perimeter in Heron's Formula? |  |
| 4. What are some practical applications of Heron's Formula? |  |
| 5. Are there any limitations or restrictions when using Heron's Formula? |  |

|
Explore Courses for Class 9 exam
|

|





















