Class 9 Maths Chapter 2 HOTS Questions - Polynomials

Q.1. If  p(x) = x² – 2√2 x + 1, then find  p (2√2) .
Sol. Since, p(x) = x² – 2 √2 x + 1 , replacing value of x=2√2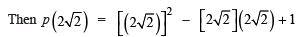

= 4 (2) – 4 (2) + 1

= 8 – 8 + 1 

= 1

Q.2. Factorize 3x²-14x - 5$2x^2\; +\; 7x\; +\; 3$using the middle term splitting method.
Sol.$\mathrm{ a}=3,b=-14,c=-\mathrm{5, }$We need two numbers that multiply to $ac=3\times (-5)=-15ac\; =\; 3\; \backslash times\; (-5)\; =\; -15$ and add up to $b=-14.=\; -14$

The numbers are -15 and 1 because $-15\times 1=-15-15\; \backslash times\; 1\; =\; -15$ and $-15+1=-14.-15\; +\; 1\; =\; -14$

Rewrite the middle term: $3x\mathrm{<sup\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">2</sup>}-15x+x-5$

$-\; 15x\; +\; x\; -\; 5$Factor by grouping:$(3x\mathrm{<sup\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">2</sup>}-15x)+(x-5)(3x^2\; -\; 15x)\; +\; (x\; -\; 5)$  ⇒ $3x(x-5)+1(x-5)3x(x\; -\; 5)\; +\; 1(x\; -\; 5)$  ⇒ $(3x+1)(x-5)(3x\; +\; 1)(x\; -\; 5)$(3x+1)(x−5)

So, the factorized form of $3x\mathrm{<sup\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">2</sup>}-14x-53x^2\; -\; 14x\; -\; 5$  is $(3x+1)(x-5)(3x\; +\; 1)(x\; -\; 5)$.

Q.3.Evaluate (102) ³  using suitable identity 
Sol. We can write 102 as 100+2
Using identity, (x+y) ³ = x ³ +y ³ +3xy(x+y)
(100+2) ³ =(100) ³ +2 ³ +(3×100×2)(100+2)
= 1000000 + 8 + 600(100 + 2)
= 1000000 + 8 + 60000 + 1200
= 1061208

Q.4.Factorise 4x² – 12x + 9 
Sol:To factorize this expression, we need to find two numbers α and β such that α + β = –12 and αβ = 36

4x² – 6x – 6x + 9

2x(x – 3) – 3(x – 3)

(2x – 3)(x – 3)

Q.5.Using the Factor Theorem to determine whether g(x) is a factor of p(x) in the following case p(x) = 2x³+x²–2x–1, g(x) = x+1
Sol. Given: p(x) = 2x³+x²–2x–1,  g(x) = x+1
g(x) = 0
⇒ x+1 = 0
⇒ x = −1
∴Zero of g(x) is -1.
Now,
p(−1) = 2(−1)³+(−1)²–2(−1)–1
= −2+1+2−1
= 0
∴ By the given factor theorem, g(x) is a factor of p(x).

Q.6.Expanding each of the following, using all the suitable identities:
(i) (x+2y+4z)²
(ii) (2x−y+z)²
Sol: (i) (x+2y+4z)²
Using identity, (x + y + z)² = x² + y² + z²+2xy + 2yz + 2zx
Here, x = x
y = 2y
z = 4z
(x + 2y + 4z)² = x² + (2y)² + (4z)²+(2 × x × 2y) + (2 × 2y × 4z) + (2 × 4z × x)
= x² + 4y² + 16z² + 4xy + 16yz + 8xz

(ii) (2x−y+z)²
Using identity, (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx
Here, x = 2x
y = −y
z = z
(2x − y + z)² = (2x)² + (−y)²+z²+(2 × 2x × −y)+(2 × −y × z)+(2 × z × 2x)
= 4x² + y² + z² – 4xy – 2yz + 4xz

Q.7. Factorize 12x²-29x +15using the middle term splitting method.
Sol. $a=12,b=-29,c=+15,$We need two numbers that multiply to $ac=12\times (15)=\; 180$ and add up to $b=-29.$
The numbers are -20 and -9 because $-20\times -9=180-20\; \backslash times\; -9\; =\; 180$ and $-20+-9=-29-20\; +\; -9\; =\; -29$.
Rewrite the middle term:12x²−20x−9x+15
Factor by grouping:(12x²−20x)+(−9x+15) $\mathrm{\Rightarrow \; 4}x(3x-5)-3(3x-5)4x(3x\; -\; 5)\; -\; 3(3x\; -\; 5)$ ⇒ (4x−3)(3x−5)
So, the factorized form of 12x²−29x+15 is $(4x-3)(3x-5)(4x\; -\; 3)(3x\; -\; 5)$.

Q.8.Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
(i) Area: 25a²–35a+12
(ii) Area: 35y²+13y–12
Sol: (i) Area: 25a²–35a+12
Using the splitting the middle term method,
We have to find a number whose sum = -35 and product =25 × 12 = 300
We get -15 and -20 as the numbers [-15 + -20 = -35 and -15 × -20 = 300]
25a²– 35a + 12 = 25a²– 15a − 20a + 12
= 5a(5a – 3) – 4(5a – 3)
= (5a – 4)(5a – 3)
Possible expression for length  = 5a – 4
Possible expression for breadth  = 5a – 3

(ii) Area: 35y²+13y–12
Using the splitting the middle term method,
We have to find a number whose sum = 13 and product = 35×-12 = 420
We get -15 and 28 as the numbers [-15+28 = 13 and -15×28=420]
35y² + 13y – 12 = 35y²–15y + 28y – 12
= 5y(7y – 3) + 4(7y – 3)
= (5y + 4)(7y – 3)
Possible expression for length  = (5y + 4)
Possible expression for breadth  = (7y – 3)

Q.10. Factorise 10y² – 28y + 14
Sol: To factorize this expression, we need to find two numbers α and β such that α + β = –28 and αβ = 140
10y² – 14y – 10y + 14
2y(5y – 7) – 2(5y – 7)
(2y – 2)(5y – 7)
2(y – 1)(5y – 7)