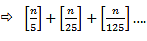How to Find Number of Trailing Zeros in a Factorial or Product | Quantitative for GMAT PDF Download
A Trailing zero is a zero digit in the representation of a number which has no non-zero digits that are less significant than the zero digit. Put more simply, it is a zero digit with no non-zero digits to the right of it.
 Representation of Trailing Zeros
Representation of Trailing Zeros
Trailing Zeroes of a Factorial
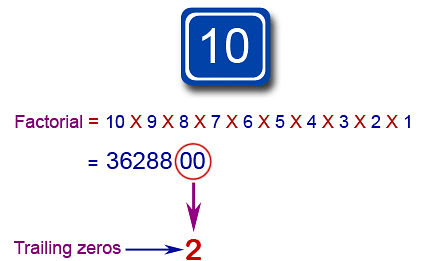
- If we take the factorial of any number larger than 5, then there will be at least one zero at the end of the number. Why? Because 5! = 1×2×3×4×5; in particular, 5! = (2×5)×(1×3×4), and (2×5) = 10.
- The factorial of any larger number will have more copies of 2 and 5 (as factors of larger values, like 6 and 15), so there will be even more factors of 10 in these factorials.
- And every factor of 10 adds a zero to the end of the factorial expansion.
Does Every Factorial Have at Least One Zero at the End
- Not every factorial has at least one zero at the end of it. However, as soon as you get to 5!, which contains a factor of 2 and a factor of 5, you'll get a trailing zero. Larger factorials will have more zeroes. So the only factorials which do not have any trailing zeroes are 0!, 1!, 2!, and 4!.
- This explains why there are trailing zeroes — because the factorials contain factors of 10 in them — but this doesn't tell us how to find the actual number of trailing zeroes. However, since the zeroes come from factors of 10, we can methodically figure out the actual number.
Steps for Finding a Factorial's Trailing Zeroes
1. Take the number that you've been given the factorial of.
2. Divide by 5; if you get a decimal, truncate to a whole number.
3. Divide by 52 = 25; if you get a decimal, truncate to a whole number.
4. Divide by 53 = 125; if you get a decimal, truncate to a whole number.
5. Continue with ever-higher powers of 5, until your division results in a number less than 1. Once the division is less than 1, stop.
6. Sum all the whole numbers that you got in your divisions. This is the number of trailing zeroes.
Number of Trailing Zeroes
(i) Number of trailing zeroes in a Product or Expression
- If we look at a number N, such that
N = 170130000 = 17013*104 - Number of trailing zeroes is the Power of 10 in the expression or in other words, the number of times N is divisible by 10.
- For a number to be divisible by 10, it should be divisible by 2 & 5.
- Consider a number N, such that
N = 2a * 5b * x
For the number to have a zero at the end, both a & b should be at least 1.
If you want to figure out the exact number of zeroes, you would have to check how many times the number N is divisible by 10.
When we divide N by 10, it will be limited by the powers of 2 or 5, whichever is lesser.
Number of trailing zeroes is going to be the power of 2 or 5, whichever is lesser.
Q1: What is number of trailing zeroes in 12000?
Ans: 12000 = 25 * 3 * 53
When I divide it by 10, it would be divisible exactly thrice because I have only three 5s.
In this case, number of 5s has become the limiting factor and so, the power of 5, which is 3 is the answer.
Tip: The power of 5 will be the limiting factor in most cases of continuous distribution. It will happen because 5 is less likely to occur than 2.
Q2: Find out the number of zeroes at the end of N?
Ans.: N = 11 * 22 * 33 .... .100100
Looking at the expression, we can say that the power of 5 will be the limiting factor.
All we need to do is to figure out the number of 5s in the expression.
11, 22, 33, 1717, 8989,… will not give us any 5s.
55 will give us five 5s.
1010 will give us ten 5s.
1515 will give us fifteen 5s.
And so on.
So, the total number of 5s that I have is
⇨ 5 + 10 + 15 ....100 = 5(1+2+3...20) = 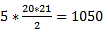
But I have made a mistake in the above calculation.
I have assumed that 2525 will give me twenty-five 5s but that is incorrect.
It is incorrect because 2525 = 550 and will actually give me 50 5s.
Other errors are:
5050 will actually give me 100 5s, whereas I have considered only 50 5s.
7575 will actually give me 150 5s, whereas I have considered only 75 5s.
100100 will actually give me 200 5s, whereas I have considered only 100 5s.
Considering the above, I have made an error of = 25 + 50 + 75 + 100 = 250 5s.
So the total number of 5s that I have are 1050 + 250 = 1300.
So the number of trailing zeroes at the end of the expression is 1300
(ii) Number of trailing zeroes in a factorial (n!)
- Number of trailing zeroes in n! = Number of times n! is divisible by 10 = Highest power of 10 which divides n! = Highest power of 5 in n!
The question can be put in any of the above ways but it can be answered using the simple formula given below:
{[x] is the greatest integer function. [4.99] = 4, [4.01] = 4, [- 4.99] = 5, [-4.01] = 5} - The above formula gives us the exact number of 5s in n! because it will take care of all multiples of 5 which are less than n. Not only that it will take care of all multiples of 25, 125, etc. (higher powers of 5).
Tip: Instead of dividing by 25, 125, etc. (higher powers of 5); it would be much faster if you divided by 5 recursively.
Q3: What is the number of trailing zeroes in 23!
Ans: [23/5] = 4. It is less than 5, so we stop here.
The answer is 4.
Q4: What is the number of trailing zeroes in 123!
Ans: [123/5] = 24
Now we can either divided 123 by 25 or the result in the above step i.e. 24 by 5.
[24/5] = 4. It is less than 5, so we stop here.
The answer is = 24 + 4 = 28
Q5: What is the number of trailing zeroes in 1123!?
Ans: [1123/5] = 224
[224/5] = 44
[44/5] = 8
[8/5]=1. It is less than 5, so we stop here.
The answer is = 224 + 44 + 8 + 1 =277
Finding Out 'N' When Number of Trailing Zeroes is Unkown
Q6: Number of trailing zeroes in n! is 13. n = ?
Ans: There is no standard formula for such type of questions but they can be solved by a little bit of hit and trial.
I need to get 13 trailing zeroes which I will definitely get from 65!
But it will have some extra zeroes in the end because of higher powers of 5.
So, I will consider the previous multiple of 5, which in this case is 60.
Trailing zeroes in 60! = [60/5] + [60/25] = 12 + 2 = 14
I got 14 but I want to get 13, so I will consider the previous multiple of 5, which in this case is 55.
Trailing zeroes in 55! = [55/5] + [55/25] = 11 + 2 = 13
So, the valid values of n! are 55!, 56!, 57!, 58!, 59!
Q7: Number of zeroes in n! is 23. n =?
Ans: Trailing zeroes in 100! = [100/5] + [100/25 ] = 20 + 4 = 24 {Too high. Consider previous multiple}
Trailing zeroes in 95! = [95/5] + [95/25] = 19 + 3 = 22 {Too low. Consider next multiple}
As you can see from above, we would end up in a loop.
This will happen because there is no valid value of n for which n! will have 23 zeroes in the end.
|
108 videos|103 docs|114 tests
|
FAQs on How to Find Number of Trailing Zeros in a Factorial or Product - Quantitative for GMAT
| 1. Does every factorial have at least one zero at the end? |  |
| 2. What are the steps for finding a factorial's trailing zeroes? |  |
| 3. How can I determine the number of trailing zeroes in a factorial? |  |
| 4. How do I find out 'N' when the number of trailing zeroes is unknown? |  |
| 5. Can you provide an example to illustrate how to find the number of trailing zeros in a factorial? |  |

|
Explore Courses for GMAT exam
|

|