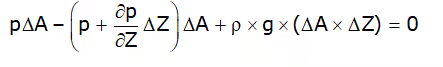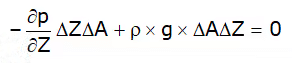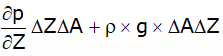Hydrostatic Forces on Surfaces | Fluid Mechanics for Mechanical Engineering PDF Download
Pascal’s Law
As per the Pascal's law, pressure or intensity of pressure at a point in a static fluid (fluid being in rest) is equal in all directions.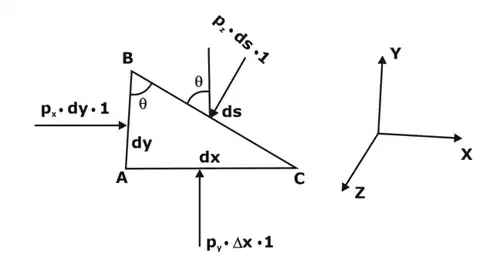 Showing a fluid element
Showing a fluid element
Consider an arbitrary fluid element of wedge shape having very small dimensions i.e. dx, dy and ds as shown in figure.
Let us assume the width of the element perpendicular to the plane of paper to be unity and let Px, Py and Pz be the pressure intensities acting on the face AB, AC and BC respectively.
Let ∠ ABC = θ. Then the forces acting on the element are:
- Pressure forces normal to the surfaces, and
- Weight of element in the vertical direction.
The forces on the faces are:
Force on the face AB = PX × Area of face AB
FAB = px × dy × 1 ………... (1)
Similarly, force on the face AC (FAC)= py × dx × 1 ……... (2)
Force on the face BC (FBC)= pz × ds × 1 ……. (3)
Element's weight = (Mass of element) × g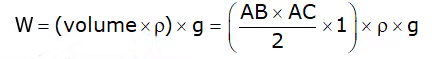
where ρ = density of fluid.
Resolving the forces in x-direction, we have
px × dy × 1 – pz (ds × 1) sin (90° – θ) = 0
px × dy × 1 – pz ds ×cos θ = 0 ……... (4)
But from fig.
ds cosθ = AB = dy ……. (5)
Thus, from equation (1) and (2):
∴ px × dy × 1 – pz × dy × 1 = 0
px = pz ………… (3)
Similarly, resolving the forces in y-direction, we get
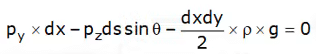
But ds sin θ = dx and the element is very small and hence dxdy will be negligible i.e. weight of fluid element can be neglected.
∴ pydx – pz × dx = 0
py = pz ……… (4)
From equations (3) and (4)
px = py = pz
The equation above illustrates that the pressure at any point in x, y, and z directions is equal. As the choice of the fluid element was completely random and arbitrary, it means that the pressure at any point is the same in all directions.
Examples:
Hydraulic lift, hydraulic break, etc.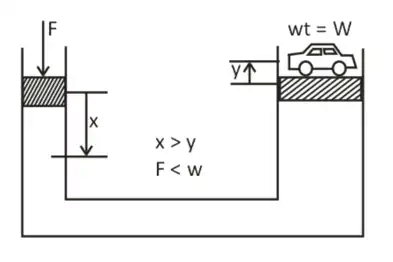 Hydraulic lift
Hydraulic lift
- In a hydraulic lift, a smaller force is required to lift a larger weight but still, the conservation of energy is not violated because the smaller force moves by a larger distance whereas larger wt. moves by smaller distance And hence work done in both the cases are same and hence conservation of energy is followed.
Hydrostatic Law
Pressure at any point in a fluid at rest is found out by the Hydro-static Law. As per this law, the rate of increase of pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point.
Consider a small fluid element as shown
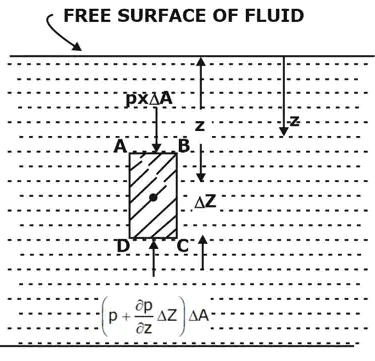 Forces on the fluid element
Forces on the fluid elementΔA = Cross-sectional area of element
ΔZ = Height of fluid element
p = Pressure on face AB
Z = Distance of fluid element measured from the free surface.
The forces acting on the fluid element are:
- Pressure force on AB = p × ΔA and acting perpendicular to face AB in the downward direction.
- Pressure force on

acting normal to face CD , vertically upward direction. - Weight of fluid element = Density × g × Volume = ρ × g × (ΔA × ΔZ).
- Pressure force on surfaces BC and AD are equal and opposite. For equilibrium of fluid element, we have



or ∂p/∂Z = ρ × g [cancelling ΔAΔZ on both sides]
∴ ∂p/∂Z = ρ × g ......(1)
where,
w = Weight density of fluid.
Equation (1) states that rate of increase of pressure in a vertical direction is equal to weight density of the fluid at that point. This is Hydrostatic Law.
Now, by integrating the above equation (1) for liquids: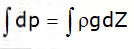
p = ρgZ ……… (2)
where p is the pressure above atmospheric pressure and Z is the height of the point from free surface.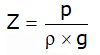
Here Z is called pressure head.
Note.2:
- Hydrostatic law can be applied to both compressible and incompressible fluids.
Pressure at a depth “h” Showing a point A location within the fluid
Showing a point A location within the fluid
Now use
∫dp = ∫ρgdh
P = ρgh + C …… (1)
At h = 0, P = Patm
Thus, C = Patm
P = ρgh + Patm ……… (2)
Therefore, PGauge = ρgh (N/m2 or Pascal)
Note 3:
- As we move vertically down is a fluid the pressure increase as +ρgh. As we move vertically up in a fluid the pressure decreases as –ρgh.
- There is no charge g pressure in the horizontally same level.
- For the conversion of one fluid column to another fluid column, we can use the following :
ρ1gh1 = ρ2gh2 valid for all fluids.
ρ1h1 = ρ2h2 valid for all fluids.
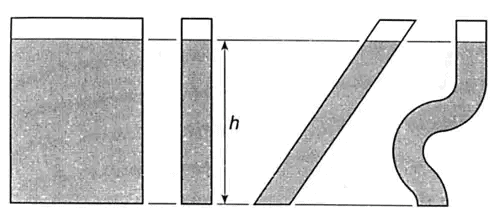
The Hydrostatic Paradox
- The pressure at any point depends only upon the depth below the free surface and the unit weight of the liquid.
The size and shape of the container do not affect the pressure exerted by the fluid. Hence, the pressure at the bottom of all containers will be the same if they are filled with the same liquid up to the same height. The hydrostatic paradox
The hydrostatic paradox
Hydrostatic Forces
- When a fluid, in contact with a surface is exerts a normal force on the surface, it is known as the hydrostatic force.
Hydrostatic forces on an inclined plane submerged surface in a liquid
Imagine a plane surface of any shape being immersed in a liquid in such a way that the plane surface makes an angle θ with the free surface of the liquid as shown in the figure below.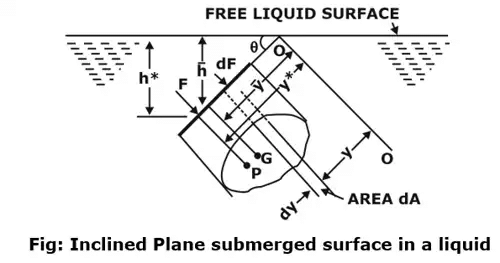
The force is given by: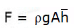
Hence, we can conclude that the force is independent of the angle of inclination (θ). Thus, the same expression could be used for the force calculation of Horizontal and vertical submerged bodies.
Centre of Pressure (h*):
It is the point where whole of the hydrostatic force is assumed to be acting.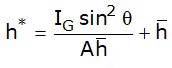
Plane vertical surface (θ = 90°)
Therefore, centre of pressure for a vertically submerged surface is given by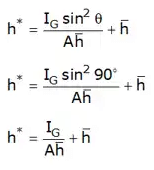
 Vertical submerged surface
Vertical submerged surface
Plane horizontal surface (θ = 0°)
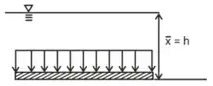 Horizontal submerged surface
Horizontal submerged surface
centre of pressure for the vertical submerged surface is given by:
Thus, the centre of pressure of a body submerged parallel to free surface will be equal to the distance of centroid of the body from the free surface.
Hydrostatic Forces on Curved Surfaces
 Hydrostatic force on a curved surface
Hydrostatic force on a curved surface
AC = curved surface
FY = vertical component of FR
FX = Horizontal component of FR
FR = Resultant force on a curved surface.
The horizontal component of force on a curved surface:
The horizontal component of force acting on a curved surface equals the hydrostatic force on the vertical projected area of the curved surface.
Horizontal force:
Where,
A = Projected Area = depth of centroid of an area.
= depth of centroid of an area.
This force acts at the center of the pressure of the corresponding area.
The vertical component of force on a curved surface
- The vertical component of the hydrostatic force on a curved surface is given by the weight of the fluid contained by the curved surface up to the free surface of the liquid.
- It will act at the center of gravity of the volume of liquid contained in a portion extended above the curved surface up to the free surface of the liquid.
|
56 videos|104 docs|75 tests
|
FAQs on Hydrostatic Forces on Surfaces - Fluid Mechanics for Mechanical Engineering
| 1. What is hydrostatic force on a surface? |  |
| 2. How is the hydrostatic force calculated on a submerged surface? |  |
| 3. What factors affect the magnitude of hydrostatic force on a surface? |  |
| 4. How does the shape of a submerged surface affect the hydrostatic force? |  |
| 5. Can hydrostatic force cause structural failure? |  |
|
56 videos|104 docs|75 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|