Ideal Gas Laws: Revision Notes | Physical Chemistry PDF Download
| Table of contents |

|
| Gaseous State |

|
| Measurable Properties of Gases |

|
| The Gas Laws |

|
| Ideal Gas Equation |

|
| Dalton’s Law of Partial Pressures: |

|
| Graham’s Law of Diffusion |

|
Gaseous State
In the gaseous state, the molecules are farthest apart as compared to solid and liquid states and the intermolecular forces are negligible so the particles move randomly.
A given substance may occur in solid, liquid or gaseous phase depending upon the relative value of two tendencies namely Mutual Attraction (MA) and Escaping Tendency (ET)
If MA is greater than ET then substance will occur in solid state.
If MA is slightly greater than ET then substance will occur in liquid state.
If MA is very much less than ET then substance will occur in gaseous state
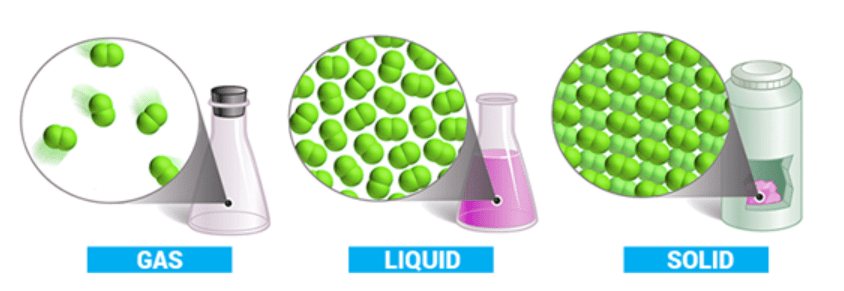
Out of the three states of matter, the most simplest one is the gaseous state.
- The state is characterized by sensitivity of volume change with change of pressure and temperature.
- It is due to large distance between molecules as compared to their own dimensions.
- There exist weak Vander Waal’s forces, molecules move independently of each other with speed about 400 ms–1.
Gases show maximum equality in their behavior irrespective of their nature.
Measurable Properties of Gases
Mass
The gases possess mass. The mass of gas is generally used in the of form of number of moles which is related as
(i) no. of moles =
Two other useful formulae to calculate number of moles of gas are
(ii) number of moles =
(iii) no. of moles =
When a container contains more than one gas then the molecular mass of mixture is termed as effective molecular mass (EMM) which is intermediate between molecular masses of all the gases present in the container.
Effective molecular mass =
Volume
Volume of gas is nothing but volume of the container in which it is present.
Relation between different units of volume
1m3 = 103 dm3 = 103 litre = 106 cm3 = 106 ml = 109 mm3
Temperature
Degree of hotness or coldness of a body is measured by temperature
C – Celcium scale, K – Kelvin scale,F – Fahrenheit scale
Pressure
Force acting per unit area
Unit:
CGS : dyne/cm2
MKS : Newton/m2 (1N/m2 = 1 Pa)
Relation : 1N/m2 = 10 dyne/cm2
Units of pressure:
1 atm = 76 cm of Hg
= 760 mm of Hg
= 760 torr
= 1.01325 × 105 N/m2
= 101.325 kPa
= 1.01325 bar
= 14.7 lb/In2 (Psi)
= 10.33 meters of H2O
Density
Mass per unit volume
Units:
CGS= g/cm3
MKS = kg/m3
Relation : 1 kg/m3 = 10–3 g/cm3
Absolute density (mass per unit volume) | Relative density (Relative to hydrogen turned as vapour density) |
(i) | |
(ii) unit : g/l | (ii) No unit |
(iii) Function of temperature, pressure no. of moles | (iii) Independent of Pressure, Temperature |
Note: Mass, volume and number of moles are extensive properties that depend on mass hence then all divertly additive
Note: Density, Pressure and Temperature are intensive properties they does not depend on mass hence they are non-additive in nature.
The Gas Laws
Boyle’s Law:
It relates the volume and the pressure of a given mass of a gas at constant temperature. Boyle’s law states that, “at constant temperature, the volume of a sample of a gas varies inversely with the pressure.”
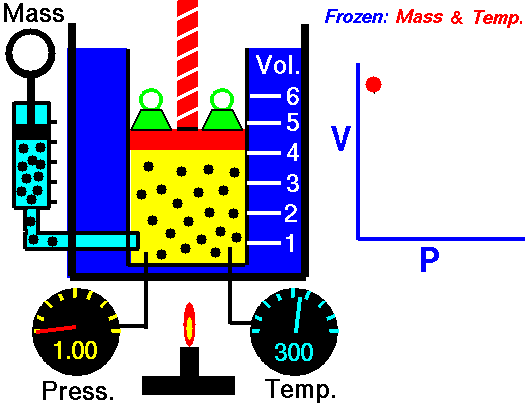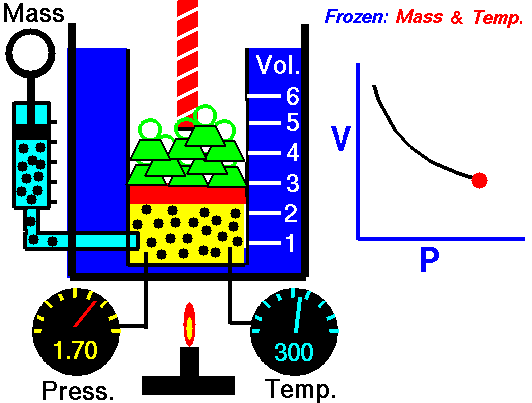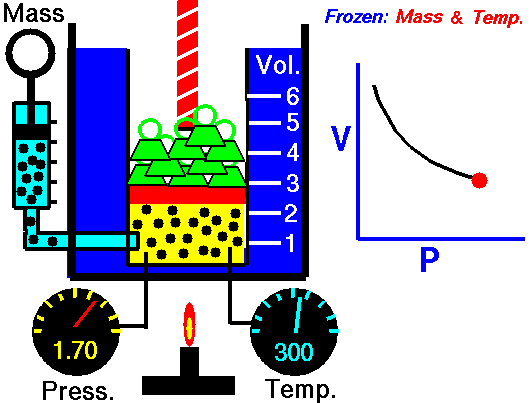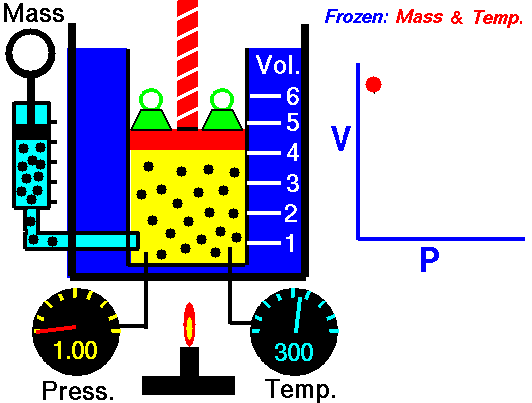
∴ (when temperature and number of moles are kept constant)
The proportionality can be changed into an equality by introducing a constant k, i.e.,
Boyle’s law can be verified by any one of the following three ways graphically.
Alternatively, Boyle’s law can also be stated as follows:
“Temperature remaining constant, the product of pressure and volume of a given mass of a gas is constant”. The value of the constant depends upon the amount of a gas and the temperature.
Mathematically, it can be written, as,
P1V1 = P2V2 = P3V3 = ………………..
Location of straight line and curve change with temperature in the isotherm shown in the following figure.
According to Boyle’s law, PV = Constant at constant temperature
∴
Charles’ Law:
It relates the volume and temperature of a gives mass of gas at constant pressure.
For each degree change of temperature, the volume of a sample changes by the fraction
of its volume at 0°C.
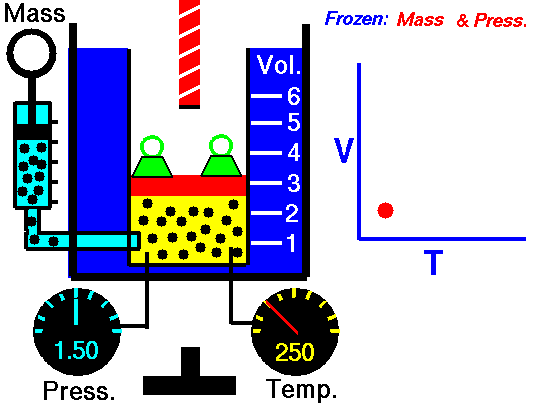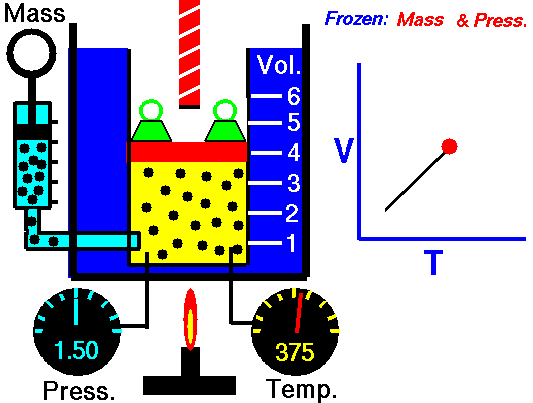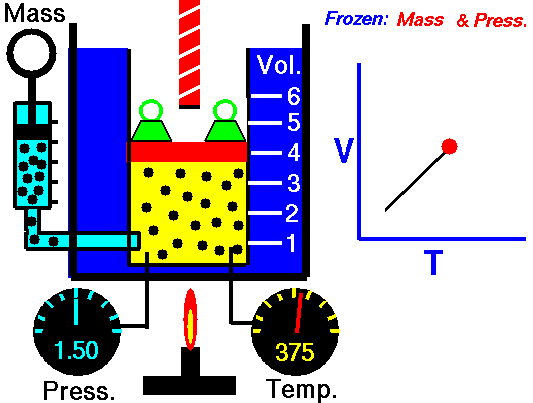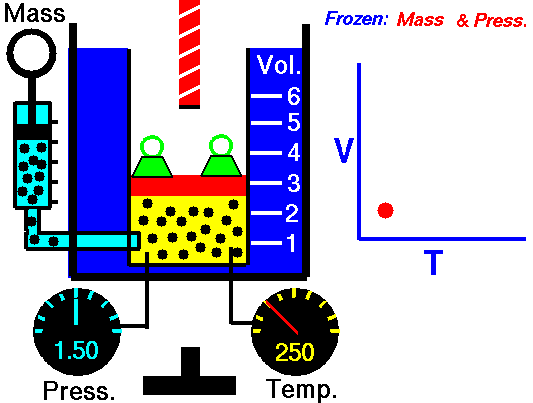
Let the volume of a given amount of gas be V0 at 0°C. The temperature is increased by t°C and the new volume becomes Vt
Thus,
A new temperature scale was introduced known as Kelvin scale or absolute scale (named after the British physicist and mathematician Lord Kelvin). The lower limit of the scale is called absolute zero which corresponds to –273°C.
At absolute zero or –273°C, all molecular motions would stop and the volume of the gas would become zero. The temperature in absolute scale is always obtained by adding 273 to the temperature expressed in °C.
K = (t°C + 273)
This new temperature scale may be used for deducing Charles’ law.
By substituting T for 273 + t and T0 for 273 in Eq. (i).
or
Or pressure is kept constant
Alternatively, Charles’ law can be stated as follows:
“The volume of a given amount of a gas at constant pressure varies directly as its absolute temperature”.
(if pressure is kept constant)
Pressure-Temperature Law: (Gaylussac’s Law)
It relates the pressure and absolute temperature of a given mass of a gas at constant volume.
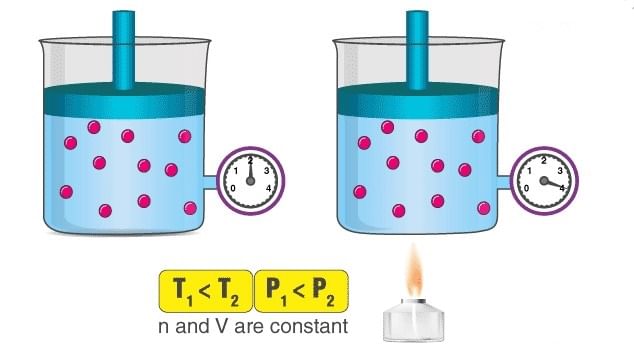 An illustration describing the increase in pressure that accompanies an increase in the absolute temperature of a gas kept at a constant volume is provided above. Volumes remaining constant, the pressure of given mass of a gas increases or decreases by
An illustration describing the increase in pressure that accompanies an increase in the absolute temperature of a gas kept at a constant volume is provided above. Volumes remaining constant, the pressure of given mass of a gas increases or decreases by of its pressure at 0°C per degree change of temperature.
(if volume and number of moles are kept constant)
At constant volume, the pressure of a given amount of a gas is directly proportional to its absolute temperature.
Avogadro’s Law
(i) For Solid, liquid and gas
1 mole of any substance contains Avogadro’s number (NA) of molecules/atoms/particles etc.
NA = 6.023 × 1023
(ii) For gases:
In 1812, Amadeo Avogadro stated that samples of different gases which contain the same number of molecules (any complexity, size, shape) occupy the same volume at the same temperature and pressure. It follows from Avogadro’s hypothesis that v ∝ n (T and P are constant)
v ∝ n (T, P constant) =
STP: 273.15 K 1 atm
SATP: 298.15 K 1 bar
Ideal Gas Equation
Combining all these gas laws, a simple equation can be derived at, which related P, V, n and T for a gas
PV = nRT (for n moles of gas)
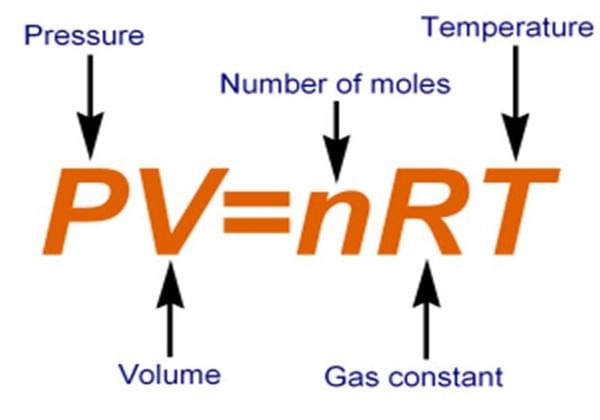
(Combined gas law)
P is the pressure of the gas and can be expressed in atm of Pa. Correspondingly, the volume must be expressed in litres or m3 respectively. n is the number of moles and T is the temperature in Kelvin. R is called the universal gas constant.
Numerical Values of R
(i) In litre atmosphere = 0.0821 litre atm deg–1 mole–1
(ii) In ergs = 8.314 × 107 erg deg–1 mole–1
(iii) In jouls = 8.314 jouls deg–1 mole–1
(iv) In calories = 1.937 cal deg–1 mole–1
Relation between Molecular Mass and Gas Densities
Actual density: For an ideal gas PV = nRT or
where w = mass of the gas in gms and
M = Molecular wt. in gms.
∴ or
=
∴
(i)
(ii)
(where d = density of gas)
Vapour Density: for gases another term which is often used is vapour-density. Vapour density of a gas is defined as the ratio of the mass of the gas occupying a certain volume at a certain temperature and pressure to the mass of hydrogen occupying the same volume at the same temperature and pressure i.e. W
.
(Vapour density of gas)
Vapour density of a gas is same at any temperature, pressure and volume.
Dalton’s Law of Partial Pressures:
The total pressure of a mixture of non-reacting gases is equal to the sum of their partial pressures.
By Dalton’s Law PT = P1 + P2 + ………………..
By the partial pressure of a gas in a mixture is meant, the pressure that the gas will exert if it occupies alone the total volume of the mixture at the same temperature.
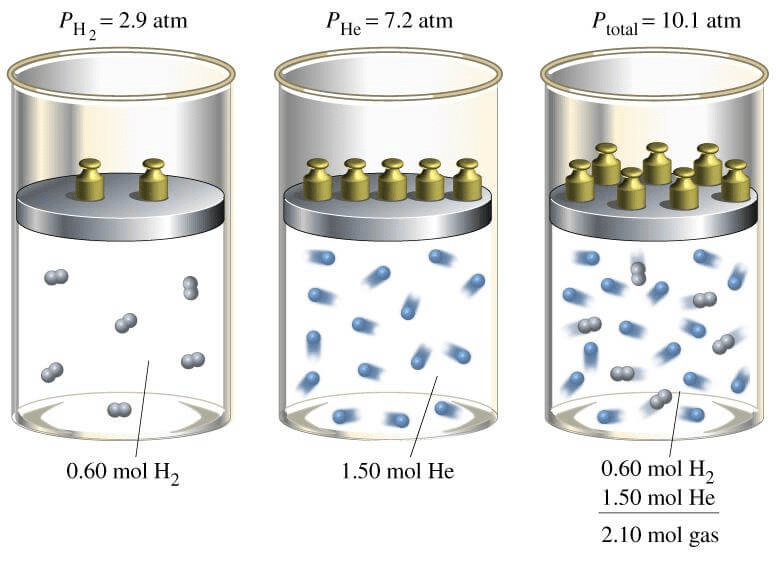
Derivation: n = n1 + n2 + ……………..
Assumption: Volume of all the gases is same as they are kept in same container.
Relationship between Partial Pressure and Number of Moles
Important formula
(i)
(ii) Partial pressure of gas in the mixture =
Partial pressure and Aqueous Tension
Dalton’s law is used to calculate the pressure of a dry gas when it is collected over water at atmospheric pressure.
By Dalton’s law,
Graham’s Law of Diffusion
Diffusion is the tendency of any substance to spread throughout the space available to it. Diffusion will take place in all direction and even against gravity.
The steaming of gas molecules through a small hole is called effusion.
According to Graham, the rate of diffusion (or effusion) of a gas at constant pressure and temperature is inversely proportional to the square root of its molecular mass.
, at constant P and T
at constant P and T
Since molecular mass of gas = 2 × vapour density, at constant P and T
The rate of diffusion (or effusion) r of two gases under different pressure can be given by
at constant T only.
Therefore, according to Graham’s law of diffusion (effusion) at constant P and T.
d1 and d2 are the respective densities and V1 and V2 are volumes diffused (effused) in time t1 and t2.
Where n1, n2 are modes diffused (effused) in time t1 and t2
Where x1 and x2 are distances travelled by molecules in a narrow tube in time t1 and t2.
|
84 videos|142 docs|67 tests
|
FAQs on Ideal Gas Laws: Revision Notes - Physical Chemistry
| 1. What are the measurable properties of gases? |  |
| 2. What are the gas laws? |  |
| 3. What is the ideal gas equation? |  |
| 4. What is Dalton's law of partial pressures? |  |
| 5. What is Graham's law of diffusion? |  |
















