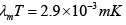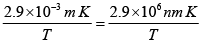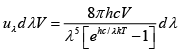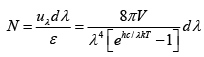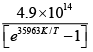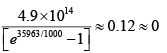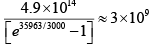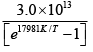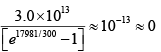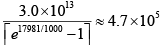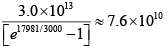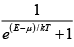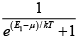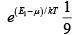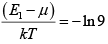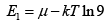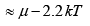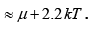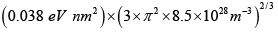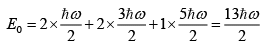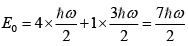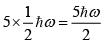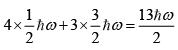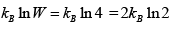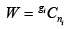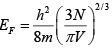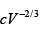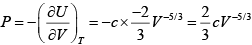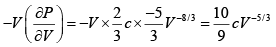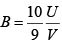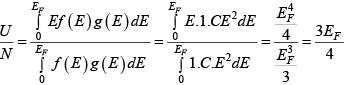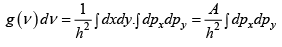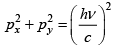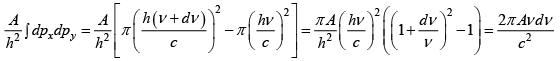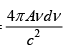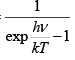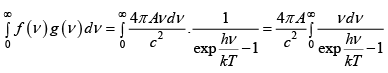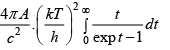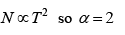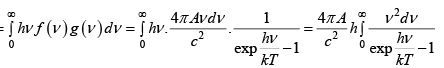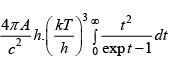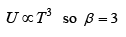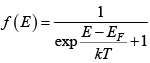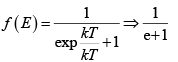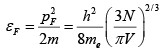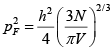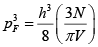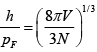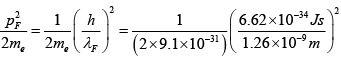Identical Particle: Assignment | Kinetic Theory & Thermodynamics - Physics PDF Download
Q.1. Compare the rate of fall of temperature of two solid sphere of the same material and similar surfaces, where the radius of one surface is four times and the Kelvin temperature of the large sphere is twice that of the small one. (assume that the temperature of the sphere is so high that absorption from the surrounding may be ignored).
P = 4πR2σT4
P =
=
where s is specific heat
= 4
Q.2. Three identical Boson particles are to be distributed in three Quantum states. (a) Make a detailed pictorial representation showing a stage by a horizontal line and a particle by a dot for each possible way of distribution. (b) How many possible arrangements are there? (c) Use the method of permuting vertical lines and dots to find the number of possible arrangements. (d) What is the probability that all three particles occupy the same
quantum state?
(a)
all three together
two in one state and one in other
all in different states
(b) 10
c) There are three vertical lines for three quantum states, and three dots for the particles. The first vertical line remains undisturbed. The rest five symbols can be permuted in 5! ways. The two vertical lines can be permuted 2! ways and the three dots can be permuted 3! ways. These permutations are not be counted separately. So the number of possible arrangements is
= 10
Look at the solution of part (a), there are 3 ways. out of a total of 10 , in which all the particles can occupy the same state. Assuming all arrangements to be equally probable, the probability of all three occupying the same state is 3 / 10 .
Q.3. Find the wavelength λm corresponding to the maximum energy density for blackbody radiation at (a) 300K (b) 2000K and (c) 5000K .
From Wien's displacements law,
or λm =
(a) T = 300K . So, λm =
= 9670nm
(b) T = 2000K . So, λm =
= 1450nm
(c) T = 5000K . So, λm =
= 580nm
Q.4. Estimate the number photons with wavelength in the range 400 to 405nm in a cavity of volume 100cc at (a) 300K , (b) 1000K (c) 3000 K .
The energy of the radiation in the wavelength λ to λ + dλ is given by
The energy of a photon with wavelength λ is ε = hc /λ . As dλ is small, the number of photons with wavelength λ to λ + dλ is
As you know, hc = 1240 eV nm and k = 8.62´10-5 eV / K
So N =
=
(a) T = 300K, N =
(b) T = 1000K, N =
(c) T = 3000K, N =
Q.5. Estimate the number of photons with wavelength in the range 800and 805nm in a cavity of volume 100 cc at (a) 300K , (b) 1000K (c) 3000K
N =
=
(a) T = 300K, N =
(b) T = 1000K, N =
(c) T = 3000K, N =
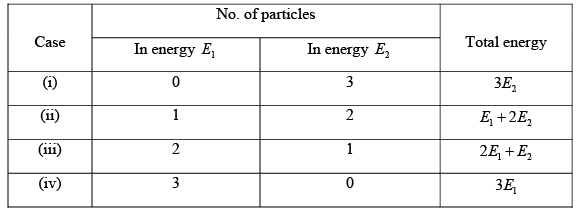
Q.6. Three identical Fermions particles are to be distributed in two energy levels 1 E and 2 E . Each of the two energy levels is 5 -fold degenerate. (a) What are the possible values of the total energy of three particles? (b) for each such possible total energy, find the number of ways in which the particles can be distributed. (c) what is the total number of ways in which the particles can be distributed?
(a) Since each of the energy level is 5 -fold degenerate, any number of particle, out of three given, can be put in any of the energy level. We show below the differential ways of distributing these three particles in the two energy levels and the total energy corresponding to each such distribution.
(b) In case (i), the three particles are to be distributed in 5 quantum states. This can be done in 5C3 = 510 ways.
In case (ii) one particle is to be put in one of the 5 quantum states of energy E1 , and two particles are to be put in the 5 quantum states of energy of E2 . One particle can be put in 5 state in 5C1 = 5 ways and two particles in 5 state can be put in 5C2 = 10 ways. So the distribution in case (ii) cab be done in 5C1 x 5C1= 50 ways.
(c) The total number of ways in which particles can be arranged is 10 + 50 + 50 +10 = 120
You can also get it directly from the fact that we have distributed 3 Fermions in 10 quantum states and that can be done in 10C3 = 120 .
Q.7. The Fermi level for a system of identical Fermions is μ . Find the energy at which the distribution function f (E) is (a) 0.90 (b) 0.10
The distribution function is f(E) =
(a) let the energy be E1 where value of f (E ) is 0.90 . Then,
0.9 =
or,
or,
or,
(b) Let the energy be E2 when this probability is 0.10 , then,
0.1 =
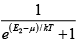
This gives,
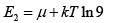
Q.8. Copper contains 8.5 x 1028 free electrons per cubic meter. Assuming free electron model, calculate the Fermi energy for these electrons.
=
=
Q.9. Consider a one-dimensional harmonic oscillator of angular frequencyε . If 5 identical particles occupy the energy levels of this oscillator at zero temperature. Answer the following questions.
(a) If the particles are electrons what is ground state energy of system?
(b) If the particles are fermions of spin 3/2, what is ground state energy of system?
(c) If the particles are spin-less fermions, what is ground state energy of system?
(d) If the particles are bosons what is ground state energy of system?
(a) If particles are electrons then spin is 1/2 then ground state energy
(b) If particles are fermions with spin is 3/2 then ground state energy
(c) If the particles are spin-less fermions, then energy is
(d) If the particles are bosons E0=
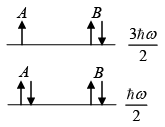
Q.10. Let A and B represent two types of non-interacting spin-1/2 particles. If 3 particles of type A and 4 particles of type B are in a simple harmonic oscillator potential characterized by ω, then what is ground state energy of the system.
Q.11. Consider a system of 3 particle which can occupy any of the 4 available energy states with equal probability. Then Find the entropy of the system.
(a) If particles are fermions without spin
(b) If particle are fermions with spin 1/2
(c) Particles are Bosons
(d) If particle are classical distinguishable
(a) ni = 3, gi = 4
Number of ways that 3 fermions will adjust in 4 available energy is
So entropy is S =
(b) In case of fermions with spin s = 1/2, ni = 3, so multiplicity is 2s +1= 2 then gi = 4 x2=8
Number of ways that 3 fermions will adjust in 8 available energy is
= 56
so entropy is S = kBInW = kBIn56
(c) In case of boson ni =3, gi = 4
W =
= 20
S = kBInW = kBIn20
(d) In case of distinguishable particle
N = 3 , ni =3, gi = 4
W =
⇒
= 43 = 64
S = kBInW = kBIn64
Q.12. If fermions are confine in Volume V at equilibrium temperature T = 0K .if U is internal energy of system prove that Bulk modulus 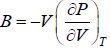 is given by
is given by 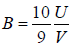 .
.
∵
U =
=
dU = TdS- PdV ∵
Hence Bulk modulus, B =
,
Q.13. If fermions of rest mass m are moving with relativistic speed such that pc = mc2 in volume V at equilibrium temperature T = 0K , then Find the average energy .
Fermions at temperature T = 0K
For three dimensional case g ( E ) ∝ E2 ⇒ g ( E ) = CE2 relativistic
(U) =
Q.14. (a) In case of photon find density of quantum state between v and dv in two
dimensional area A
(b) If number of photon is proportional to Tα then find value of α .
(c) If energy of photon is proportional to T β then find value of β
(a)
If polarization is included then g(v) dv =
(b) f(v) =
N =
=
(c) U =
=
Q.15. Calculate the probability that an allowed state is occupied if it is lied above Fermi level by kT .
It is given E - EF= kT
Q.16. Calculate the Fermi wavelength and Fermi energy for 4.2x1021 electrons in box of volume 1cm3 .
From Fermi Energy:
⇒
On raising the power of both sides by 3 / 2 , we can write
⇒
Hence, Fermi wavelength λF =
On substituting the given values, we get
λF =
= 1.52 x 10-19 J
|
6 videos|20 docs|32 tests
|
FAQs on Identical Particle: Assignment - Kinetic Theory & Thermodynamics - Physics
| 1. What is the concept of identical particles in physics? |  |
| 2. How does the concept of identical particles relate to the IIT JAM exam? |  |
| 3. What are the different types of identical particles? |  |
| 4. How are identical particles different from distinguishable particles? |  |
| 5. What are some applications of identical particles in physics? |  |