Imperfect and Perfect Differentials | Basic Physics for IIT JAM PDF Download
Thermodynamics is the study of stable equilibrium in macroscopic systems. The terms “macroscopic” and “stable equilibrium” require some definition:
Macroscopic system
For a system constituted of N particles, 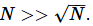 Fluctuations must be small compared to mean, and this can happen only for large particle numbers. During the inception of thermodynamics in the 19th century, this criterion was not understood because systems were assumed to be continuous, i.e. not made of of vast numbers of exceedingly small particles. Derivation of the inequality used in this definition will have to await our study of statistical mechanics, which acknowledges the particulate nature of matter.
Fluctuations must be small compared to mean, and this can happen only for large particle numbers. During the inception of thermodynamics in the 19th century, this criterion was not understood because systems were assumed to be continuous, i.e. not made of of vast numbers of exceedingly small particles. Derivation of the inequality used in this definition will have to await our study of statistical mechanics, which acknowledges the particulate nature of matter.
Stable Equilibrium
Stable equilibrium occurs when all macroscopic observables for a system are constant, no new mass-energy flow occurs, and the system returns to its initial state after small perturbation is removed.
In reality this is always an approximation valid only for a finite time because any system (except maybe the whole universe!) is eventually subject to external influences such that one or more of the three requirements above are no longer met. In particular, thermodynamics is not about the type of equilibrium where a system is teetering on the edge, like a ball poised at the top of a conical hill. Stability implies systems analogous to a ball at the bottom of a conical lake.
Systems where thermodynamics does not apply:
- Very few signaling molecules in a cell (N too small)
- Critical point (fluctuations no longer
 )
) - Open flame (mass-energy flow occurs even in steady-state)
Systems where thermodynamics applies well:
- A pH 3, mM solution of protein
- A completed reaction in a calorimeter.
Even in cases where thermodynamics does not apply, it can put useful constraints on possible states of the system. These constraints can be extremely firm, because they are based on a few very simple assumptions only. Hence Einstein’s claim that the second law is not likely to be overthrown anytime soon. The power of thermodynamics is often not in what it says can happen, but in what it says cannot happen.
Here we will discuss thermodynamics on a formal basis, beginning with the definition of several concepts that we will manipulate, with the aid of some axioms, or “postulates of thermodynamics.” Everything follows uniquely from these postulates. One important thing to keep in mind is that thermodynamics makes statements about macroscopic variables (those with well-defined values in macroscopic systems) while making almost no prior assumptions about the system. Thermodynamics cannot be used to derive a fundamental relation that tells us everything about the macroscopic variables; for that, we need the Hamiltonian of the system and statistical mechanics. Thermodynamics can take fundamental relations of a system, and give us the values of almost any macroscopic variable we want, and connections among the variables, – as long as the system remains at equilibrium. Thermodynamics can also tell us which equilibrium state can go to another, even more favorable equilibrium state, but not vice-versa. For example, given a single fundamental relationship among variables such as V,T and N for an ideal gas (it’s not PV = NRT by the way), thermodynamics can tell us anything we want about the connection among variables such as the above, or U (internal energy), or α (thermal expansion coefficient), or any other relevant macroscopic variable. It can also tell us that a state with P = 1 atm, V = 1 liter, T = 298 K can spontaneously evolve to the state P = 0.5 atm, V=2 liters, T = 298 K, when a barrier dividing a box in half is removed, but not vice-versa when the barrier is re-inserted.
Some definitions
- Simple system: A spatially and temporally homogeneous system, labeled {S}.
- Constraints: Constraints or “walls” are used to (arbitrarily) partition a system into subsystems. The constraints may prevent heat flow (adiabatic) or allow it (diathermal); they may prevent mass flow (impermeable) or allow it (permeable); they may prevent volume changes (rigid) or allow them (flexible).
The main task of thermodynamics is to calculate new equilibrium states when a constraint has been removed, and relate all the macroscopic variables in these states.
- Composite systems: A system composed of subsystems separated by constraints. (The subsystems may be simple or composite themselves):

- Closed system: A system all of whose macroscopic observables (e.g. mass-energy, volume, mole numbers, etc.) are constrained. (i.e. it lies within a diathermal, inflexible, impermeable, etc. wall).
Note that many thermodynamics texts actually call this an ‘isolated system,’ and reserve ‘closed’ for a system surrounded by an impermeable wall. Classical or quantum dynamics texts invariably use the definition given here because the distinction of mass and energy flow is ultimately futile. According to the special theory of relativity, a system that loses energy in an exothermic reaction in fact also loses mass. If it is a nuclear reaction, even a quite noticeable amount of mass. We will make a connection between thermodynamics and dynamics via statistical mechanics, and so we will use the mechanical definition of the term ‘closed,’ and not use the term ‘isolated system’ at all.
- Open system: one that is not closed.
A very important point: The thermodynamics postulates we will soon encounter apply only to closed systems. If we want to deal with open systems, we have to embed them in a closed system first, as shown in the figure below. We then derive statements about the open system of interest by applying thermodynamics to the composite closed system consisting of “open system” and “environment.”
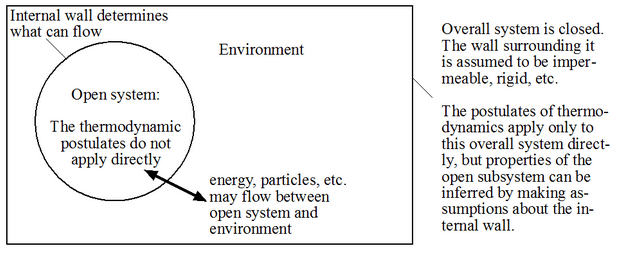
- Reservoirs or baths: A particularly useful composite system consists of a closed system within which there is an open system coupled to a reservoir or “bath”:
The idea is that the “bath” is so large that its properties are affected very little while the open system reaches equilibrium. The walls separating the open system and the bath can be diathermal (heat bath), flexible (constant pressure bath), etc. Although some chemical transformations can be described using simple closed systems (e.g. bomb calorimeter), most are better described by an open system. Putting this open system within a large closed system allows us to still apply the postulated the thermodynamics. If the nature of the constraints between the open system and the bath is well understood, much information about the open system can be obtained once equilibrium has been reached.
- Extensive variables X are additive for a composite system:
 (1)
(1)
Examples 1.1

In the case where the composite system is an “ensemble” or a scaled version of a system 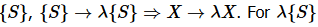 to correspond to an ensemble of systems
to correspond to an ensemble of systems 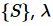 , has to be a natural number.
, has to be a natural number.
Intensive variables: Iij are scale invariant for a simple system. Let Ni and Nj be two extensive variables, then
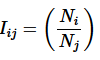 (2)
(2)
is intensive: as
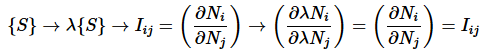 (3)
(3)
Example 1.2
 (4)
(4)
 (5)
(5)
Perfect and imperfect differentials: State functions
For a macroscopic variable to be well-defined in a given equilibrium state, it must be unique to that state. To phrase this somewhat tautological statement a bit differently: as we observe a system and see that it has different equilibrium states, only variables that always retain the same value for a given state are useful for labeling that state.
Let 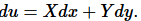 Does a function u exist? If u exists, the functions X and Y cannot be arbitrary functions:
Does a function u exist? If u exists, the functions X and Y cannot be arbitrary functions:
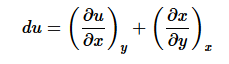 (6)
(6)
 (7)
(7)
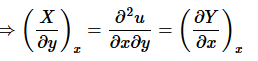 (8)
(8)
The function u exists if and only if
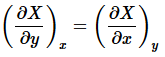 (9)
(9)
then 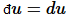 is a perfect (also known as exact) differential. Otherwise du
is a perfect (also known as exact) differential. Otherwise du
is imperfect (also known as inexact).
This has important implication for thermodynamics, especially for state functions. Let x and y describe the state a system. For a closed loop 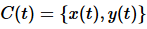 it follows that
it follows that
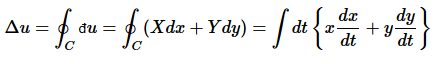 (10)
(10)
But if u = u(x,y) exists, then
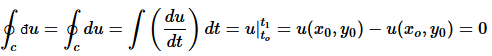 (11)
(11)
Thus, perfect differentials belong to the state functions, which are uniquely defined for a given state. Of course, any perfect differential can be broken up into imperfect differentials: 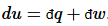 . In thermodynamics, the most useful division is into heat flow and work:
. In thermodynamics, the most useful division is into heat flow and work:
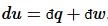 (12)
(12)
The distinction between heat and work is a practical one: the energy put into the system or removed from the system via manipulation of the few extensive variables or “degrees of freedom” we can control is called “work.” For example, a force may displace the system so 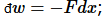 ; or a pressure may change a volume, so
; or a pressure may change a volume, so 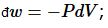 or an electric field may induce a dipole, so
or an electric field may induce a dipole, so .
.

The rest of the energy flow is “heat.” (Generally, few means << 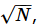 usually O(1)). If we learn to control an additional degree of freedom that could previously not be manipulated, its energy flow then becomes “work.” A misunderstanding of this fact has led to many fruitless discussions about “Maxwell’s demons” and similar things in the thermodynamic literature, and what they are supposed to be able to do, and what not. It is in fact perfectly possible in principle to build a “demon” that will open a door to let molecules from one chamber into another, eventually creating a vacuum in the first chamber, reversing a process of random expansion. One needs to just look at the STM pictures of individual atoms arranged into letters by lifting them with a tip to realize that this sort of thing must be doable. It’s just that the demon will have to cause an increase in entropy elsewhere to offset such a major decrease in entropy of the system it controls, as required by the second postulate (or “law”) of thermodynamics. Furthermore, if we have no direct control over most degrees of freedom, we cannot convert them with complete efficiency into the few manipulable ones, meaning we cannot turn heat into work with 100% efficiency. This brings us to the formulation of the postulates of thermodynamics, which determine exactly what can and cannot be done.
usually O(1)). If we learn to control an additional degree of freedom that could previously not be manipulated, its energy flow then becomes “work.” A misunderstanding of this fact has led to many fruitless discussions about “Maxwell’s demons” and similar things in the thermodynamic literature, and what they are supposed to be able to do, and what not. It is in fact perfectly possible in principle to build a “demon” that will open a door to let molecules from one chamber into another, eventually creating a vacuum in the first chamber, reversing a process of random expansion. One needs to just look at the STM pictures of individual atoms arranged into letters by lifting them with a tip to realize that this sort of thing must be doable. It’s just that the demon will have to cause an increase in entropy elsewhere to offset such a major decrease in entropy of the system it controls, as required by the second postulate (or “law”) of thermodynamics. Furthermore, if we have no direct control over most degrees of freedom, we cannot convert them with complete efficiency into the few manipulable ones, meaning we cannot turn heat into work with 100% efficiency. This brings us to the formulation of the postulates of thermodynamics, which determine exactly what can and cannot be done.
|
210 videos|156 docs|94 tests
|
FAQs on Imperfect and Perfect Differentials - Basic Physics for IIT JAM
| 1. What is an imperfect differential? |  |
| 2. What is a perfect differential? |  |
| 3. What is the significance of the difference between imperfect and perfect differentials? |  |
| 4. Can an imperfect differential be converted into a perfect differential? |  |
| 5. How are imperfect and perfect differentials used in thermodynamics? |  |

|
Explore Courses for Physics exam
|

|
 )
)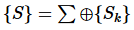
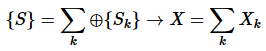 (1)
(1)

















