Importance of Effective Stress | Soil Mechanics - Civil Engineering (CE) PDF Download
The Importance of Effective Stress
At any point within the soil mass, the magitudes of both total stress and pore water pressure are dependent on the ground water position. With a shift in the water table due to seasonal fluctuations, there is a resulting change in the distribution in pore water pressure with depth.
Changes in water level below ground result in changes in effective stresses below the water table. A rise increases the pore water pressure at all elevations thus causing a decrease in effective stress. In contrast, a fall in the water table produces an increase in the effective stress.
Changes in water level above ground do not cause changes in effective stresses in the ground below. A rise above ground surface increases both the total stress and the pore water pressure by the same amount, and consequently effective stress is not altered.
In some analyses it is better to work with the changes of quantity, rather than in absolute quantities. The effective stress expression then becomes:
Ds´ = Ds - Du
If both total stress and pore water pressure change by the same amount, the effective stress remains constant.
Total and effective stresses must be distinguishable in all calculations.Ground movements and instabilities can be caused by changes in total stress, such as caused by loading by foundations and unloading due to excavations. They can also be caused by changes in pore water pressures, such as failure of slopes after rainfall.
Example 1; For the soil deposit shown below, draw the total stress, pore water pressure and effective stress diagrams.The water table is at ground level.
Solution:
Total stress
Pore water pressure
Effective stress
Example 2: An excavation was made in a clay stratum having 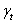 = 2 T/m3. When the depth was 7.5 m, the bottom of the excavation cracked and the pit was filled by a mixture of sand and water. The thickness of the clay layer was 10.5 m, and below it was a layer of pervious water-bearing sand. How much was the artesian pressure in the sand layer?
= 2 T/m3. When the depth was 7.5 m, the bottom of the excavation cracked and the pit was filled by a mixture of sand and water. The thickness of the clay layer was 10.5 m, and below it was a layer of pervious water-bearing sand. How much was the artesian pressure in the sand layer?
Solution:
When the depth of excavation was 7.5 m, at the interface of the CLAY and SAND layers, the effective stress was equal to zero.
Downward pressure due to weight of clay = Upward pressure due to artesian pressure
(10.5 - 7.5)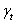 =
= 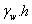 , where h = artesian pressure head
, where h = artesian pressure head
3 x 2 = 1 x h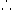 h = 6 m = 0.6 kg/cm2 or 6 T/m2 artesian pressure
h = 6 m = 0.6 kg/cm2 or 6 T/m2 artesian pressure
|
30 videos|126 docs|74 tests
|
FAQs on Importance of Effective Stress - Soil Mechanics - Civil Engineering (CE)
| 1. What is the importance of effective stress in civil engineering? |  |
| 2. How is effective stress different from total stress in civil engineering? |  |
| 3. What factors affect the effective stress in civil engineering? |  |
| 4. How is effective stress measured in civil engineering? |  |
| 5. What are the consequences of neglecting effective stress in civil engineering? |  |

















