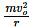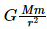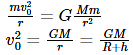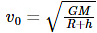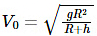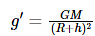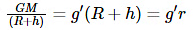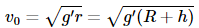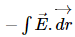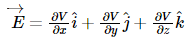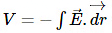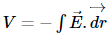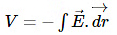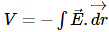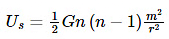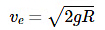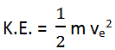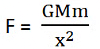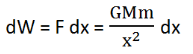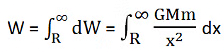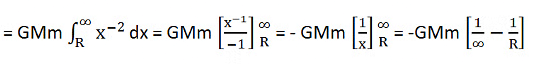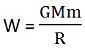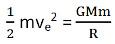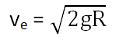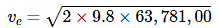Relation between Gravitational Field Intensity and Gravitational Potential
Integral Form:
V =
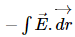
( If E is given and V has to be found using this formula)
Differential Form:
E = -dV/dr (If V is given and E has to be found using this formula)
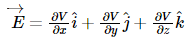
(components along x, y and z directions).
Gravitational Potential of a Point Mass
Consider a point mass M, the gravitational potential at a distance ‘r’ from it is given by;
V = – GM/r.
Gravitational Potential of a Spherical Shell
Consider a thin uniform spherical shell of the radius (R) and mass (M) situated in space. Now,
Case 1: If point ‘P’ lies inside the spherical shell (r<R): As E = 0, V is a constant.
The value of gravitational potential is given by, V = -GM/R.
Case 2: If point ‘P’ lies on the surface of the spherical shell (r=R):
On the surface of the earth, E = -GM/R2.
Using the relation
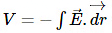
over a limit of (0 to R), we get,
Gravitational Potential (V) = -GM/R.
Case 3: If point ‘P’ lies outside the spherical shell (r>R):
Outside the spherical shell, E = -GM/r2.
Using the relation
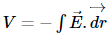
over a limit of (0 to r), we get,
V = -GM/r.
Gravitational Potential of a Uniform Solid Sphere
Consider a thin, uniform solid sphere of radius (R) and mass (M) situated in space. Now,
Case 1: If point ‘P’ lies inside the uniform solid sphere (r < R):
Inside the uniform solid sphere, E = -GMr/R3.
Using the relation
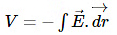
over a limit of (0 to r).
The value of gravitational potential is given by,
V = -GM [(3R2 – r2)/2R2]
Case 2: If point ‘P’ lies on the surface of the uniform solid sphere ( r = R ):
On the surface of a uniform solid sphere, E = -GM/R2. Using the relation
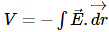
over a limit of (0 to R) we get,
V = -GM/R.
Case 3: If point ‘P’ lies outside the uniform solid sphere ( r> R):
Using the relation over a limit of (0 to r), we get, V = -GM/R.
Case 4: Gravitational potential at the centre of the solid sphere is given by V =(-3/2) × (GM/R).
Gravitational Self Energy
The gravitational self-energy of a body is defined as the work done by an external agent in assembling the body from the infinitesimal elements that are initially at an infinite distance apart.
Gravitational self energy of a system of ‘n’ particles:
Let us consider n particle system in which particles interact with each other at an average distance ‘r’ due to their mutual gravitational attraction; there are n(n – 1)/2 such interactions, and the potential energy of the system is equal to the sum of the potential energy of all pairs of particles, i.e.,
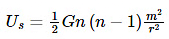
Solved Problems
Example 1. Calculate the gravitational potential energy of a body of mass 10 kg and is 25 m above the ground.
Solution:
Given, Mass m = 10 Kg and Height h = 25 m
G.P.E is given as,
U = m × g × h = 10 Kg 9.8 m/s2 × 25 m = 2450 J.
Example 2. If the mass of the earth is 5.98 ×1024 kg and the mass of the sun is 1.99 × 1030 kg, and the earth is 160 million km away from the sun, calculate the GPE of the earth.
Solution:
Given, the mass of the Earth (m) = 5.98 × 1024 Kg and mass of the Sun (M) = 1.99 × 1030 Kg
The gravitational potential energy is given by:
U = -GMm/r
U = (6.673 ∗ 10-11 ∗ 5.98 ∗ 1024 ∗1.99∗1030)/(160∗109) = 4963 x 1030 J
Example 3. A basketball weighing 2.2 kg falls off a building to the ground 50 m below. Calculate the gravitational potential energy of the ball when it arrives below.
Solution:
GPE = (2.2 kg)(9.8 m/s2)(50 m) = 1078 J.
Example 4: A 2 kg body free falls from rest from a height of 12 m. Determine the work done by the force of gravity and the change in gravitational potential energy. Consider the acceleration due to gravity to be 10 m/s2.
Solution:
Since, W = mgh
Substituting the values in the above equation, we get
W = 2 × 12 × 10 = 240 N
The change in gravitational potential energy is equal to the work done by gravity.
Therefore, Gravitational Potential Energy= 240 Joule.
Orbital Velocity Derivation
Orbital velocity is defined as the minimum velocity a body must maintain to stay in orbit.
Due to the inertia of the moving body, the body has a tendency to move on in a straight line. But, the gravitational force tends to pull it down. The orbital path, thus elliptical or circular in nature, represents a balance between gravity and inertia. Orbital velocity is the velocity needed to achieve a balance between gravity’s pull on the body and the inertia of the body’s motion. For a satellite revolving around the Earth, the orbital velocity of the satellite depends on its altitude above Earth. The nearer it is to the Earth, the faster the required orbital velocity.
A satellite runs into traces of Earth’s atmosphere, at lower altitudes, which creates drag. This drag causes decay the orbit, eventually making the satellite to fall back into the atmosphere and burn itself up.
Derivation of Orbital Velocity
To derive the orbital velocity, we concern ourselves with the following two concepts:
- Gravitational Force
- Centripetal Force
It is important to know the gravitational force because it is the force that allows orbiting to exist. A central body exerts a gravitational force on the orbiting body to keep it in its orbit. Centripetal force is also important, as this is the force responsible for circular motion.
For the derivation, let us consider a satellite of mass m revolving around the Earth in a circular orbit of radius r at a height h from the surface of the Earth. Suppose M and R are the mass and radius of the Earth respectively, then r = R + h.
To revolve the satellite, a centripetal force of
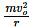 is needed which is provided by the gravitational force
is needed which is provided by the gravitational force
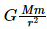 between the satellite and the Earth.
between the satellite and the Earth.
Therefore, equating both the equations, we get
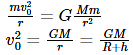 Simplifying the above equation further, we get
Simplifying the above equation further, we get
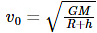 ……(eqn 1)
……(eqn 1)
But
GM = gR2
, where g is the acceleration due to gravity.
Therefore,
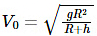 Simplifying the above equation, we get
Simplifying the above equation, we get
 Let g’ be the acceleration due to gravity in the ( at a height h from the surface)
Let g’ be the acceleration due to gravity in the ( at a height h from the surface)
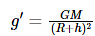 Simplifying further, we get
Simplifying further, we get
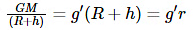 ……(eqn 2)
……(eqn 2)
Substituting (2) in (1), we get
Derivation of Escape Velocity
Derivation of escape velocity is a very common concept in the kinematics topic of physics, and often questions related to it are included in school exams. The escape velocity derivation is also important to understand the in-depth concepts better and thoroughly understand the related concepts.
With the help of the escape velocity formula, it is possible to calculate the minimum velocity that an object requires to overcome a particular planet’s or object’s gravitational pull. Here, the derivation of escape velocity is given in a very simple and easy-to-understand way that can help students learn this concept more effectively.Derivation of Escape Velocity:
Before checking the escape velocity derivation, it is important to know what escape velocity is and what are its related concepts. Check out the escape velocity of Earth for a detailed understanding of the minimum velocity required to overcome the earth’s gravitational pull.
Escape Velocity Formula:
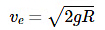
Derivation:
Assume a perfect sphere-shaped planet of radius R and mass M. Now, if a body of mass m is projected from a point A on the surface of the planet. An image is given below for better understanding:
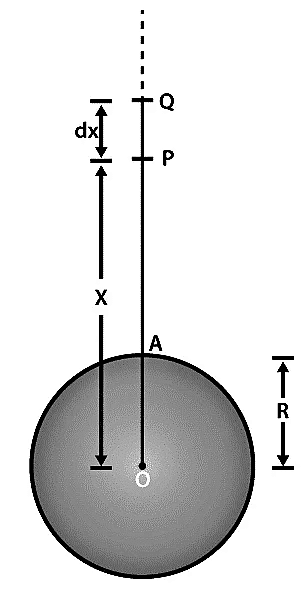
In the diagram, a line from the centre of the planet i.e. O is drawn till A (OA) and extended further away from the surface. In that extended line, two more points are taken as P and Q at a distance of x and dx, respectively from the centre O.
Now, let the minimum velocity required from the body to escape the planet b
ve
Thus, kinetic energy will be
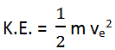
At point P, the body will be at a distance x from the planet’s centre and the force of gravity between the object and the planet will be
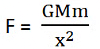
To take the body from P to Q i.e. against the gravitational attraction, the work done will be->
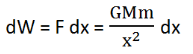
Now, the work done against the gravitational attraction to take the body from the planet’s surface to infinity can be easily calculated by integrating the equation for work done within the limits x = R to x = ∞.
Thus,
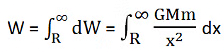
By integrating it further, the following is obtained:
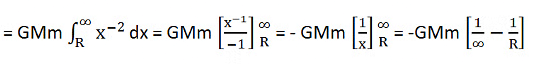
Thus, the work done will be:
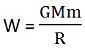
Now, to escape from the surface of the planet, the kinetic energy of the body has to be equal to the work done against gravity going from the surface to infinity. So,
K.E. = W
Putting the value for K.E. and Work, the following equation is obtained:
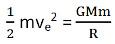
From this equation, the escape velocity can be easily formulated which is:

Putting the value of g = GM/R2, the value of escape velocity becomes:
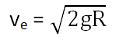
From these two equations, it can be said that the escape velocity depends on the planet’s radius and the planet’s mass only and not on the body’s mass.
Escape Velocity of Earth:
From the above equation, the escape velocity for any planet can be easily calculated if the mass and radius of that planet are given. For earth, the values of g and R are:
g = 9.8 ms-2
R = 63,781,00 m
So, the escape velocity will be:
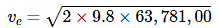
Escape Velocity of Earth= 11.2 km/s.