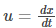Important Derivations: Mechanical Properties of Fluids | Physics Class 11 PDF Download
| Table of contents |

|
| Derivation of Stoke’s Law |

|
| Derivation Of Reynolds Number |

|
| Terminal Velocity Derivation |

|
| Derivation of Continuity Equation |

|
Derivation of Stoke’s Law
What is Stoke’s Law?
Stoke’s Law is a mathematical equation that expresses the settling velocities of the small spherical particles in a fluid medium. The law is derived considering the forces acting on a particular particle as it sinks through the liquid column under the influence of gravity. The force that retards a sphere moving through a viscous fluid is directly proportional to the velocity and the radius of the sphere, and the fluid’s viscosity.
Stoke’s Law Equation
Sir George G. Stokes, an English scientist, clearly expressed the viscous drag force F as: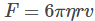
Where r is the sphere radius, η is the fluid viscosity, and v is the sphere’s velocity.
Stoke’s Law Derivation
From Stoke’s Law viscosity equation, we know that viscous force acting on a sphere is directly proportional to the following parameters:
- the radius of the sphere (r)
- coefficient of viscosity (η)
- the velocity of the object (v)
Mathematically, this is represented as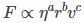
Now let us evaluate the values of a, b and c.
Substituting the proportionality sign with an equality sign, we get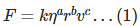
Here, k is the constant of proportionality, a numerical value with no dimensions.
Writing the dimensions of parameters on either side of equation (1), we get
[MLT–2] = [ML–1T–1]a [L]b [LT-1]c
Simplifying the above equation, we get
[MLT–2] = Ma ⋅ L–a+b+c ⋅ T–a–c… (2)
According to classical mechanics, mass, length and time are independent entities.
Equating the superscripts of mass, length and time, respectively from equation (2), we get
a = 1… (3)
–a + b + c = 1… (4)
–a –c = -2 or a + c = 2… (5)
Substituting (3) in (5), we get
1 + c = 2
c = 1 (6)
Substituting the value of (3) & (6) in (4), we get
–1 + b + 1 = 1
b = 1 (7)
Substituting the value of (3), (6) and (7) in (1), we get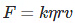
The value of k for a spherical body was experimentally obtained as
6π
Therefore, the equation gives the viscous force on a spherical body falling through a liquid.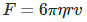
Terminal Velocity Formula
In the case of raindrops, initially, it is due to gravity that it accelerates. As the velocity increases, the retarding force also increases. Finally, when viscous force and the buoyant force is equal to the force due to gravity, the net force becomes zero, and so it does the acceleration. The raindrop then falls with a constant velocity, known as terminal velocity. Thus, in equilibrium, the terminal velocity vt is given by the equation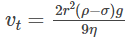
ρ and σ are sphere and fluid mass densities, respectively.
From the equation above, we can infer that the terminal velocity depends on the square of the radius of the sphere and is inversely proportional to the viscosity of the medium.
Stoke’s Law Example
Q: A solid metal ball is falling in a long liquid column and has attained a terminal velocity of 4 m/s. What is the viscosity of the liquid if the radius of the metal ball is r = 5 cm and its density is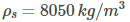
(The density of liquid is 1000 𝑘𝑔/𝑚3 and g is 10 m/s2.)
Ans:
The radius of the sphere is r = 0.05 m.
The density of the sphere is 𝜌s = 8050 kg/m3
The density of the liquid is 𝜌s= 1000 kg/m3
The terminal velocity is 4 m/s
Let the viscosity of the liquid be 𝜂.
Substituting the values in the terminal velocity equation, we get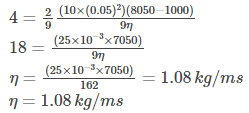
Stoke’s Law Applications
Stokes’s law finds application in several areas such as:
- Settling of sediment in freshwater
- Measurement of the viscosity of fluids
Derivation Of Reynolds Number
What is Reynolds Number?
Reynolds number referred to as Re is a dimensionless quantity which is used in fluid mechanics to predict the flow patterns in different fluid flow conditions. It is defined as the ratio of inertial force to viscous force within the fluid. The mathematical representation is given as: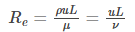
Where,
- ⍴ is the density of the fluid in kg.m-3
- 𝜇 is the dynamic viscosity of the fluid in N.s.m-2
- 𝜈 is the kinematic viscosity of the fluid in m2.s-1
- u is the velocity of a fluid with respect to the object in m.s-1
- L is the characteristic linear dimension in m
Using Reynolds number, it becomes easy to determine whether the fluid flow is laminar or turbulent. Following are the boundary values of a circular pipe that can be used to determine the flow pattern:
- If Re > 2300, then the flow is said to be laminar.
- If 2300 < Re < 4000, then the flow is said to be transient.
- If Re > 4000, then the flow is said to be turbulent.
Reynolds Number Derivation
The mathematical form of the Reynolds number can be derived as follows:
Re = inertial force/viscous force
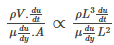

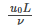
Where,
- t is the time
- y is the cross-sectional position
- is the flow speed

- τ is the shear stress in Pa
- A is the cross-sectional area of the flow
- V is the volume of the fluid element
- L is the characteristic linear dimension in m
- u0 is the maximum speed of the object relative to the fluid in m.s-1
- ⍴ is the density of the fluid in kg.m-3
- 𝜇 is the dynamic viscosity of the fluid in N.s.m-2
- 𝜈 is the kinematic viscosity of the fluid in m2.s-1
Following is the Reynolds number representation for the flow in a pipe: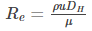
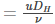
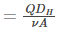
Where,
- DH is the hydraulic diameter of the pipe in m
- Q is the volumetric flow rate in m3.s-1
- A is the pipe’s cross-sectional area in m2
- u is the mean velocity of the fluid in m.s-1
- ⍴ is the density of the fluid in kg.m-3
- 𝜇 is the dynamic viscosity of the fluid in N.s.m-2
- 𝜈 is the kinematic viscosity of the fluid in m2.s-1
Critical Reynolds number and hydraulic diameter
Critical Reynold number of any fluid flow is defined when the flow pattern changes from laminar to turbulent. It is referred to as Recr. The critical Reynold number is not fixed as it varies from geometry to geometry and also is dependent on flow conditions.
For a circular pipe, the critical Reynolds number is given as Recr=2300 and for non-circular pipes it depends on the hydraulic diameter Dh which is defined as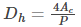
Where,
Ac is the cross-sectional area of the pipe
P is the wetted perimeter of the pipe
Hydraulic radius is defined as the cross-sectional area of the channel divided by the wetted perimeter and referred as RH.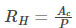
Following is the table of hydraulic diameter of non-circular tubes and channels:
Reynolds Number Examples
Example 1: A Newtonian fluid with a dynamic viscosity of 0.40 n.s.m-2 and a specific gravity of 0.93 flows through a 28 mm diameter pipe with a velocity of 2.9 m.s-1.
Ans: The density can be calculated using the specific gravity like
⍴=0.93(1000kg.m-3)
=930kg.m-3
The Reynolds number can be calculated using the formula as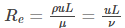
Re=(930kg.m-3) (2.9m.s-1) (28mm) (10-3m.mm-1)/(0.38Ns.m-2)
= 198 (kg.m.s-2)/N
Since Re=198 the flow is laminar.
Example 2: A person turns on the water tap in his kitchen. Water flows out from a copper pipe with 7.00 mm diameter at a velocity of 1.00 ms-1. The density of water in the pipe is 1000kg.m-3 and viscosity 0.00135 Pa.s-1. What is the Reynolds number, and what is the type of flow in the pipe?
Ans: The diameter of the pipe=7.00 mm = 0.007 m
Using Reynolds number formula: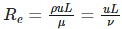
Re=(1000kg.m-3) (1.00m.s-1) (0.007m)/0.00135 Pa.s-1
=(1000kg.m-3) (1.00m.s-1) (0.007m)/0.00135 kg.m-1.s-1
=5185
Since Re=5185 the flow is turbulent.
Terminal Velocity Derivation
What is Terminal Velocity?
Terminal velocity is defined as the highest velocity attained by an object falling through a fluid. It is observed when the sum of drag force and buoyancy is equal to the downward gravity force acting on the object. The acceleration of the object is zero as the net force acting on the object is zero.
How to find Terminal Velocity?
In fluid mechanics, for an object to attain its terminal velocity, it should have a constant speed against the force exerted by the fluid through which it is moving.
The mathematical representation of terminal velocity is:
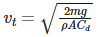
Where,
vt is the terminal velocity, m is the mass of the falling object, g is the acceleration due to gravity, Cd is the drag coefficient, 𝜌 density of the fluid through which the object is falling, and A is the area projected by the object.
Terminal Velocity Derivation
Deriving terminal velocity using mathematical terms according to the drag equation as follows:
F = bv2
Where b is the constant depending on the type of drag
(integrating the equations)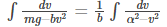
Where,
After integration,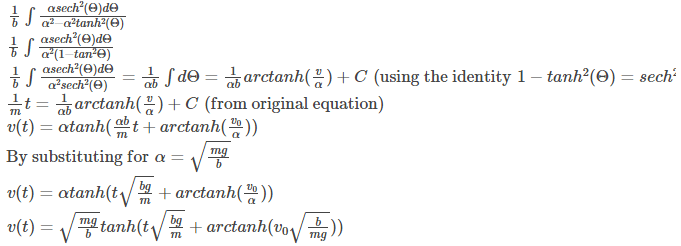
After substituting for vt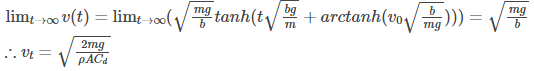
Therefore, above is the derivation of terminal velocity.
Derivation of Continuity Equation
According to the continuity equation, the product of the cross-sectional area of the pipe and the velocity of the fluid at any given point along the pipe is constant.
Continuity Equation Derivation
Continuity equation represents that the product of cross-sectional area of the pipe and the fluid speed at any point along the pipe is always constant. This product is equal to the volume flow per second or simply the flow rate. The continuity equation is given as:
R = A v = constant
Where,
- R is the volume flow rate
- A is the flow area
- v is the flow velocity
Assumption of Continuity Equation
Following are the assumptions of continuity equation:
- The tube is having a single entry and single exit
- The fluid flowing in the tube is non-viscous
- The flow is incompressible
- The fluid flow is steady
Derivation
Consider the following diagram:
Equation of Continuity
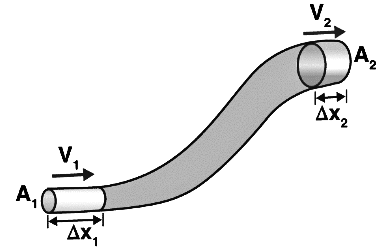
Now, consider the fluid flows for a short interval of time in the tube. So, assume that short interval of time as Δt. In this time, the fluid will cover a distance of Δx1 with a velocity v1 at the lower end of the pipe.
At this time, the distance covered by the fluid will be:
Δx1 = v1Δt
Now, at the lower end of the pipe, the volume of the fluid that will flow into the pipe will be:
V = A1 Δx1 = A1 v1 Δt
It is known that mass (m) = Density (ρ) × Volume (V). So, the mass of the fluid in Δx1 region will be:
Δm1= Density × Volume
⇒ Δm1 = ρ1A1v1Δt ——–(Equation 1)
Now, the mass flux has to be calculated at the lower end. Mass flux is simply defined as the mass of the fluid per unit time passing through any cross-sectional area. For the lower end with cross-sectional area A1, mass flux will be:
Δm1/Δt = ρ1A1v1 ——–(Equation 2)
Similarly, the mass flux at the upper end will be:
Δm2/Δt = ρ2A2v2 ——–(Equation 3)
Here, v2 is the velocity of the fluid through the upper end of the pipe i.e. through Δx2 , in Δt time and A2, is the cross-sectional area of the upper end.
In this, the density of the fluid between the lower end of the pipe and the upper end of the pipe remains the same with time as the flow is steady. So, the mass flux at the lower end of the pipe is equal to the mass flux at the upper end of the pipe i.e. Equation 2 = Equation 3.
Thus,
ρ1A1v1 = ρ2A2v2 ——–(Equation 4)
This can be written in a more general form as:
ρ A v = constant
The equation proves the law of conservation of mass in fluid dynamics. Also, if the fluid is incompressible, the density will remain constant for steady flow. So, ρ1 =ρ2.
Thus, Equation 4 can be now written as:
A1 v1 = A2 v2
This equation can be written in general form as:
A v = constant
Now, if R is the volume flow rate, the above equation can be expressed as:
R = A v = constant
This was the derivation of continuity equation.
Continuity Equation in Cylindrical Coordinates
Following is the continuity equation in cylindrical coordinates: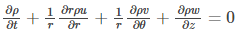
Incompressible Flow Continuity Equation
Following is the continuity equation for incompressible flow as the density, ρ = constant and is independent of space and time, we get:
∇.v = 0
Steady Flow Continuity Equation
Following is the continuity equation in cylindrical coordinates: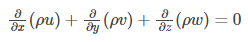
|
101 videos|325 docs|100 tests
|