Important Derivations: Mechanical Properties of Solids | Physics Class 11 PDF Download

Torsion Equation Derivation

Torsion equation or torsion constant is defined as the geometrical property of a bar’s cross-section that is involved in the axis of the bar that has a relationship between the angle of twist and applied torque whose SI unit is m4. The torsion equation is given as follows: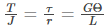

Torsion equation derivation

Following are the assumptions made for the derivation of torsion equation:

• The material is homogeneous (elastic property throughout)
• The material should follow Hooke’s law
• The material should have shear stress proportional to shear strain
• The cross-sectional area should be plane
• The circular section should be circular
• Every diameter of the material should rotate through the same angle
• The stress of the material should not exceed the elastic limit

Consider a solid circular shaft with radius R that is subjected to a torque T at one end and the other end under the same torque.
Angle in radius =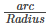

Arc AB = RӨ = Lγ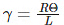

Where,
A and B: two fixed points on the circular shaft
γ: angle subtended by AB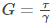

(Modulus of rigidity)
Where,
𝞃: shear stress
γ: shear strain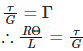

Consider a small strip of radius with thickness dr that is subjected to shear stress.

Where,
r: radius of small strip
dr: thickness of the strip
γ: shear stress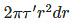

(torque at the center of the shaft)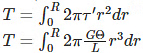

(substituting for 𝛕’ )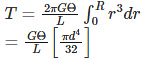

(after integrating and substituting for R )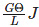

(substituting for the polar moment of inertia)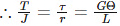

Bending Equation Derivation

Bending theory is also known as flexure theory is defined as the axial deformation of the beam due to external load that is applied perpendicularly to a longitudinal axis which finds application in applied mechanics.
For a material, flexural strength is defined as the stress that is obtained from the yield just before the flexure test. It represents the highest stress that is experienced within the material at the moment of its yield. 𝜎 is used as the symbolic representation of flexural strength.

Bending Equation derivation

Following are the assumptions made before the derivation of the bending equation:

• The beam used is straight with a constant cross-section.
• The beam used is of homogeneous material with a symmetrical longitudinal plane.
• The plane of symmetry has all the resultant of applied loads.
• The primary cause of failure is buckling.
• E remains the same for tension and compression.
• Cross-section remains the same before and after bending.

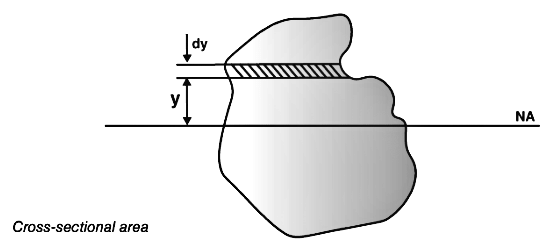
Consider an unstressed beam, which is subjected to a constant bending moment such that the beam bends up to radius R. The top fibres are subjected to tension whereas the bottom fibres are subjected to compression. The locus of points with zero stress is known as the neutral axis.
Bending Theory

With the help of the above figure, the following are the steps involved in the derivation of the bending equation:
Strain in fibre AB is the ratio of change in length to original length.
Strain in fibre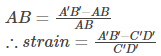

(as AB = CD and CD = C’D’)
CD and C’D’ are on the neutral axis and stress is assumed to be zero, therefore strain is also zero on the neutral axis.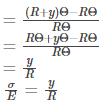

where E is Young’s Modulus of Elasticity
Or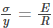

(eq.1)

(force acting on the strip with area dA)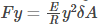

(momentum about neutral axis)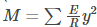

(total momentum for entire cross-sectional area)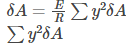

is known as the second momentum of the area and is represented as I.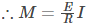

(eq.2)
From eq.1 and eq.2 we get,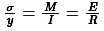

Therefore, the above is the bending theory equation.

Bulk Modulus Formula Derivation

Bulk Modulus

Bulk modulus of a substance is defined as the ratio of infinitesimal pressure increase to a decrease of the volume. Bulk modulus is meaningful only for a fluid. It is denoted as either K or B. The reciprocal of bulk modulus is compressibility of a substance and this is the relation between bulk modulus and compressibility.
The mathematical representation of bulk modulus is given as follows:
For bulk modulus K > 0;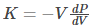

Where,
P: pressure
V: volume

Bulk Modulus For Unit Mass

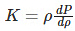
Where,
⍴: density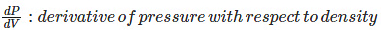

Bulk modulus in thermodynamics with constant temperature and constant entropy is given as follows:
Isentropic bulk modulus Ks;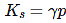

Isothermal bulk modulus K_T;

Where,
p: pressure
γ: heat capacity ratio
Following is the table of bulk modulus of a few common materials:

Bulk Modulus Formula Derivation

As we know the ratio between change in pressure to change in volumetric strain is dependent on bulk modulus of the material, following is the derivation showing the relationship: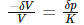

(negative sign to indicate that with increase in pressure, volume decreases)
Where,
δV: change in volume
δp: change in pressure
V: actual volume
K: bulk modulus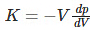

(as δp tends to 0) (eq.1)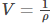

(unit mass of the substance) (eq.2)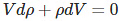

(after differentiation)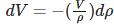

(eq.3)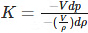

(after substituting eq.3 in eq.1)

Thus, above is the derivation of bulk modulus which is mainly applicable to liquids as gases are highly compressible which makes K vary.

Solved Example

Q1: What is the bulk modulus of a body that experienced a change of pressure of 5 x 10⁴ N/m² and its volume goes from 4 cm³ to 3.9 cm³?
Ans: The bulk modulus is calculated using the formula,
B = ΔP /(ΔV/V)
B = (5 x 10⁴ N/m²)/((4 cm³ – 3.9 cm³)/4 cm³) = 0.125 x 10⁴ N/m²
B = 1.25 x 10⁴ N/m²

Q2: In the ammunition testing centre the pressure is found to be 255 MPa. Calculate the change in volume of the copper piece when subjected to this pressure in percentage. The bulk modulus of copper is 1.38 x 10¹¹ Pa.
Ans: The pressure in the testing centre is 255 MPa.
Bulk modulus, K = V(∆P) / ∆V
Substituting the values,
(ΔV / V) = 255 × 10⁶ / 1.38 × 10¹¹ × 100
Therefore, the change in volume percentage is 0.184 %