Important Derivations: Thermodynamics | Physics Class 11 PDF Download
Work Done in Adiabatic Process Derivation
An adiabatic process is a thermodynamic process during which no heat energy is transferred across the boundaries of the system. This does not mean the temperature is constant, but rather that no heat is transferred into or out of the system. In this article let us learn about the adiabatic process, examples, adiabatic process equation derivation and the adiabatic index.
Adiabatic Process Examples
- The vertical flow of air in the atmosphere
- When the interstellar gas cloud expands or contracts.
- The turbine is an example of the adiabatic process as it uses heat as a source to produce work.
Adiabatic Process Derivation
The equation for an adiabatic process can be derived from the first law of thermodynamics relating to the change in internal energy dU to the work W done by the system and the heat dQ added to it.
dU=dQ-dW
dQ=0 by definition,
Therefore, 0=dQ=dU+dW
The work done dW for the change in volume V by dV is given as PdV.
The first term is related to specific heat which is defined as the heat added per unit temperature change per mole of a substance. The heat that is added increases the internal energy U such that it justifies the definition of specific heat at constant volume given as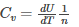
Where,
n: number of moles
Therefore,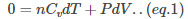
From the ideal gas law, we have
nRT=PV (eq.2)
Therefore, nRdT=PdV+VdP (eq.3)
By combining equation 1 and equation 2, we get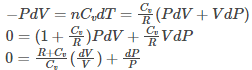
When the heat is added at constant pressure Cp, we have
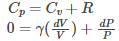
Where the specific heat ɣ is given as: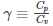
From calculus, we have,

Hence, the equation is true for an adiabatic process in an ideal gas.
Adiabatic Index
The adiabatic index is also known as the heat capacity ratio and is defined as the ratio of heat capacity at constant pressure Cp to heat capacity at constant volume Cv. It is also known as the isentropic expansion factor and is denoted by ɣ.
Where,
C: heat capacity
c: specific heat capacity
The adiabatic index finds application reversible thermodynamic process involving ideal gases and speed of sound is also dependent on the adiabatic index.
Derivation of Phase Rule
The phase rule describes the possible number of degrees of freedom in an enclosed system at equilibrium, in terms of the number of separate phases and the number of chemical constituents in the system. It was deduced by J.W Gibbs in the 1870s. Today, the phase rule is popularly known as the Gibbs phase rule all over the world. Here, in the article, we will be discussing the derivation of the phase rule.
Gibbs Phase Rule
Gibbs phase rule states that if the equilibrium in a heterogeneous system is not affected by gravity or by electrical and magnetic forces, the number of degrees of freedom is given by the equation
F=C-P+2
where, C is the number of chemical components,
P is the number of phases.
Basically, it describes the mathematical relationship for determining the stability of phases present in the material at equilibrium conditions.
In the next section, let us look at the phase rule derivation.
Phase Rule Derivation
Gibbs phase rule on the basis of the thermodynamic rule can be derived as follows:
First, let us consider a heterogeneous system consisting of Pn number of phases and Cn number of components in equilibrium. Let us assume that the passage of a component from one phase to another doesn’t involve any chemical reaction. When the system is in equilibrium, it can be described by the following parameters:
- Temperature
- Pressure
- The composition of each phase
a. The total number of variables required to specify the state of the system is:
- Pressure: same for all phases
- Temperature: same for all phases
- Concentration
The independent concentration variable for one phase with respect to the C components is C – 1. Therefore, the independent concentration variables for P phases with respect to C components is P (C – 1).
Total number of variables = P (C – 1) + 2….. (1)
b. The total number of equilibria:
The various phases present in the system can only remain in equilibrium when the chemical potential (µ) of each of the component is the same in all phases, i.e.
The number of equilibria for each P phases for each component is P – 1.
For C components, the number of equilibria for P phases is C ( P – 1).
Hence, the total number of equilibria involved is E = C (P – 1)… (2)
Equating eq (1) and (2), we get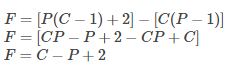
Derivation Of Heat Equation
Derivation of the heat equation can be explained in one dimension by considering an infinitesimal rod. The heat equation is a parabolic partial differential equation, describing the distribution of heat in a given space over time. The mathematical form is given as: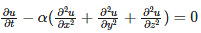
Heat equation derivation in 1D
Assumptions:
- The amount of heat energy required to raise the temperature of a body by dT degrees is sm.dT and it is known as the specific heat of the body where,
s: positive physical constant determined by the body
m: a mass of the body
- The rate at which heat energy crosses a surface is proportional to the surface area and the temperature gradient at the surface and this constant of proportionality is known as thermal conductivity which is denoted by 𝛋
Consider an infinitesimal rod with cross-sectional area A and mass density ⍴.
Temperature gradient is given as: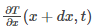
Rate at which the heat energy crosses the right hand is given as: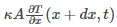
Rate at which the heat energy crosses in the left hand is given as: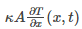
For the temperature gradients to be positive on both sides, temperature must increase.
As the heat flows from the hot region to a cold region, heat energy should enter from the right end of the rod to the left end of the rod.
Therefore,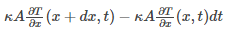
Where, dt: infinitesimal time interval
Temperature change in the rod is given as: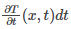
Mass of the rod is given as: ⍴Adx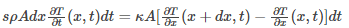
Dividing both sides by dx and dt and taking limits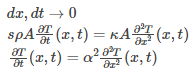
Where,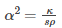
is the thermal diffusivity.
Hence, the above is the heat equation.
|
101 videos|325 docs|100 tests
|

|
Explore Courses for Class 11 exam
|

|
















