Important Derivations: Work, Energy, and Power | Physics for ACT PDF Download
| Table of contents |

|
| Derivations of Work, Energy, and Power |

|
| Derivation of Potential Energy |

|
| Derivation of Work Energy Theorem |

|
| Derivation of Kinetic Energy |

|
Derivations of Work, Energy, and Power
Work-Energy Theorem
Kf - Ki = W
where Ki amd Kf are initial and final kinetic energy of the body. W is the workdone on the body.
Conservation of Mechanical Energy
if ΔK is change in kinetic energy and ΔV is change in potential energy, then ΔK + ΔV = Δ(K+V) = 0
i.e., sum of kinetic energy and potential energy, (K+V) is constant
that leads the conservation of energy relation, Kf + Vf = Ki + Vi
In the above relation K stands for kinetic energy and V is for potential energy.
Subscript i refers initial state and f refers final state.
Potential energy V stored in spring , V = (1/2) k x2
where k is spring constant defined as F = kx ,
i.e. spring is elongated or compressed by a length x due to the application of force F.
Instantaneous power = Force × instantaneous velocity = F × v
Inelastic collision : Momentum is conserved but energy is not conserved
Loss of kinetic energy in Inelastic collision ,
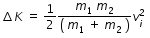
m1 and m2 are respective mass of colliding particles. vi is initial velocity of one particle before collision while another particle is at rest before collision.
elastic collision : Both momentum and energy are conserved
Let m1 is mass of a particle moving with initial speed v1i is colliding with another particle of mass m2
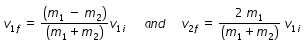
if both masses are equal, particle of mass m1 will come rest after collision and other particle of mass m2
Special case (2) : if m2 > m1 , particle of mass m1 will move in opposite direction after collision.
Derivation of Potential Energy
The derivation of potential energy is provided here. Potential energy is defined as the energy that is held by an object because of its position with respect to other objects. The SI unit of potential energy is joule whose symbol is J. Potential energy term was introduced by Scottish engineer and physicist William Rankine in the 19th century.
The gravitational potential energy of an object, elastic potential energy of an extended spring, and electric potential energy of an electric charge are the most common type of potential energies observed.
Potential Energy Derivation
Potential energy is the work done to take a body to a certain height. For a body with mass m, h is the distance to which it is raised and g is the gravitational force acting on the body, then work done W is given as:
W = force * displacement
W = mg * h
∴ W = mgh
As the work done is equal to mgh which is gained by the object, potential energy Ep is given as:
Ep = mgh
Therefore, the above is the derivation of potential energy.
Derivation of Work Energy Theorem
The derivation of the work-energy theorem is provided here. The work-energy theorem, also known as the principle of work and kinetic energy, states that the total work done by the sum of all the forces acting on a particle is equal to the change in the kinetic energy of that particle. This explanation can be extended to rigid bodies by describing the work of rotational kinetic energy and torque.
What Is Kinetic Energy?
Kinetic energy is the energy possessed by an object due to its motion or movement. In simple words, it is the energy of motion, observable as the movement of an object, particle, or set of particles.
Work-Energy Theorem Derivation
The work ‘W’ done by the net force on a particle is equal to the change in the particle’s kinetic energy (KE).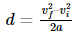
Check the detailed work-energy theorem derivation given below.
Let us consider a case where the resultant force ‘F’ is constant in both direction and magnitude and is parallel to the velocity of the particle. The particle is moving with constant acceleration along a straight line. The relationship between the acceleration and the net force is given by the equation “F = ma” (Newton’s second law of motion), and the particle’s displacement ‘d’, can be determined from the equation: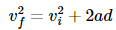
Obtaining,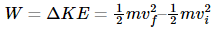
The work of the net force is calculated as the product of its magnitude (F=ma) and the particle’s displacement. Substituting the above equations yields: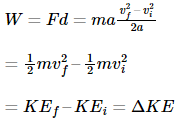
Derivation of Kinetic Energy
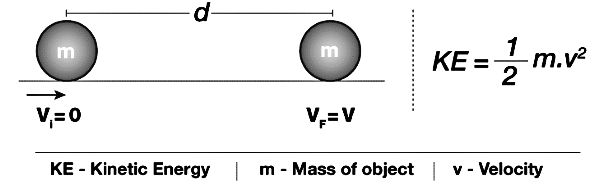
The kinetic energy of a body is the energy that is possessed due to its motion. Kinetic energy is the work needed to accelerate an object of a given mass from rest to its stated velocity. The derivation of kinetic energy is one of the most common questions asked in the examination. To excel in their examinations, students must properly understand the kinetic energy derivation method.
Kinetic energy depends upon the body’s velocity and mass. If the body’s velocity is zero, then the kinetic energy will also be zero. The derivation of kinetic energy is given below so that students can understand the concept more effectively. The kinetic energy formula derivation can be done using algebra and calculus. Both methods are explained below.
Derivation of Kinetic Energy using Algebra
The kinetic energy derivation using only algebra is one of the best ways to understand the formula in-depth.
Starting with the work-energy theorem and then adding Newton’s second law of motion, we can say that,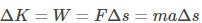
Now, taking the kinematics equation and rearranging it, we get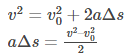
Combining the 2 expressions, we get,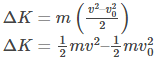
Now we already know that kinetic energy is the energy that it possessed due to its motion. So the kinetic energy at rest should be zero. Therefore, we can say that kinetic energy is:
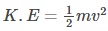
Derivation of Kinetic Energy using Calculus
The derivation of kinetic energy using calculus is given below. To derive an expression for kinetic energy using calculus, we will not need to assume anything about the acceleration.
Starting with the work-energy theorem and Newton’s second law of motion we can say that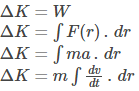
Now rearranging the differential terms to get the function and the integral into an agreement.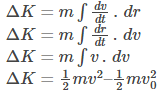
Now, we know that the kinetic energy of a body at rest is zero. So we can say that the kinetic energy is: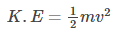
|
169 videos|149 docs|75 tests
|
FAQs on Important Derivations: Work, Energy, and Power - Physics for ACT
| 1. What is the derivation of potential energy? |  |
| 2. How is the work-energy theorem derived? |  |
| 3. What are some important derivations related to work, energy, and power? |  |
| 4. How is potential energy related to work and energy? |  |
| 5. What is the significance of understanding the derivations of work, energy, and power? |  |














