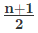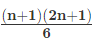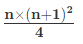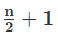Important Formula: Averages | Quantitative Ability for SSC CHSL PDF Download
Basic Averages Formulas
Mathematically, it is defined as the ratio of summation of all the numbers to the number of units present in the list.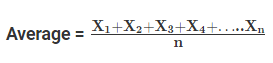
OR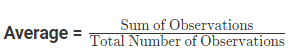

Average Speed and Velocity Formula
Average speed is the total distance covered by a body within a specific time interval. The calculation of average speed involves the use of the formula provided below.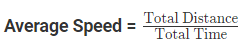
Case 1: When one travels at speed ‘a’ for half the time and speed ‘b’ for other half of the time. Then, average speed is the arithmetic mean of the two speeds.
Average Speed= 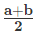
Case 2: When one travels at speed ‘a’ for half of the distance and speed ‘b’ for other half of the distance.Then, average speed is the harmonic mean of the two speeds.
Average Speed= 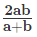
Case 3: When one travels at speed a for one-third of the distance, at speed b for another one-third of the distance and speed c for rest of the one-third of the distance
or:
Average Speed = 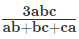
Average Velocity: It can be defined as total displacement divided by total time. We calculate Average Velocity using the below formula
Average Velocity =
Formula of Averages Related to Numbers:
- Average of ‘n’ consecutive Natural Numbers =

- Average of the square of consecutive n natural numbers =

- Average of cubes of consecutive n natural numbers =

- Average of n consecutive even numbers = (n+1)
- Average of consecutive even numbers till n =

- Sum of 1st n even consecutive natural numbers is = n(n + 1)
- Sum of 1st n odd consecutive natural numbers is = n2
Q1: The average of 10 numbers is 23. If each number is increased by 4, what will the new average be?
Sol:
Average of 10 numbers = 23
Sum/Total numbers = 23
Sum/10 = 23
Sum of the 10 numbers = 230
If each number is increased by 4, the total increase = 4 x 10 = 40
New sum = 230 + 40 = 270
Therefore, the new average = 270/10 = 27
Q2: The mean of 25 numbers is 36. If the mean of the first 13 numbers is 32 and that of the last 13 numbers is 39, find the 13th number.
Sol:
Mean of the first 13 numbers = 32
Sum of the first 13 numbers = (32 × 13) = 416
Mean of the last 13 numbers = 39
Sum of the last 13 numbers = (39 × 13) = 507
Mean of 25 numbers = 36
Sum of all the 25 numbers = (36 × 25) = 900
The 13th number is included in both the first 13 numbers and the last 13 numbers. Therefore, we have counted it twice in the total of 416+507
Therefore, the 13th number= (416 + 507 – 900) = 23
Hence, the 13th number is 23
Q3: A batsman makes a score of 87 runs in the 17th inning and thus increases his average by 3. Find his average after 17th inning?
Sol:
Let the average after 17th inning = x
Then average after 16th inning = x – 3
16(x-3)+87 = 17x
x = 87 – 48 = 39
Q4: The average weight of a group of seven boys is 56 kg. The individual weights (in kg) of six of them are 52, 57, 55, 60, 59 and 55. Find the weight of the seventh boy.
Sol:
Average weight of 7 boys = 56 kg.
Total weight of 7 boys = (56 × 7) kg = 392 kg.
Total weight of 6 boys = (52 + 57 + 55 + 60 + 59 + 55) kg
= 338 kg.
Weight of the 7th boy = (total weight of 7 boys) – (total weight of 6 boys)
= (392 – 338) kg
= 54 kg.
Therefore, the weight of the seventh boy is 54 kg.
Q5: The average of 7 consecutive numbers is 20. What is the largest of these numbers?
Sol:
Let the 7 consecutive numbers be x, x + 1, x + 2, x + 3, x + 4, x + 5 and x + 6,
As per the given condition;
[x + (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) + (x + 6)] / 7 = 20
⇒ 7x + 21 = 140
⇒ 7x = 119
⇒ x =17
The largest of the 7 consecutive numbers is the last one, x + 6
x + 6 = 17+6 = 23
Q6 : In a school, there are five friends- A, B, C, D and E. The weight of A is equal to the average weight of B, C and D and the weight of B is equal to the average weight of A, C and D. The average weight of A and C is equal to the average weight of C and D. E is 30 kg heavier than C and the average weight of B and D is 60 kg. What is the average weight (in kgs) of A, B, C, D and E?
Let the weight of four friends A, B, C, D and E are a, b, c, d and e kgs respectively
From the question,
3a = b + c + d ----------- (i)
3b = a + c + d ----------(ii)
Subtracting equation (i) and (ii)
3a – 3b = b – a
b = a ---- (iii)
Adding equation (i) and (ii)
3a + 3b = a + b + 2c + 2d
a + b = c + d ---- (iv)
The average weight of A and C is equal to the average weight of C and D
It means, a + c = c + d
a = d
Put a = d in equation (iv)
We get b = c
It means, b = a = c = d
The average weight of B and D is 60 kgs
b + d = 60 × 2 = 120 kgs
So, b = d = 60 kgs = a = c
E is 30 kg heavier than C
e = (60 + 30) kgs
By solving, e = 90 kg
The sum of the weight of A, B, C, D and E = 60 + 60 + 60 + 60 + 90 = 330 kgs
The average = 330 /5= 66 kgs
Q7 : The average of a group of 15 members initially increases from 60kg to 65 kg when A, B and C join the group. The weight of A, B and C are in the ratio 3 : 4 : 2. What is the difference between weight of A and C?
The average weight increases by 5 kg
So total increase in weight = 3 × 60 + 18 × 5 = 270 kg
A : B : C = 3 : 4 : 2
So weight of A = 90, B = 120 and C = 60 kg
Required difference = 90 – 60 = 30 kg
Q8 :The average score (runs/match) of Dravid before the start of World Cup was 35. In the world cup of 6 matches, his total score was 355 runs. Find the total number of matches played by him till date, if his new average after the series is 37.5.
Let the total number of matches Dravid has played, till the start of world cup be X So, total runs scored by Dravid till the beginning of the world cup be 35 × X
After the world cup, the new average will be
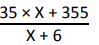
According to question,
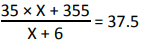
37.5 × X + 225 = 35 × X + 355
2.5 × x = 130
⇒X = 52
Hence, the total number of matches played by Dravid till date = X + 6 = 52 + 6 = 58
Q9 : S1, S2 and S3 are three arithmetic progression series. S1 is an increasing series with elements A, B, C, D and E. S2 is a decreasing series with elements P, Q, R , S and T. S3 is formed on adding the corresponding elements of S1 and S2 i.e. first element of S3 is sum of first element of S1 and S2, similarly second and so on. In S3, the average of all the terms is 30 and the last term is 12 more than the first term. What is the sum of second term and last term of S3?
Let S3 = D, D + z, D + 2z, D + 3z, D + 4z
Difference between last and first = 12
4z = 12
z = 3
Average of all terms = 30
D + 2z = 30
D = 24
Second + Last = 2D + 5z = 48 + 15 = 63
Q10: Rajiv decided to go for a dinner with his 12 friends. He paid Rs. 145 and each of his friends paid some equal amount. They later found out that the average amount that should be paid by all of them was 5 more than what was actually paid by each of his friends. How much money did each of his friend pay?
Let the amount paid by each of Rajiv’s friend be Rs x
Total amount paid by them in all = Rs. (145 + 12x)
Average amount that should have been paid by Rajiv’s friends = 5 + x

x=80
|
37 videos|24 docs|66 tests
|
FAQs on Important Formula: Averages - Quantitative Ability for SSC CHSL
| 1. What is the formula to calculate the average of a set of numbers? |  |
| 2. How do you find the average if the numbers are in a data set? |  |
| 3. Can you explain the difference between mean, median, and mode in averages? |  |
| 4. How does one calculate the weighted average? |  |
| 5. What are some real-life applications of averages? |  |

|
Explore Courses for SSC CHSL exam
|

|