Important Formulas for CAT Percentages
What are Percentages?
- The percent is derived from the Latin word ‘Centum’ which means for ‘every 100’ or ‘per hundredth.’
- Percentage is the representation of a number, ratio, fraction, or decimal as a fraction of 100.
- If we need to calculate a percentage of a number, we should divide it by its entirety and then multiply it by 100. The proportion therefore refers to a component per hundred.

How to Calculate a Percentage
1. Number: To represent a number ‘N’ into a percentage, just simply multiply the number with 100.
Example: Convert ‘4’ into a percentage.
Sol: Representation of 4 in Percentage will be
= 4 × 100 = 400%
2. Fraction: To represent a fraction into a percentage, just simply multiply the fraction with 100 and to convert the percentage into fraction just simply divide the percentage by 100.
Percentage = (Part / Whole) × 100
Example: Convert the fraction 3/5 into percentage.
Sol: Representation of 3/5 into Percentage will be
3/5 x 100 = 60%
3. Ratio: To convert the ratio into percentage, first convert the ratio into a fraction and then multiply the fraction with 100.
Example: Convert the ratio 2 : 5 into percentage.
Sol: Converting ratio into fraction we get
Now, the representation of 2/5 into percentage will be
4. Decimal: To represent a decimal into percentage, just simply multiply the decimal by 100 and to convert the percentage into a decimal just simply divide the percentage by 100.
Example: Convert 0.773 into percentage
Sol: Representation of 0.773 into percentage will be
=0.773 × 100=77.3%
Concept of Percentage Change
Whenever the value of measured quantity changes, the change can be captured through the following methods:a. Absolute Value Change
It refers to the actual change in the measured quantity. For instance, if sales in year one is ₹5000 crore and the sales in year two is ₹6000 crore, then the absolute value of the change is ₹1000 croreb. Percentage Change
It is the percentage change obtained by the formulaPercentage change = (Absolute value change/ Original quantity) x 100
= 1000/5000 * 100 = 20%
Important Formulas
- Percentage Change of A from B = (A-B)/B x 100
- Percentage Change from A to B = (B-A)/A x 100
- How much more is A relative to B = (A-B)/B x 100
Example : The population of a city grew from 20 lac to 22 lac. Find the
(a) percentage change
(b) percentage change based on the final value of population
Sol: (a) percentage change = (Absolute Change/ Original Quantity) x 100
= (2/20) × 100 = 10%
(b) percentage change on the final value = (Absolute Change/ Original Quantity) x 100
= (2/22) x 100 = 9.09%
Difference b/w Percentage Point Change and Percentage Change
- Percentage Point Change is simply the difference between the given percentages.
- But, as we have already seen that Percentage Change = (Absolute Change/ Original Quantity) x 100
- Example: The savings rate as a percentage of the GDP was 25% in the first year and 30% in the second year. Assume that there is no change in the GDP between the two years. Calculate the Percentage point change and the percentage change?
- Sol: Percentage Point change in savings rate = 30%-25%
= 5 percentage points.
Percentage Change in Savings = (5/25)x 100
= 20%
Increase/Decrease in Percentage
Percentage Increase
When comparing the increase in a quantity over a period of time, we first find the difference between the original value and the increased value. We then use this difference to find the relative increase against the original value and express it in terms of percentage. The formula for percentage increase is given by:
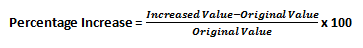
and
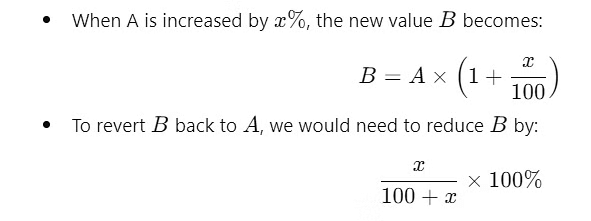
Percentage Decrease
When comparing the decrease in a quantity over a period of time, we first find the difference between the original value and the decreased value. We then use this difference to find the relative decrease against the original value and express it in the form of a percentage. The formula for percentage decrease is given by:
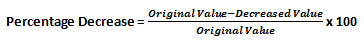
and
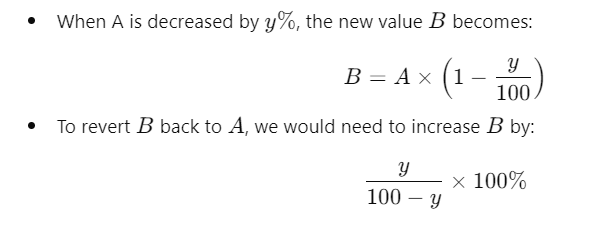
Solved Examples
Example 1: Raghu has 20% more toffees than Pinki. How much percent less toffees Pinki has as compared to Raghu?
Sol:Here, the quantity of toffees with Raghu is 20% more than Pinki, i.e., the value of x is 20.
So, the percentage of toffees with Pinki as compared to Raghu will be less by:
Note: When ‘percentage increased/decreased by X%’ is given for a quantity, then the actual increase/decrease in the quantity is (100± X%).
While, when ‘percentage increase/decrease to X%’ is given for a quantity, then the actual increase/decrease in the quantity is (±X%)
For example, if the salary of a person is decreased by 20%, then the final salary of the person will be 80% of the original salary while if the salary of a person is decreased to 20% of the final salary of the person will be 20% of the original salary.
Example 2: A TV cost $100 last year but now costs $125. Find the price increase.
Sol: To determine the price increase, subtract the old price from the new price: 125 - 100 = 25.
Next, divide this by the old price: 25 divided by 100 = 0.25. Multiply that number by 100: 0.25 × 100 = 25, or 25%. So, the TV price has increased 25% over the past year.125 - 100 = 25
25 / 100 = .025
.025 × 100 = 25%
Example 3: The annual salary of Suresh increased from Rs 18,00,000 to Rs 22,00,000. Find the percentage increase.
Sol: Original salary = Rs 18,00,000
Increased salary = Rs 22,00,000
Increase in salary = Rs 22,00,000 – Rs 18,00,000 = Rs 4,00,000
Thus, percentage increase in salary = (increase in salary/original salary) x 100
= (4,00,000/18,00,000) x 100 = 22.22%
Example 4: A TV cost $100 last year but now costs only $75.Determine the price decrease.
Sol: To determine the price decrease, subtract the new price from the old price: 100 - 75 = 25. Divide his number by the old price: 25 divided by 100 = 0.25. Multiply that number by 100: 0.25 × 100 = 25. or 25%. The TV costs 25% less than it did the year before.
100 - 75 = 25
25 / 100 = 0.25
.25 × 100 = 25%
Concept of Product Constancy
- Product constancy means the consistency of the product even though there is an increase or decrease in its price.
You can also call product constancy as inverse proportionality. - In product constancy, you have to reduce the consumption when there is an increase in price so that your budget remains the same.
- Product constancy involves the problems with two dependent quantities whose product is the third quantity. Thus, if there is an increase in the first quantity, then to make the third quantity constant, we have to increase/decrease the second quantity.
- Some relations from which questions on product constancy are asked are:
- Expenditure = Price * Consumption
- Price = Rate * Quantity
- Distance = Speed * Time
- Work done = Time taken * Efficiency
- Area of Rectangle = Length * Breadth
Solved Examples
Example 1: The price of sugar is increased by 25%. If a family does not want to increase/decrease their expenditure, then by what percent should it decrease their consumption?
Sol: We know, Expenditure = Price * Consumption
As, price is increased by 25%
So, here x = 25%
Thus, to remain the expenditure constant we should decrease the consumption by
Example 2: Normally A does a certain work. But A is absent so Ravi has two options: B or C. B can finish the work by taking 6 hrs more than A while C is 1.5 times more efficient than B and can finish the work 4 hrs earlier. Find the usual time taken by A.
Sol: Case 1: B efficiency = x ,6 hrs more than A
Case 2: C efficiency = 1.5x 4 hrs less than ANow we know efficiency and time are two inversely proportional quantities. Taking case 1 as original, efficiency increases by ½ so the time is taken will decrease by 1/3 from case1 to case 2. 6 hrs more than A and 4 hrs less than A means a difference of 10 hrs. As we have already calculated, the time taken will decrease by 1/3 and the difference is 10 hrs this means the original time taken in case 1 will be 30 hrs,
i.e. B takes 30 hours. (1/3 of 30 hrs = 10 hrs)
So time taken by A = 30-6=24 hrs.
Quantities having relation in the form of C = A + B
If three quantities have a relation of C = A + B and quantity A is increased by x%. If we wish to maintain C as constant, then B should be reduced by and vice versa in case of a decrease.
and vice versa in case of a decrease.
Example: The saving of a person is 20% of his income. If his expenditure increases by 10% without any increase in his income, then by how much percent he has to decrease his saving?
Sol:Let us assume the income of the person is 100
So, initial savings of the person = 20% of 100 = 20
We know, Income = Expenditure + Saving
Expenditure of person = 100 – 20 = 80According to the question,
Final expenditure of person = 110% of 80 = 88
As, income is constant so final income = 100
Final Saving = 100 – 88 = 12
Successive Percentage Increase/Decrease
When two or more percentage changes are applied to a quantity consecutively, the percentage change is called a “successive percentage change.” Here, the final change is not the simple addition of two or more percentages. In a successive percentage change, a quantity is changed by some percentage, and the obtained new quantity is changed by another percentage, i.e., both the percentages are not applied to the same actual value.
1. Successive Increment Percentage Change
- When two or more increased percentage changes are applied to a quantity consecutively, the percentage change is called a “successive increment percentage change.”
- If the population of the town increased by a% and then by b%, we now have to apply the first percentage, i.e.
a%, to the initial value, then we have to apply the b%, to the resultant value obtained from the first percentage change. - Example: Let the population of the town be z. Suppose that there is a% increase in the population, then b% and then c% . What is the net percentage increase?
- Sol: Now, the first percentage increase = z + (z × a/100) = z (1 + a/100) = X
Second percentage increase = X + (X × b/100) = {z (1 + a/100) + [z × (1 + a/100) × (b/100)]}
= z (1 + a/100) (1 + b/100) = Y
Therefore, the net percentage change in the population of the town after two successive increments = {(Y – z)/z} × 100
If the value of an object x is successively increased by a%, b%, and then by c% then the final value is
x (1 + a/100) (1 + b/100) (1 + c/100)
2. Successive Decrement Percentage Change
- When two or more decreased percentage changes are applied to a quantity consecutively, the percentage change is called a “successive decrement percentage change.”
- If the price of a product is decreased by a% and then by b%, we now have to apply the first percentage, i.e., a%, to the initial value of the product. Then we have to apply the second percentage, i.e., b%, to the resultant value obtained from the first percentage change.
- Example: Let the price of the product be z. If there is decrease of a% initially then of b% and of c % afterwards, then calculate the final value?
- Sol: Now, the first percentage decrease = z – (z × a/100) = z (1 – a/100) = X
Second percentage decrease = X – (X × b/100) = {z (1 – a/100) – [z × (1 – a/100) × (b/100)]}
= z (1- a/100) (1 – b/100) = Y
Therefore, the net percentage change in the price of the product after two successive decrements = {(Y – z)/z} × 100
If the value of an object x is successively decreased by a%, b%, and then by c% the final value is
x (1 – a/100) (1 – b/100) (1 – c/100).
3. Other Successive Percentage Change
- Both percentage increment and percentage decrement can also be applied to the initial value of an object successively, and the percentage changes can also be used multiple times.
- If the value of an object x is successively changed by a%, b%, and then by c%, the final value is x (1 ± a/100) (1 ± b/100) (1 ± c/100), where the positive sign indicates an increment while the negative sign indicates a decrement.
4. Application of Percentage on Population Increase/Decrease:
- If there is an r% increase/decrease in population of a place in a year, then
- The Population of a place n years later will be

And, population of a place n years ago will be 
Percentage Change Graphic (PCG) and its Application
In Mathematics, there are many situations where one is required to work with percentage changes.
In such situations, the following thought structure (Something We can call Percentage Change Graphic) is a very useful tool.
Let us take an example , Suppose you have to increase the number 20 by 20%.
so we will visualize like
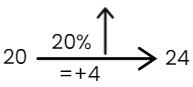
The PCG has six major applications listed and explained below:
1. Successive Changes
This is a very common situation in most of the questions.
Example 1: Suppose there is a number 30 which has two successive percentage increases (20% and 10% respectively) and at the end you have to find the final number obtained after doing successive changes?
Sol: The situation is handled in the following way using PCG:
Example 2: If A's Salary increases by 20% and then decreases by 20%. What is the net percentage change in A's Salary?
Sol:
Hence ,A's salary has gone down by 4%
Example 3: A trader marks up the price of his goods by 20%, but to a particularly haggling customer , he ends up giving a discount of 10% on the marked price. What is the percentage profit he makes?
Sol:
Hence the percentage profit is 8%
2. Product change application
- Suppose you have a product of two variables say 10 x 10.
- If the first variable changes to 11 and the second variable changes to 12, what will be the percentage change in the product?
(Note: There is a 10% increase in one part of the product and a 20% increase in the other part.) - The formula given for this situation goes as: A + B + AB/100
Hence, required % change = 10 + 20+10 x 20/100
= 30 + 2 = 32%
3. Product Constancy Application
Suppose you have a situation wherein the price of a commodity has gone up by 25%.In case you are required to keep the total expenditure on the commodity constant, you would obviously need to cut down on the consumption. By what percentage?
Well, PCG gives you the answer
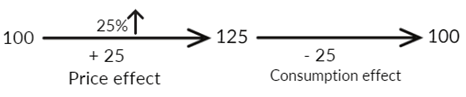
Hence the percentage drop in the consumption to offset the price increase is 20%
4. A→B→A application
- Very often we face a situation where we compare two numbers say A and B.
- In such cases, if we are given a relationship from A to B, then the reverse relationship can be determined by using PCG in much the same way as the product constancy use shown above.
Example: B's salary is 25% more than A's salary. By what percent is A's Salary less than B's salary?
Sol:
A drop of 25 on 125 gives a 20% drop
hence, A's salary is 20% less than B's.
5. Denominator Change to Ratio Change Application
- The denominator has an inverse relationship with the value of a ratio. Hence, the process used for product constancy (as explained above) can be used for calculating percentage change in the denominator.
- For instance, suppose you have to evaluate the difference between two ratios:
Ratio 1: 10/20
Ratio 2: 10/25 - As is evident, the denominator is increasing from 20 to 25 by 25%.
- If we calculate the value of the two ratios we will get
Ratio 1 = 0.5, Ratio 2 = 0.4 - Percentage change between the two ratios = (0.1/0.5)x 100
= 20% drop - This value can be obtained through PCG as
 Hence, 20% drop.
Hence, 20% drop.
6. Use of PCG to Calculate Ratio Changes
- Under normal situations, you will be faced with ratios where both numerator and denominator change. The process to handle and calculate such changes is also quite convenient if you go through PCG.
- Example: Calculate the percentage change between the ratios. Ratio 1= 10/20; Ratio 2 = 15/25
- Sol: The answer in this case is 0.5 to 0.6 (20% increase). However, in most cases calculating the values of the ratio will not be easy. The following PCG process can be used to get the answer
When 10/20 changes to 15/25, the change occurs primarily due to two reasons:
1. Change in the numerator (Numerator effect)
2. Change in the denominator (Denominator effect) By segregating the two effects and calculating the effect due to each separately. - 1. Numerator Effect
The Numerator effect on the value of the ratio is the same as the change in the numerator. Hence, to calculate the numerator effect, just calculate the percentage change in the numerator.
In this case, the numerator is clearly changing from 10 to 15 (i.e. a 50% increase.)
This signifies that the numerator effect is also 50%. - 2. Denominator Effect
As we have just seen above, the effect of a percentage change in the denominator on the value of the ratio is seen by calculating the denominators percentage change in the reverse order.
In this case, the denominator is changing from 20 so 25.
Hence, the denominator effect will be seen by going reverse from 25 to 20, ie. 20% drop.
Did You Know
- 1. If Numerator is increasing while denominator is decreasing
The net effect of the two changes will be an increase in the ratio.2. If Numerator is decreasing while denominator is increasing
The net effect of both the changes will decrease the ratio
Solved Examples
Q 1. If 5/9 is multiplied instead of 2/3 in a number, then what will be the percentage error in the calculation?
Sol: Let the number be LCM of 9 and 3 = 9
Q 2. In an examination, out of 400 students, 54% of boys and 70% of girls pass. If the total pass percentage was 60%. Find the total number of girls.
Sol: Let the number of girls be x
Thus, number of boys will be 400 – x
According to the question
Number of boys who pass = 54% of (400 – x)
Number of girls who pass = 70% of x
Total number of students who pass = 60% of 400
Thus,
60% of 400 = 54% of (400 – x) + 70% of x
240 = 216 – 0.54x + 07x
0.16x = 24
x = 150
Q 3. The population of a town increases by 20% each year. If the population of the town 3 years ago was 2500, then what is the present population of the town?
Sol: Let us assume the present population of the town is P
We know,
The population of a place n years ago will be
According to the question,
Thus, the present population of the town is 4320.
Q 4. If A earns 20% more than B, B earns 25% more than C, C earns 16.67% less than D, then A earns how much percent of D?
Sol: We know,
According to the question,
Combining all the above equation,
Q 5. A 20% ethanol solution is mixed with another ethanol solution, say, S of unknown concentration in the proportion 1:3 by volume. This mixture is then mixed with an equal volume of 20% ethanol solution. If the resultant mixture is a 31.25% ethanol solution, then the unknown concentration of S is
A) 30%
B) 40%
C) 50%
D) 60%
Ans. Option 'c' is correct.
Sol: Let the volume of the rst and the second solution be 100 and 300.
When they are mixed, quantity of ethanol in the mixture = (20 + 300S)
Let this solution be mixed with equal volume i.e. 400 of third solution in which the strength of ethanol is 20%.
So, the quantity of ethanol in the final solution = (20 + 300S + 80) = (300S + 100)
It is given that, 31.25% of 800 = (300S + 100)
or 300S + 100
S = 1/2 = 50%
Hence, 50 is the correct answer.
Q 6. The salaries of Ramesh, Ganesh and Rajesh were in the ratio 6:5:7 in 2010, and in the ratio 3:4:3 in 2015. If Ramesh’s salary increased by 25% during 2010-2015, then the percentage increase in Rajesh’s salary during this period is closest to
A) 10
B) 7
C) 9
D) 8
Ans: Option 'b' is correct.
Sol: Let the salaries of Ramesh, Ganesh and Rajesh in 2010 be 6x, 5x, 7x respectively
Let the salaries of Ramesh, Ganesh and Rajesh in 2015 be 3y, 4y, 3y respectively
It is given that Ramesh’s salary increased by 25% during 2010-2015,3y = 1.25*6x y=2.5x
Percentage increase in Rajesh's salary = 7.5-7/7=0.07 =7%
|
191 videos|133 docs|110 tests
|
FAQs on Important Formulas for CAT Percentages
| 1. What are percentages and how are they used in everyday life? |  |
| 2. How do you calculate a percentage step-by-step? |  |
| 3. What is the difference between percentage change and percentage point change? |  |
| 4. How do you calculate successive percentage increases or decreases? |  |
| 5. What is Percentage Change Graphic (PCG) and how is it useful? |  |











 Hence ,A's salary has gone down by 4%
Hence ,A's salary has gone down by 4% Hence the percentage profit is 8%
Hence the percentage profit is 8% A drop of 25 on 125 gives a 20% drop
A drop of 25 on 125 gives a 20% drop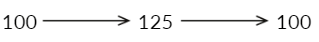 Hence, 20% drop.
Hence, 20% drop.
























