Important Formulas: Arithmetic Progression | Quantitative for GMAT PDF Download
Logarithm
- If a is a positive real number, other than 1 and am = x, then we write: m = loga x and we say that the value of log x to the base a is m.
- Examples: (i) 103 1000 ⇒ log10 1000 = 3.
(ii) 34 = 81 ⇒ log3 81 = 4.
(iv) (. 1)2 = 01 ⇒ log(.1) .01 = 2.
Properties of Logarithms
1. log a (xy) = loga x + loga y
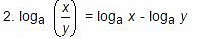
3. logx x = 1
4. loga 1 = 0
5. loga (xn) = n(loga x)
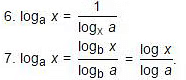
Common Logarithms
- Logarithms to the base 10 are known as common logarithms.
- The logarithm of a number contains two parts, namely 'characteristic' and 'mantissa'.
1. Characteristic
The internal part of the logarithm of a number is called its characteristic.
Case I: When the number is greater than 1.
- In this case, the characteristic is one less than the number of digits in the left of the decimal point in the given number.
Case II: When the number is less than 1.
- In this case, the characteristic is one more than the number of zeros between the decimal point and the first significant digit of the number and it is negative.
- Instead of -1, -2 etc. we write
 (two bar), etc.
(two bar), etc.
Examples:
2. Mantissa:
The decimal part of the logarithm of a number is known is its mantissa. For mantissa, we look through log table.
Question 1: If log2X + log4X = log0.25√6 and x > 0, then x is:
A. 6-1/6
B. 61/6
C. 3-1/3
D. 61/3
Correct Answer is Option (A).
- log2x + log4x = log0.25√6
We can rewrite the equation as:
⇒ log2x * 3 = 2log0.25√6
⇒ log2x3 = -log46
⇒ ⇒
⇒
⇒ 2log2x3 = -log26 - 2log2x3 + log26 = 0
log26X6 = 0 - 6x6 = 1
x6 = 1/6
- The question is "If log2X + log4X = log0.25 √6 and x > 0, then x is"
- Hence, the answer is "6-1/6".
Question 2: log9 (3log2 (1 + log3 (1 + 2log2x))) = 1/2. Find x.
A. 4
B. 1/2
C. 1
D. 2
Correct Answer is Option (D).
log9 (3log2 (1 + log3 (1 + 2log2x)) = 1/2
3log2(1 + log3(1 + 2log2x)) = 91/2 = 3
log2(1 + log3(1 + 2log2x) = 1
1 + log3(1 + 2log2x) = 2
log3(1 + 2log2x) = 1
1 + 2log2x = 3
2log2x = 2
log2x = 1
x = 2
The question is "Find x."
Hence, the answer is "2".
Question 3: If 22x+4 – 17 × 2x+1 = –4, then which of the following is true?
A. x is a positive value
B. x is a negative value
C. x can be either a positive value or a negative value
D. None of these
Correct Answer is Option (C).
2x+4 – 17 * 2x+1 = – 4
=> 2x+1 = y
22x+2 = y2
22(22x+2) – 17 * 2x+1 = –4
4y2 – 17y + 4 = 0
4y2 – 16y – y + y = 0
4y (y – 4) – 1 (y – 4) = 0
y = 1/4 or 4
2x+1 = 1/4 or 4
⇒ x + 1 = 2 or – 2
x = 1 or – 3
The question is "which of the following is true?"
Hence, the answer is "x can be either a positive value or a negative value".
Logarithmic Series
Definition
An expansion for loge (1 + x) as a series of powers of x which is valid only, when |x|<1.
Expansion of logarithmic series
Expansion of loge (1 + x) if |x|<1 then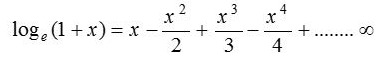
Replacing x by −x in the logarithmic series, we get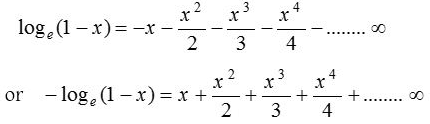
Some Important results from logarithmic series
(1) 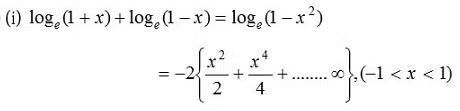

(2) The series expansion of loge (1 + x) may fail to be valid, if |x| is not less than 1. It can be proved that the logarithmic series is valid for x = 1. Putting x = 1 in the logarithmic series.
We get,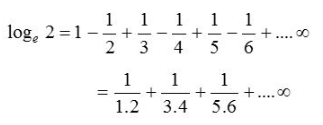
(3) When x = −1, the logarithmic series does not have a sum. This is in conformity with the fact that log(1 – 1) is not a finite quantity.
Difference between the exponential and logarithmic series
- In the exponential series
 all the terms carry positive signs whereas in the logarithmic series
all the terms carry positive signs whereas in the logarithmic series  the terms are alternatively positive and negative
the terms are alternatively positive and negative - In the exponential series the denominator of the terms involve factorial of natural numbers. But in the logarithmic series the terms do not contain factorials.
- The exponential series is valid for all the values of x. The logarithmic series is valid, when |x|< 1.
|
115 videos|106 docs|113 tests
|
FAQs on Important Formulas: Arithmetic Progression - Quantitative for GMAT
| 1. What are the properties of logarithms? |  |
| 2. What are the important formulas related to arithmetic progression? |  |
| 3. How do you use the product rule of logarithms? |  |
| 4. How do you find the nth term of an arithmetic progression? |  |
| 5. How do you find the sum of the first n terms of an arithmetic progression? |  |

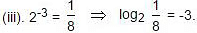
 (two bar), etc.
(two bar), etc.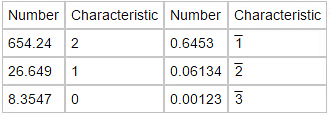
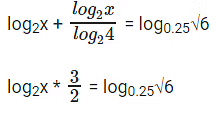
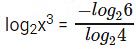 ⇒
⇒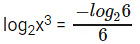
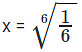
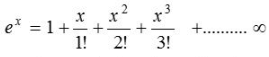 all the terms carry positive signs whereas in the logarithmic series
all the terms carry positive signs whereas in the logarithmic series 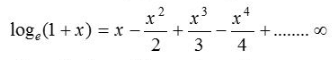 the terms are alternatively positive and negative
the terms are alternatively positive and negative
















