GMAT Exam > GMAT Notes > Quantitative for GMAT > Important Formulas: Exponents
Important Formulas: Exponents | Quantitative for GMAT PDF Download
Exponents Formulas
There are various laws of exponents that you should practice and remember in order to thoroughly understand the exponential concepts. The following exponent law is detailed with examples on exponential powers and radicals and roots.
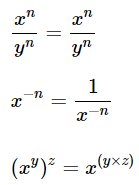
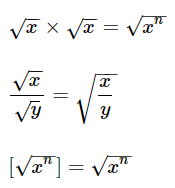
Properties of Exponents and Radicals
Example1: If m2+n2+o2 = mn+no+om, simplify [ym/yn]m-n × [yn/yo]n-o × [yo/ym]o-m
Sol:
Using ma/nb = ma-b, we obtain
→ (ym-n)m-n×(yn-o)n-o×(yo-m)o-m
Using the formula
(m-n)2 = m2+n2-2mn in the exponent,
→y(m²+n²−2mn) * y(m²+o²−2no) * y(o²+m²−2om)
Doing the Math
ma.mb=ma+b
→ y(m²+n²−2mn+n²+o²−2no+o²+m²−2om)
→ y2(m²+n²+o²−(mn+no+om))
→ y2(0)2(0)
→ y0=1
Example 2: Find y if 32y-1+32y+1=270
Sol: We will first take out a term in common, with which we obtain
→ 32y-1(1+32)
See that here, we are using the formula for any non-integer am+n = am. an in expressing 32y+1 as a product of 32y-1 and 32.
32y-1(10)=270
32y-1=27
32y-1=33
2y−1=3
y = 2.
The document Important Formulas: Exponents | Quantitative for GMAT is a part of the GMAT Course Quantitative for GMAT.
All you need of GMAT at this link: GMAT
|
127 videos|154 docs|111 tests
|
FAQs on Important Formulas: Exponents - Quantitative for GMAT
| 1. What is the formula for finding the value of an exponent? |  |
Ans. The formula for finding the value of an exponent is expressed as a^b, where 'a' is the base and 'b' is the exponent. This means that the base 'a' is multiplied by itself 'b' times.
| 2. How do you simplify an exponential expression? | |
Ans. To simplify an exponential expression, you can use the following rules:
- When multiplying powers with the same base, add their exponents: a^m * a^n = a^(m + n).
- When dividing powers with the same base, subtract their exponents: a^m / a^n = a^(m - n).
- When raising a power to another power, multiply the exponents: (a^m)^n = a^(m * n).
| 3. What is the power of a power rule in exponents? | |
Ans. The power of a power rule states that when raising a power to another power, you multiply the exponents. This rule is expressed as (a^m)^n = a^(m * n). For example, (2^3)^2 = 2^(3 * 2) = 2^6 = 64.
| 4. How do you simplify expressions with negative exponents? | |
Ans. To simplify expressions with negative exponents, you can use the following rule: a^(-n) = 1 / a^n. This means that any term with a negative exponent can be rewritten as its reciprocal with a positive exponent. For example, 2^(-3) = 1 / 2^3 = 1 / 8.
| 5. How do you simplify expressions with zero exponents? | |
Ans. When an exponent is zero, the simplified value of the expression is always 1. This means that any base raised to the power of zero equals 1. For example, 5^0 = 1.
About this Document
4.96/5
Rating
Sep 05, 2025
Last updated
Related Exams
Document Description: Important Formulas: Exponents for GMAT 2025 is part of Quantitative for GMAT preparation.
The notes and questions for Important Formulas: Exponents have been prepared according to the GMAT exam syllabus. Information about Important Formulas: Exponents covers topics
like and Important Formulas: Exponents Example, for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Formulas: Exponents.
Introduction of Important Formulas: Exponents in English is available as part of our Quantitative for GMAT
for GMAT & Important Formulas: Exponents in Hindi for Quantitative for GMAT course.
Download more important topics related with notes, lectures and mock test series for GMAT
Exam by signing up for free. GMAT: Important Formulas: Exponents | Quantitative for GMAT
Description
Full syllabus notes, lecture & questions for Important Formulas: Exponents | Quantitative for GMAT - GMAT | Plus excerises question with solution to help you revise complete syllabus for Quantitative for GMAT | Best notes, free PDF download
Information about Important Formulas: Exponents
In this doc you can find the meaning of Important Formulas: Exponents defined & explained in the simplest way possible. Besides explaining types of
Important Formulas: Exponents theory, EduRev gives you an ample number of questions to practice Important Formulas: Exponents tests, examples and also practice GMAT
tests
Related Searches
Semester Notes
,study material
,Important questions
,video lectures
,Exam
,shortcuts and tricks
,Important Formulas: Exponents | Quantitative for GMAT
,Important Formulas: Exponents | Quantitative for GMAT
,Important Formulas: Exponents | Quantitative for GMAT
,Summary
,Previous Year Questions with Solutions
,Extra Questions
,Objective type Questions
,past year papers
,Viva Questions
,ppt
,MCQs
,practice quizzes
,mock tests for examination
,Sample Paper
,Free
;
Additional Information about Important Formulas: Exponents for GMAT Preparation
Important Formulas: Exponents Free PDF Download
The Important Formulas: Exponents is an invaluable resource that delves deep into the core of the GMAT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Formulas: Exponents now and kickstart your journey towards success in the GMAT exam.
Importance of Important Formulas: Exponents
The importance of Important Formulas: Exponents cannot be overstated, especially for GMAT aspirants.
This document holds the key to success in the GMAT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Formulas: Exponents Notes
Important Formulas: Exponents Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Formulas: Exponents.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Formulas: Exponents Notes on EduRev are your ultimate resource for success.
Important Formulas: Exponents GMAT Questions
The "Important Formulas: Exponents GMAT Questions" guide is a valuable resource for all aspiring students preparing for the
GMAT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Formulas: Exponents on the App
Students of GMAT can study Important Formulas: Exponents alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Formulas: Exponents,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Formulas: Exponents is prepared as per the latest GMAT syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily