Important Formulas: Linear Equations | Quantitative Aptitude (Quant) - CAT PDF Download
Formulas & Definitions for Linear Equations
- A linear equation is an algebraic equation in which each term has an exponent of one and the graphing of the equation results in a straight line.
- Standard form of linear equation is y = mx + b. Where, x is the variable and y, m, and b are the constants.
Forms of Linear Equations
There are mainly 3 forms of Linear Equation:
1. Standard Form
The standard form of a linear equation is typically written as: Ax + By = C
Where:
- A and B are coefficients (constants) representing the coefficients of x and y terms, respectively.
- C is a constant term.
The standard form requires that A and B are both integers and that A is non-negative. Also, A and B should not have any common factors other than 1. This form is commonly used in algebraic manipulation and solving systems of linear equations.
2. Slope-Intercept Form
The slope-intercept form of a linear equation is written as:
y = mx + b
Where:
- m is the slope of the line, representing the rate of change between y and x.
- b is the y-intercept, which is the value of y when x is equal to 0. It represents the point where the line intersects the y-axis.
This form is particularly useful for graphing linear equations and quickly identifying the slope and y-intercept of the line.
3. Point-Slope Form
The point-slope form of a linear equation is given by:
y − y1 = m(x − x1)
Where:
- m is the slope of the line, as explained in the slope-intercept form.
- (x1 ,y1) represents the coordinates of a point on the line.
This form is useful when you know a specific point on the line and its slope, allowing you to write the equation directly without having to calculate the y-intercept.
Linear equations in one variable
- A Linear Equation in one variable is defined as ax + b = 0
- Where, a and b are constant, a ≠ 0, and x is an unknown variable
- The solution of the equation ax + b = 0 is x = – b/a. We can also say that – b/a is the root of the linear equation ax + b = 0.
Linear equations in two variable
- A Linear Equation in two variables is defined as ax + by + c = 0
- Where a, b, and c are constants and also, both a and b ≠ 0
Linear equations in three variable
- A Linear Equation in three variables is defined as ax + by + cz = d
- Where a, b, c, and d are constants and also, a, b and c ≠ 0
Formulas and Methods to solve Linear equations
Substitution Method
- Step 1: Solve one of the equations either for x or y.
- Step 2: Substitute the solution from step 1 into the other equation.
- Step 3: Now solve this equation for the second variable.
Elimination Method
- Step 1: Multiply both the equations with such numbers to make the coefficients of one of the two unknowns numerically same.
- Step 2: Subtract the second equation from the first equation.
- Step 3: In either of the two equations, substitute the value of the unknown variable. So, by solving the equation, the value of the other unknown variable is obtained.
Cross-Multiplication Method
Suppose there are two equation,
P1x+Q1Y = r1 .........(1)
P2x + Q2Y = 12 ........(2)
Multiply Equation (1) with p2
Multiply Equation (2) with p1
P1P2x + Q1P2Y = r1P2
P1P2X + P1Q2Y = P1r2
Subtracting,
Q1P2Y-P1Q2Y = r1P2-P1r2
or, y (Q1 P2- Q2P1) = r2P1 - r1P2 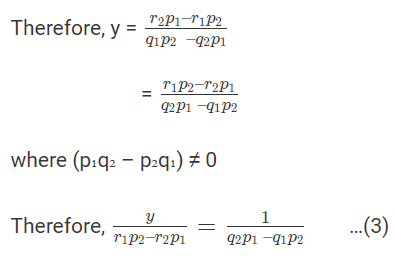
Multiply Equation (1) with q2
Multiply Equation (2) with q1
P1Q2x + Q1Q2Y = r1Q2
Q1P2x + Q1Q2Y = Q1r2
Subtracting, 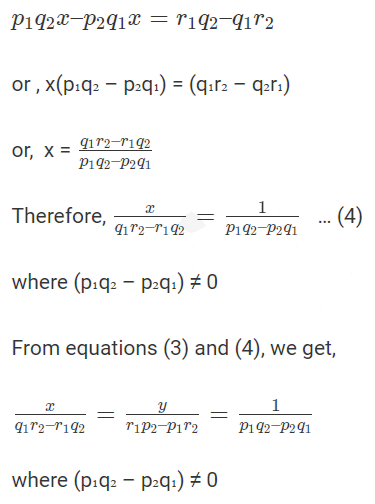
From equations (3) and (4), we get,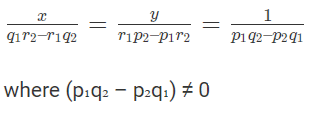
Note: Shortcut to solve this equation will be written as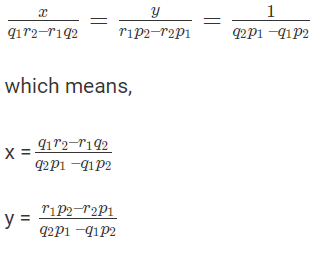
Important Formulas of Linear Equation & key points to Remember
Suppose, there are two linear equations: a1x + b1y = c1 and a2x + b2y = c2
Then,
Questions on Formulas of Linear Equation
Q1: What is the slope-intercept form of the equation of a line?
(a) y = mx + b
(b) y = mx − b
(c) y = bx + m
(d) y =bx − m
Ans: (a)
Sol: The slope-intercept form of a linear equation is y = mx + b, where m represents the slope and b represents the y-intercept.
Q2: How can you eliminate fractions from a linear equation?
(a) Multiply both sides of the equation by a common denominator
(b) Divide both sides of the equation by a common denominator
(c) Add both sides of the equation by a common denominator
(d) Subtract both sides of the equation by a common denominator
Ans: (a)
Explanation: To eliminate fractions from a linear equation, multiply both sides of the equation by a common denominator. This process will clear the fractions and make the equation easier to solve.
|
167 videos|238 docs|95 tests
|
FAQs on Important Formulas: Linear Equations - Quantitative Aptitude (Quant) - CAT
| 1. What is a linear equation in one variable, and how is it structured? |  |
| 2. How do you solve a linear equation in two variables? |  |
| 3. What are the key methods used to solve systems of linear equations? |  |
| 4. What are some important formulas related to linear equations that students should remember? |  |
| 5. What is the significance of the slope in a linear equation? |  |
















