Important Formulas: Mixture and Alligations | Quantitative for GMAT PDF Download
| Table of contents |

|
| Alligation |

|
| Mixture |

|
| What is a Mean Price? |

|
| Criss-Cross Method |

|
| Rule of Constant |

|
| Conclusion |

|
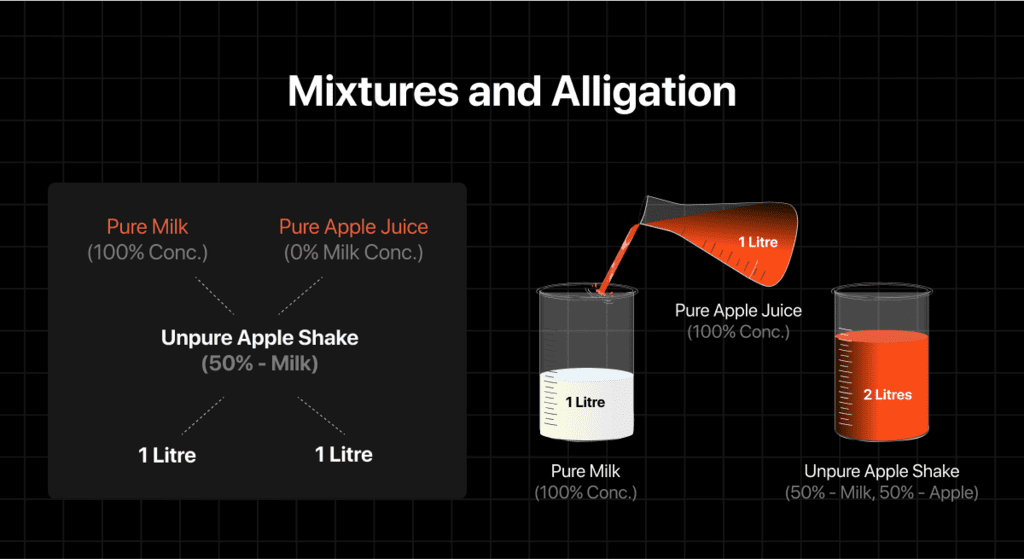
Alligation
Alligation is the rule used to determine the ratio in which two ingredients (X and Y) of different prices are mixed to form a mixture with a given mean price.
Formula:
When two ingredients, X and Y, with prices p and q respectively, are mixed to form a mixture with mean price M, the ratio in which they are mixed is given by:
(Cheaper quantity) : (Dearer quantity) = (d – m) : (m – c)
d = Price of the dearer ingredient
c = Price of the cheaper ingredient
m = Mean price of the mixture
Mixture
A mixture involves combining two or more ingredients to obtain a desired quantity or quality. The quantities involved can be expressed in ratios or percentages.
For example: Mixing two varieties of sugar to form a new variety is an example of a mixture.
What is a Mean Price?
The mean price is the cost of a unit quantity of the mixture. It is essentially the average price of the ingredients after they have been mixed together, weighted by their quantities.
Formulas to Solve Mixture and Alligations
1. Formula 1: Alligation with Two Commodities
When two commodities with different prices are mixed, the following formula applies: (Cheaper quantity) : (Dearer quantity) = (d – m) : (m – c)
(Cheaper quantity) : (Dearer quantity) = (d – m) : (m – c)
Where:
d = Price of the dearer commodity
m = Mean price of the mixture
c = Price of the cheaper commodity
2. Formula 2: Successive Replacements of Liquid
Consider a container that contains x units of liquid A, and y units of it are removed and replaced by water. If this operation is repeated n times, the amount of pure liquid remaining is given by the formula:
Where:
x = Initial quantity of liquid A
y = Quantity removed and replaced by water
n = Number of times the operation is repeated
3. Formula 3: Quantity of Pure Liquid After n Successive Operations
Calculate quantity of pure Liquid after ‘n’ successive operations,
If a container contains ‘x’ units of pure liquid , and we replace the liquid with ‘y’ units of water ,
Then after ‘n’ successive operations, the units of pure liquid left is ,
After n operations, the quantity of pure liquid 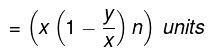
Criss-Cross Method
Some aspirants use the above method in different format, which we call criss-cross method. Below is the format:
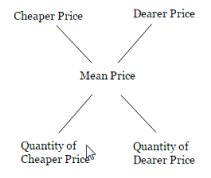
The working is, we take the positive difference of mean price and cheaper price and write the difference in the place of Quantity of dearer price. Similarly, take the positive difference of mean price and dearer price and write the difference in the place of Quantity of cheaper price.
Rule of Constant
The Rule of Constant is useful in problems where the quantity of one ingredient in the mixture remains constant while the other ingredient is added or replaced. This rule helps in solving problems where percentages change but the amount of one ingredient remains unchanged.
Method 1: School textbook approach
We assume that the quantity of water added to be x litres. The quantity of milk in the existing solution is 30% of 40 = 12 litres, with the addition of water, the quantity of new solution becomes (40 + x) litres. As per the problem, the percentage of milk in new solution should be 15 %. we will get x = 40.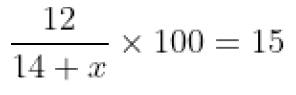 Method 2: Rule of Alligation.
Method 2: Rule of Alligation.
We assume that the two solutions of milk and water are added to get the new solution and apply the approach we used in Example 3.
Taking milk as the common element in both the solutions, we have 30% milk in first and 0% milk in the second solution (i.e. pure water). On mixing them, we got 15% milk in the final solution. Therefore,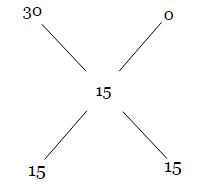
Or the ratio of the quantity of first and second solution should be 15:15 = 1:1
Hence, 40 litres of pure water should be mixed to get the desired new solution.
Method 3: Rule of Constant
In this rule, we target the element in the mixture whose amount does not change but its percentage changes because of the change in the total amount of the mixture.
As we calculated above, the quantity of milk in the first solution is 12 litres, and it will remain same in the new solution as well. That is,
12 liters = 30% of the first solution =15% of the new solution
Conclusion
Understanding the Mixture and Alligation concepts and applying the formulas and methods above will help you tackle a wide range of problems efficiently. Mastering these techniques will allow you to solve problems involving mixtures, alligation, and successive replacements with confidence.
|
127 videos|154 docs|111 tests
|
FAQs on Important Formulas: Mixture and Alligations - Quantitative for GMAT
| 1. What is alligation in the context of mixtures? |  |
| 2. How is alligation useful in real life scenarios? |  |
| 3. How do you solve an alligation problem? |  |
| 4. Can alligation be used for more than two ingredients? |  |
| 5. Are there any limitations or drawbacks of using alligation? |  |




















