Important Formulas: Patterns in Mathematics | Maths for Class 6 (Ganita Prakash) - New NCERT PDF Download
1. Patterns in Mathematics: Mathematics involves recognizing patterns in numbers, shapes, and daily life. Examples include the days of the week repeating in a cycle.
2. The branch of Mathematics that studies patterns in whole numbers is called number theory.
3. Number Sequences: Ordered lists of numbers that follow a specific rule or pattern.
For example: In the odd numbers sequence, each number is generated by adding 2 to the previous number, starting from 1.
4. Visualizing number sequences can make patterns easier to understand.
5. Square numbers can be shown as dots arranged in a perfect square; 4 dots form a 2x2 square, and 9 dots form a 3x3 square.

6. Triangular numbers can be represented as dots forming a triangle; for instance, 1, 3, 6, 10, and 15 dots form triangles with 1, 2, 3, 4, and 5 rows, respectively.

7. Visualizing these sequences helps to see how numbers relate to each other, such as 36 being both a square (6x6) and a triangular number.

8. Different number sequences can be related in intriguing ways.
For example, if you add consecutive odd numbers, like 1, 1+3, 1+3+5, and so on, the result always forms a square number.
9. The visualization helps in understanding and calculating the sums related to square numbers.
For instance, adding 1 dot forms a 1x1 square, adding 3 dots forms a 2x2 square, adding 5 more forms a 3x3 square, and so on.

10. In mathematics, patterns can be found in shapes as well. These patterns are explored in geometry and can involve shapes in one, two, or three dimensions.
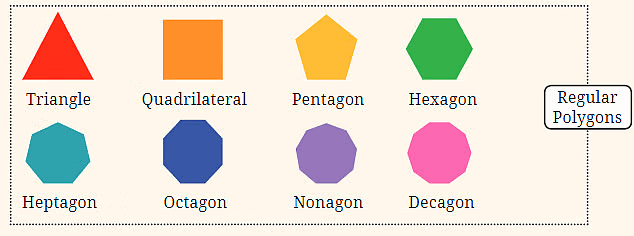
11. Regular Polygons: This sequence starts with polygons having equal sides and angles. It begins with a triangle (3 sides), then a quadrilateral (4 sides), followed by a pentagon (5 sides), and so on. Each step adds one more side to the shape.
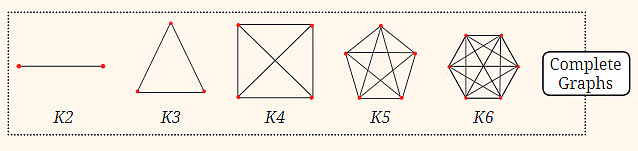
12. Complete Graphs: This sequence involves graphs where each point is connected to every other point. It starts with two points connected by a line, progresses to three points forming a triangle, four points forming a square with diagonals, and continues with increasing connections.
13. Stacked Squares: This sequence shows squares stacked on top of each other, starting from a single square and growing into larger squares made up of smaller squares.
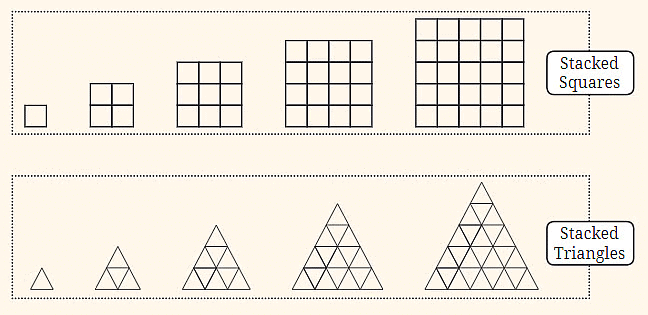
14. Stacked Triangles: This sequence involves triangles stacked to form larger triangles.
15. Koch Snowflake: This is a fractal shape beginning with a simple triangle. At each step, smaller triangles are added to each side, creating a more complex pattern resembling a snowflake.

16. Relationships: Stacked Squares are related to square numbers, where each step adds another row and column of squares. Complete Graphs relate to the number of connections, similar to triangular numbers.
Recognizing these connections helps in understanding both geometric and arithmetic patterns.
|
2 videos|74 docs|19 tests
|
FAQs on Important Formulas: Patterns in Mathematics - Maths for Class 6 (Ganita Prakash) - New NCERT
| 1. What are some common patterns in mathematics that students learn in Class 6? |  |
| 2. How can recognizing patterns in mathematics help students solve problems more effectively? |  |
| 3. Why is it important for students to understand patterns in mathematics? |  |
| 4. How can teachers help students recognize and analyze patterns in mathematics? |  |
| 5. Can patterns in mathematics be found in everyday life outside of the classroom? |  |
|
2 videos|74 docs|19 tests
|

|
Explore Courses for Class 6 exam
|

|

















