Important Formulas: Quadratic Equations | Quantitative Aptitude (Quant) - CAT PDF Download
Quadratic equations are a key part of the CAT exam’s quantitative aptitude section. A clear understanding of their forms, roots, and properties helps in solving problems quickly and accurately, making them essential for exam success.
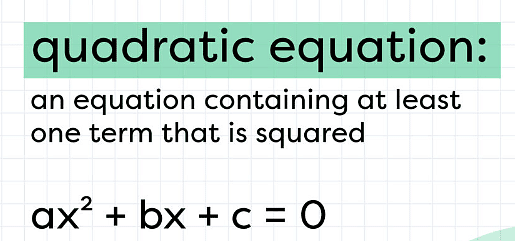
What are Quadratic Equations
- A quadratic equation is a mathematical expression of the second degree in the variable x.
- The typical representation of a quadratic equation is ax 2 + bx + c = 0, where a, b, and c are constants, x is the variable, and a is non-zero ( a ≠ 0 ).
- In a quadratic equation, the coefficient of x 2 must be non-zero for it to be classified as such.
- Quadratic equations can be written in various forms, not just the standard one.
Roots of the Quadratic Equation
- When we talk about the roots of a quadratic equation, we are referring to the two values of x that satisfy the equation. These values are also known as the zeros of the equation.
- For example, in the quadratic equation x 2 - 3x - 4 = 0, the roots are x = 4 and x = -1. This is because both of these values make the equation true. To see this:
At x = -1. (-1) 2 - 3(-1) - 4 = 1 + 3 - 4 = 0. At x = 4. (4) 2 - 3(4) - 4 = 16 - 12 - 4 = 0. - There are various methods to find the roots of a quadratic equation, and one of the most effective ways is by using the quadratic formula.
Quadratic Formula

Example: Let us find the roots of the same equation that was mentioned in the earlier section x2 - 3x - 4 = 0 using the quadratic formula.
Sol: a = 1, b = -3, and c = -4.
x = [-b ± √(b2 - 4ac)]/2a
= [-(-3) ± √((-3)2 - 4(1)(-4))]/2(1)
= [3 ± √25] / 2
= [3 ± 5] / 2
= (3 + 5)/2 or (3 - 5)/2
= 8/2 or -2/2
= 4 or -1 are the roots.`
Sum and Product of Roots of a Quadratic Equation
- Sum of the Roots: α + β = -b/a = - Coefficient of x/ Coefficient of x2
- Product of the Roots: αβ = c/a = Constant term/ Coefficient of x2
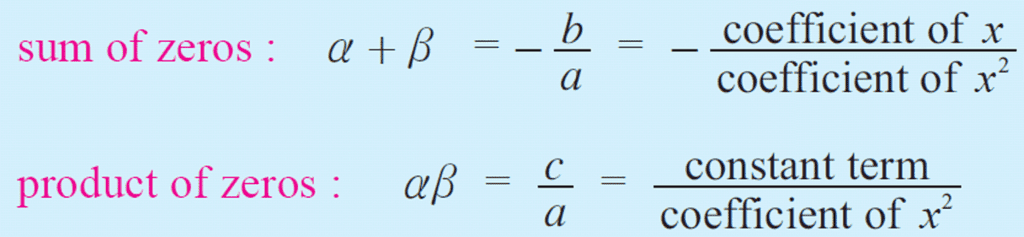
Writing Quadratic Equations Using Roots
- The quadratic equation can also be formed for the given roots of the equation. If α, β, are the roots of the quadratic equation, then the quadratic equation is as follows.
- x2 - (α + β)x + αβ = 0
- Example: What is the quadratic equation whose roots are 4 and -1?
- Solution: It is given that α = 4 and β = -1. The corresponding quadratic equation is found by:
x2 - (α + β)x + αβ = 0
x2 - (α + β)x + αβ = 0
x2 - (4 - 1)x + (4)(-1) = 0
x2 - 3x - 4 = 0
Key Formulas
A quadratic equation is expressed as ax2 + bx + c = 0, where a, b, and c are constants, x is the variable, and a ≠ 0. The values of x that satisfy this equation are called the roots, which can be found using the quadratic formula, attributed to the ancient Indian mathematician Sridharacharya:
Quadratic Formula:
x = [-b ± √(b2 - 4ac)] / (2a)
Let the roots of the equation be denoted by α and β. The following relationships hold:
- Sum of Roots: α + β = -b/a (i.e., -Coefficient of x / Coefficient of x2)
- Product of Roots: αβ = c/a (i.e., Constant term / Coefficient of x2)
Additional Properties
- If c/a = 1, the roots are reciprocals of each other (i.e., α = 1/β).
- If b = 0, the equation becomes ax2 + c = 0, and the roots are x = ±√(-c/a), which are opposite in sign.
- The minimum or maximum value of the quadratic expression ax2+ bx + c occurs at x = -b/(2a):
- If a > 0, the minimum value is (4ac - b2)/(4a).
- If a < 0, the maximum value is (4ac - b2)/(4a).

Nature of Roots
The nature of the roots of a quadratic equation depends on the discriminant, defined as:
Discriminant: D = b2 - 4ac
The value of D determines the nature of the roots as follows:
- D > 0 and a perfect square: The roots are real, rational, and unequal.
- D > 0 and not a perfect square: The roots are real, irrational, and unequal.
- D = 0: The roots are real, equal, and given by x = -b/(2a).
- D < 0: The roots are complex conjugates of the form p ± iq, where p and q are real numbers determined by the quadratic formula.

Signs of the Roots
Let P be the product of roots and S be their sum
- P > 0, S > 0 : Both roots are positive
- P > 0, S < 0 : Both roots are negative
- P < 0, S > 0 : Numerical smaller root is negative and the other root is positive
- P < 0, S < 0 : Numerical larger root is negative and the other root is positive
- Minimum and maximum values of a2 + bx + c = 0
- If a > 0: minimum value
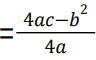 and occurs at x = -b/2a
and occurs at x = -b/2a - If a < 0: maximum value =
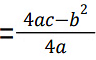 and occurs at = -b/2a
and occurs at = -b/2a 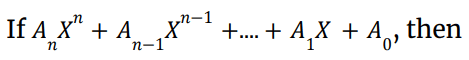
- Sum of the roots =
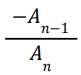
- Sum of roots taken two at a time =
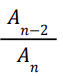
- Sum of roots taken three at a time
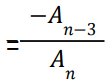 and so on, product of the roots
and so on, product of the roots 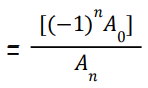
|
167 videos|229 docs|95 tests
|
FAQs on Important Formulas: Quadratic Equations - Quantitative Aptitude (Quant) - CAT
| 1. What are the important formulas related to quadratic equations? |  |
| 2. How can you determine the signs of the roots of a quadratic equation? |  |
| 3. How can you find a quadratic equation given its roots? |  |
| 4. What is the significance of quadratic equations in real-life applications? |  |
| 5. How can one solve quadratic equations using the quadratic formula? |  |





















