Important Formulas: Trigonometry | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
Trigonometry Formulas
When we learn about trigonometric formulas, we consider them for right-angled triangles only. In a right-angled triangle, we have 3 sides namely – Hypotenuse, Opposite side (Perpendicular), and Adjacent side (Base). The longest side is known as the hypotenuse, the side opposite to the angle is perpendicular and the side where both hypotenuse and opposite side rests is the adjacent side.
Basic Trigonometric Function Formulas
There are basically 6 ratios used for finding the elements in Trigonometry. They are called trigonometric functions. The six trigonometric functions are sine, cosine, secant, cosecant, tangent and cotangent.
By using a right-angled triangle as a reference, the trigonometric functions and identities are derived:
- sin θ = Opposite Side/Hypotenuse
- cos θ = Adjacent Side/Hypotenuse
- tan θ = Opposite Side/Adjacent Side
- sec θ = Hypotenuse/Adjacent Side
- cosec θ = Hypotenuse/Opposite Side
- cot θ = Adjacent Side/Opposite Side
Reciprocal Identities
The Reciprocal Identities are given as:
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
All these are taken from a right-angled triangle. When the height and base side of the right triangle are known, we can find out the sine, cosine, tangent, secant, cosecant, and cotangent values using trigonometric formulas. The reciprocal trigonometric identities are also derived by using the trigonometric functions.
Trigonometry Table
Below is the table for trigonometry formulas for angles that are commonly used for solving problems.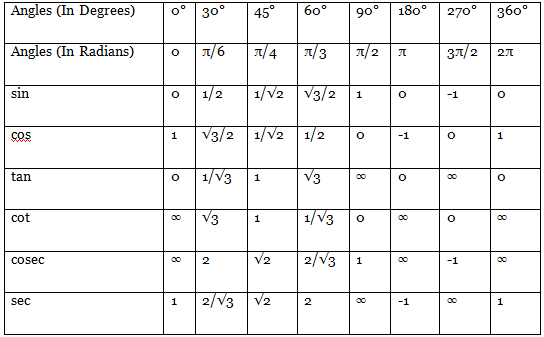
Periodicity Identities (in Radians)
These formulas are used to shift the angles by π/2, π, 2π, etc. They are also called co-function identities.
- sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
- sin (π/2 + A) = cos A & cos (π/2 + A) = – sin A
- sin (3π/2 – A) = – cos A & cos (3π/2 – A) = – sin A
- sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A
- sin (π – A) = sin A & cos (π – A) = – cos A
- sin (π + A) = – sin A & cos (π + A) = – cos A
- sin (2π – A) = – sin A & cos (2π – A) = cos A
- sin (2π + A) = sin A & cos (2π + A) = cos A
All trigonometric identities are cyclic in nature. They repeat themselves after this periodicity constant. This periodicity constant is different for different trigonometric identities. tan 45° = tan 225° but this is true for cos 45° and cos 225°. Refer to the above trigonometry table to verify the values.
Cofunction Identities (in Degrees)
The co-function or periodic identities can also be represented in degrees as:
- sin(90°−x) = cos x
- cos(90°−x) = sin x
- tan(90°−x) = cot x
- cot(90°−x) = tan x
- sec(90°−x) = cosec x
- cosec(90°−x) = sec x
Sum & Difference Identities
- sin(x+y) = sin(x)cos(y)+cos(x)sin(y)
- cos(x+y) = cos(x)cos(y)–sin(x)sin(y)

- sin(x–y) = sin(x)cos(y)–cos(x)sin(y)
- cos(x–y) = cos(x)cos(y) + sin(x)sin(y)

Double Angle Identities
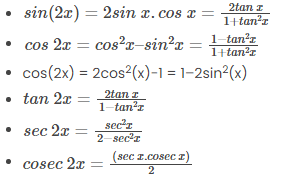
Triple Angle Identities
- Sin 3x = 3sin x – 4sin3x
- Cos 3x = 4cos3x-3cos x

Half Angle Identities

Also,




Product identities

Sum to Product Identities
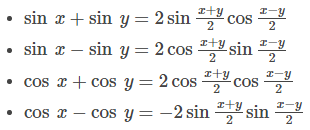
Inverse Trigonometry Formulas
- sin-1 (–x) = – sin-1 x
- cos-1 (–x) = π – cos-1 x
- tan-1 (–x) = – tan-1 x
- cosec-1 (–x) = – cosec-1 x
- sec-1 (–x) = π – sec-1 x
- cot-1 (–x) = π – cot-1 x
What is Sin 3x Formula?
Sin 3x is the sine of three times of an angle in a right-angled triangle, which is expressed as:
Sin 3x = 3sin x – 4sin3x
|
1365 videos|1312 docs|1010 tests
|
FAQs on Important Formulas: Trigonometry - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What are the basic trigonometric ratios? |  |
| 2. How do I find the values of trigonometric ratios for special angles? |  |
| 3. How can I find the values of trigonometric ratios for any angle? |  |
| 4. What is the Pythagorean identity in trigonometry? |  |
| 5. How are trigonometric ratios used in real-life applications? |  |
|
1365 videos|1312 docs|1010 tests
|

|
Explore Courses for SSC CGL exam
|

|




















