Important Questions: Linear Inequalities | Mathematics (Maths) Class 11 - Commerce PDF Download
Q1: The cost and revenue functions of a product are given by C(x) = 20 x + 4000 and R(x) = 60x + 2000, respectively, where x is the number of items produced and sold. How many items must be sold to realise some profit?
Ans: Given that,
Cost, C(x) = 20 x + 4000
Revenue, R(x) = 60x + 2000
We know that, profit = Revenue – Cost
Now, substitute the given data in the above formula,
Profit = R(x) – C(x)
Profit = (60x + 2000)-(20 x + 4000)
Now, simplify it:
Profit = 60x + 2000 -20x -4000
Profit = 40x – 2000
To earn some profit, 40x – 2000 > 0
⇒ 40x > 2000
⇒ x>2000/40
⇒ x > 50
Thus, the manufacturer should sell more than 50 items to realise some profit.
Q2: Ravi scored 70 and 75 marks in the first two-unit test. Calculate the minimum marks he should get in the third test to have an average of at least 60 marks.
Ans: Assume that x be the marks obtained by Ravi in the third unit test.
It is given that the student should have an average of at least 60 marks.
From the given information, we can write the linear inequality as:
(70+75+x)/3 ≥ 60
Now, simplify the expression:
⇒ (145 +x) ≥ 180
⇒ x ≥ 180 -145
⇒ x ≥ 35
Hence, the student should obtain a minimum of 35 marks to have an average of at least 60 marks.
Q3: Solve 3x + 8>2, when
(i) x is an integer
(ii) x is a real number
Ans: Given Linear inequality: 3x+8>2
The given inequality can also be written as:
3x+8 -8 > 2 -8 …(1)
In the above inequality, -8 is multiplied on both the sides, as it does not change the definition of the given expression.
Now, simplify the expression (1)
⇒ 3x > -6
Now, both the sides, divide it by 3
⇒ 3x/3 > -6/3
⇒ x > -2
(i) x is an integer
Hence, the integers greater than -2 are -1,0,1,2,…etc
Thus, when x is an integer, the solutions of the given inequality are -1,0,1,2,…
Hence, the solution set for the given linear inequality is {-1,0,1,2,…}
(ii) x is a real number
If x is a real number, the solutions of the given inequality are all the real numbers, which
are greater than 2.
Therefore, in the case of x is a real number, the solution set is (-2, ∞)
Q4: Solve the given linear inequalities 3x-2 < 2x+1 and show the graph of the solution in the number line.
Ans: Given linear inequality: 3x-2 < 2x+1
Bring the x terms on one side and constant terms on another side
⇒ 3x-2x < 1+2
⇒ x < 3
Therefore, the graphical representation for the solution of a linear inequality in number line is as follows: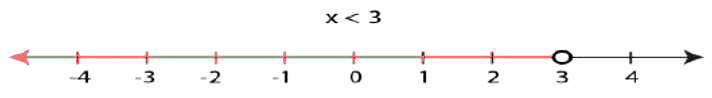
|
80 videos|315 docs|99 tests
|





















