Important Questions: Sets | Mathematics (Maths) Class 11 - Commerce PDF Download
Q1: Write the following sets in roster form:
(i) A = {x : x is an integer and –3 ≤ x < 7}
Ans: A = {x : x is an integer and –3 ≤ x < 7}
Integers are …-5, -4, -3, -2, -2, 0, 1, 2, 3, 4, 5, 6, 7, 8,…..
A = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
(ii) B = {x : x is a natural number less than 6}
Ans: B = {x : x is a natural number less than 6}
Natural numbers are 1, 2, 3, 4, 5, 6, 7, ……
B = {1, 2, 3, 4, 5}
Q2: Let X = {1, 2, 3, 4, 5, 6}. If n represent any member of X, express the following as sets:
(i) n ∈ X but 2n ∉ X
Ans: For X = {1, 2, 3, 4, 5, 6}, it is given that n ∈ X, but 2n ∉ X.
Let, A = {x | x ∈ X and 2x ∉ X}
Now, 1 ∉ A as 2.1 = 2 ∈ X
2 ∉ A as 2.2 = 4 ∈ X
3 ∉ A as 2.3 = 6 ∈ X
But 4 ∈ A as 2.4 = 8 ∉ X
5 ∈ A as 2.5 = 10 ∉ X
6 ∈ A as 2.6 = 12 ∉ X
Therefore, A = {4, 5, 6}
(ii) n + 5 = 8
Ans: Let B = {x | x ∈ X and x + 5 = 8}
Here, B = {3} as x = 3 ∈ X and 3 + 5 = 8 and there is no other element belonging to X such that x + 5 = 8.
(iii) n is greater than 4
Ans: Let C = {x | x ∈ X, x > 4}
Therefore, C = {5, 6}
Q3: Use the properties of sets to prove that for all the sets A and B, A – (A ∩ B) = A – B
Ans: A – (A ∩ B) = A ∩ (A ∩ B)′ (since A – B = A ∩ B′)
= A ∩ (A′ ∪ B′) [by De Morgan’s law)
= (A∩A′) ∪ (A∩ B′) [by distributive law]
= φ ∪ (A ∩ B′)
= A ∩ B′ = A – B
Hence, proved that A – (A ∩ B) = A – B.
Q4: In a class of 60 students, 23 play hockey, 15 play basketball,20 play cricket and 7 play hockey and basketball, 5 play cricket and basketball, 4 play hockey and cricket, 15 do not play any of the three games. Find
(i) How many play hockey, basketball and cricket
(ii) How many play hockey but not cricket
(iii) How many play hockey and cricket but not basketball
Ans: The Venn diagram of the given data is:
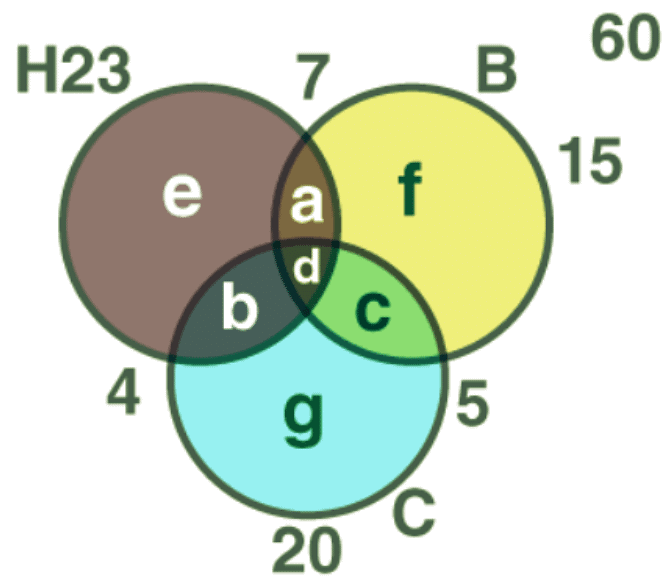
15 students do not play any of three games.
n(H ∪ B ∪ C) = 60 – 15 = 45
n(H ∪ B ∪ C) = n(H) + n(B) + n(C) – n(H ∩ B) – n(B ∩ C) – n(C ∩ H) + n(H ∩ B ∩ C)
45 = 23 + 15 + 20 – 7 – 5 – 4 + d
45 = 42 + d
d = 45- 42 = 3
Number of students who play all the three games = 3
Therefore, the number of students who play hockey, basketball and cricket = 3
a + d = 7
a = 7 – 3 = 4
b + d = 4
b = 4 – 3 = 1
a + b + d + e = 23
4 + 1 + 3 + e = 23
e = 15
Similarly, c = 2, g =14, f = 6
Number of students who play hockey but not cricket = a + e
= 4 + 15
= 19
Number of students who play hockey and cricket but not basketball = b = 1
Q5: In a survey of 600 students in a school, 150 students were found to be drinking Tea and 225 drinking Coffee, 100 were drinking both Tea and Coffee. Find how many students were drinking neither Tea nor Coffee.
Ans: Given,
Total number of students = 600
Number of students who were drinking Tea = n(T) = 150
Number of students who were drinking Coffee = n(C) = 225
Number of students who were drinking both Tea and Coffee = n(T ∩ C) = 100
n(T U C) = n(T) + n(C) – n(T ∩ C)
= 150 + 225 -100
= 375 – 100
= 275
Hence, the number of students who are drinking neither Tea nor Coffee = 600 – 275 = 325
Q6: Write the following sets in the roster form.
(i) A = {x | x is a positive integer less than 10 and 2x – 1 is an odd number}
Ans: 2x – 1 is always an odd number for all positive integral values of x since 2x is an even number.
In particular, 2x – 1 is an odd number for x = 1, 2, … , 9.
Therefore, A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
(ii) C = {x : x2 + 7x – 8 = 0, x ∈ R}
Ans: x2 + 7x – 8 = 0
(x + 8) (x – 1) = 0
x = – 8 or x = 1
Therefore, C = {– 8, 1}
Q7: Given that N = {1, 2, 3, …, 100}, then
(i) Write the subset A of N, whose elements are odd numbers.
Ans: A = {x | x ∈ N and x is odd}
A = {1, 3, 5, 7, …, 99}
(ii) Write the subset B of N, whose elements are represented by x + 2, where x ∈ N.
Ans: B = {y | y = x + 2, x ∈ N}
1 ∈ N, y = 1 + 2 = 3
2 ∈ N, y = 2 + 2 = 4, and so on.
Therefore, B = {3, 4, 5, 6, … , 100}
Q8: Let U = {1, 2, 3, 4, 5, 6}, A = {2, 3} and B = {3, 4, 5}.
Find A′, B′, A′ ∩ B′, A ∪ B and hence show that ( A ∪ B )′ = A′∩ B′.
Ans: Given,
U = {1, 2, 3, 4, 5, 6}, A = {2, 3} and B = {3, 4, 5}
A′ = {1, 4, 5, 6}
B′ = { 1, 2, 6 }.
Hence, A′ ∩ B′ = { 1, 6 }
Also, A ∪ B = { 2, 3, 4, 5 }
(A ∪ B)′ = { 1, 6 }
Therefore, ( A ∪ B )′ = { 1, 6 } = A′ ∩ B′
Q9: Let U = {1, 2, 3, 4, 5, 6, 7}, A = {2, 4, 6}, B = {3, 5} and C = {1, 2, 4, 7}, find
(i) A′ ∪ (B ∩ C′)
(ii) (B – A) ∪ (A – C)
Ans: Given,
U = {1, 2, 3, 4, 5, 6, 7}, A = {2, 4, 6}, B = {3, 5} and C = {1, 2, 4, 7}
(i) A′ = {1, 3, 5, 7}
C′ = {3, 5, 6}
B ∩ C′ = {3, 5}
A′ ∪ (B ∩ C′) = {1, 3, 5, 7}
(ii) B – A = {3, 5}
A – C = {6}
(B – A) ∪ (A – C) = {3, 5, 6}
Q10: Let U = {x : x ∈ N, x ≤ 9}; A = {x : x is an even number, 0 < x < 10}; B = {2, 3, 5, 7}. Write the set (A U B)’.
Ans: Let U = {x : x ∈ N, x ≤ 9}; A = {x : x is an even number, 0 < x < 10}; B = {2, 3, 5, 7}
U = { 1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {2, 4, 6, 8}
A U B = {2, 3, 4, 5, 6, 7, 8}
(A U B)’ = {1, 9}
|
75 videos|238 docs|91 tests
|
FAQs on Important Questions: Sets - Mathematics (Maths) Class 11 - Commerce
| 1. What is a set in mathematics? |  |
| 2. How are sets typically represented in mathematics? |  |
| 3. What is the cardinality of a set? |  |
| 4. What is the difference between a subset and a proper subset? |  |
| 5. How are sets related to mathematical operations like union and intersection? |  |

|
Explore Courses for Commerce exam
|

|

















