Inequalities - Examples (with Solutions), Miscellaneous, Quantitative Reasoning | Reasoning Aptitude for Competitive Examinations - Bank Exams PDF Download
Introduction
Inequality Reasoning refer to expressions that contain inequality signs such as <, >, =, etc. To understand the questions based on mathematical inequalities, candidates must know about various signs, which are used in such types of questions. There are also various types of inequalities, which are discussed in this article.
Questions of Inequality Reasoning are usually easy in nature. In this article, we are going to cover the key Inequality Logical Reasoning concepts with the solved examples, practice questions, tips, and inequality reasoning tricks, and other important details.
What is Inequality?
As mentioned above, Inequality refers to expressions that contain inequality signs such as <, >, =, etc. To understand the questions based on mathematical inequalities, candidates must know about various signs, which are used in such types of questions.
The same is given below:
Types of Inequalities
As now we know what consists of the questions related to the Inequality reasoning section. Let us see the various types of questions that may come one by one from below:1. Basic Inequality
In these type of Inequality reasoning questions, expressions consisting of comparison between different elements will be given and a defined relation between any 2 elements will be asked.
2. Either – or Case
In these type of Inequality reasoning questions, a definite relation between two elements cannot be determined. In this type of question there will be given 2 relations only from which either relation 1 or 2 can be true.
3. Coded Inequality
In these type of Inequality reasoning questions, codes will be assigned to inequality symbols and the expression will be given using those codes. Candidates need to decode the symbols and find the relation between the elements.
For Example,
Read the statements and check which conclusion is true.
Coded Inequality Question- 1:
In the given statements, the relations are represented as follows:
‘P # Q‘ means ‘P is not smaller than Q’.
‘P $ Q‘ means ‘P is neither smaller than nor equal to Q’.
‘P % Q‘ means ‘P is neither greater than nor smaller than Q’.
‘P ^ Q’ means ‘P is not greater than Q’.
‘P & Q’ means ‘P is neither greater than nor equal to Q’.
Statements:
1. X # Y
2. Y $ Z
3. A & Z
Conclusions:
1. Z & X
2. A $ Y
Options:
(a) Only conclusion I holds true.
(b) Only conclusion II holds true.
(c) Either conclusion I or II holds true.
(d) Neither conclusion I nor II holds true.
(e) Both conclusions I and II hold true.
Sol:
Option (a)
At first, the code must be interpreted in the general form. Here the symbols can be interpreted as :
# means ≥
$ means > and
& means <
Representing the statements in general form gives:
- X ≥ Y
- Y > Z
- A < Z
Similarly, the conclusions can be interpreted as, Z < X and A > Y.
Thus, from the given conclusions, Z < X holds true. But as A < Z and Z < Y, the conclusion A > Y is false. So, only the first conclusion follows.
Tips and Tricks to approach Inequality Questions
 The questions related to inequalities are mainly of two types i.e.
The questions related to inequalities are mainly of two types i.e.
- Direct Inequalities
- Indirect Inequalities
The detailed explanations for both these types are given below along with several solved examples to help the CAT aspirants understand the topic in a better way.
Basic Rules to Solve Inequalities
- A relation can be defined only if the statements of inequalities have a common term.
For example, if A > B and B>C, it can be concluded that A > C. - A relation is considered undefined if the inequalities do not have a common term.
For example, if A > B and C > D, the relation between A and D is undefined. - In case of complementary pairs, only the complementary relation is defined.
For example, if A ≥ B and B ≥ C, the relation between A and C can only be A ≥ C and not A > C.
Direct Inequalities
- The questions related to direct inequalities only includes basic symbols of inequalities like <, >, =, ≥, etc.
- In these questions, the candidates are given a set of sentences followed by a set of conclusions. The candidates are required to analyze the conclusion and answer the question accordingly.
Examples of Direct Inequality Reasoning Questions :
Read the statements and check which conclusion is true.
Direct Inequality Question- 1:
Statements:
1. A > B = C
2. G < C > D
Conclusions:
1. A < D
2. A = G
Options:
(a) Only conclusion I holds true.
(b) Only conclusion II holds true.
(c) Either conclusion I or II holds true.
(d) Neither conclusion I nor II holds true.
(e) Both conclusions I and II hold true.
Sol:Option (d)
From the given statements, it can be concluded that A must be greater than D as D < C < A.
Also, as C > G, A can never be equal to G.
Direct Inequality Question- 2:
Statement:
1. I ≥ U > T ≤ R
2. U ≥ V = W > C
Conclusions:*
1.W > T
2. C > I
Options:
(a) Only conclusion I holds true.
(b) Only conclusion II holds true.
(c) Either conclusion I or II holds true.
(d) Neither conclusion I nor II holds true.
(e) Both conclusions I and II hold true.
Sol:
Option (d)
Conclusion 1 does not holds true as T < U while U ≥ W. Similarly, conclusion 2 also does not hold since I ≥ U and U ≥ C.
Solving Inequation
On the basis of the laws of inequality, we have the following working rules.
1. Rule of Addition and Subtraction: Adding or subtracting a fixed number to each side of an inequality
produces an equivalent inequality.
Example: Adding 2 to each side of the inequality x – 2 ≤ 1 is equivalent to x ≤ 3.
2. Rule of multiplication/division by a positive number: All terms on both sides of an inequality can be
multiplied or divided by a positive number.
3. Rule of multiplication/division by a negative number: If all terms on both sides of an inequality are
multiplied or divided by a negative number, the sign of the inequality will be reversed.
Example: If 6x – 4 < – 8x + 6 then or – 3x + 2 > 4x – 3
Using the above facts we take the following steps to solve linear inequation:
ax + b > cx + d.
Step 1: Make all terms containing the variable (unknown) x positive and on one side of the inequation,
and the constants on the other side by using rule 1.
Step 2: Put the inequation in the form px > q or px < q
Step 3: Divide both sides by positive p, using rule 3.
Inequalities
Graphing Solutions of Inequalities
Representation of the real number set R and its subsets:
The solution of a linear inequation in one variable consists of many real numbers but may not all real
numbers. As such the set of solutions is always a subset of real numbers.
Emphasize the fact that solving an inequality means describing a set not just finding a number. This set is the
solution set of the problem. To visualize the solution set, draw it on the number line. To do this, draw the
number line and shade the part of the number line corresponding to the solution set. The solution set to a
single inequality will be a half line that may or may not include the endpoint. When the endpoint is included,
draw a solid dot for the endpoint. When the endpoint is not included, draw a circle.
Ex.1 Represent the solution set of x ≤ 5 on a number line.
Sol. The solution set of x ≤ 5 is represented by the set of point to the left of 5 on the number line. It does
include the endpoint, since x = 5 is included.
Solution Sets
The solution of any inequation is always expressed in a solution set. These solution the basis of requirement
of the elements contained in them can be classified as below:
a. Ranges where the ends are excluded: If the value of x is denoted as (1, 2) it means 1 < x < 2 i.e. x is
greater than 1 but smaller than 2.
b. Ranges where the ends are included
[2, 5] means 2 ≤ x ≤ 5
c. Mixed Ranges
(3, 21] means 3 < x ≤ 21
d. If solution set = {1, 2} means x = 1 and 2 only.
Ex.2 Solve for x, – 2x > 4
Sol. – 2x > 4
Divide both sides by – 2,
Graphically, the solution is:
Some more examples:
Ex.3 P is the solution set of and R is the solution set of : 5
. Where x ∈ W, find
the set P ∩ R.
Sol. For finding the solution set of P solve the inequation.
i.e. x < 1.33, but x ∈ W.
So solution set of P = {1} since for x = 0 the inequation is not defined
Now for solution set of R when x ≠ 0.
Solving we have, x ≤ 1 but x ≠ 0. Hence solution set R =- {0,1}
P ∩ R = {0,1}.
Properties of inequalities
(i) If a > b and b > c, then a > c.
(ii) If a > b and c is any real number, then a + c > b + c and a – c > b – c.
(iii) If a1 > b1, a2, > b1, ….an > bn, then a1 + a2 +…….an > b1 + b2 + ….bn.
(iv) If a1 > b1, a2 > b2, ……..an > bn and the a’s and the b’s are all positive real numbers. Then a1 . a2….an >
b1 . b2….bn.
(v) If a > b > 0, then
(vi) If a > b > 0 and n is a positive integer,
then an > bn, a–n < b-n and a1/n > b1/n provided in the last inequality only real
positive values of the nth roots are taken into account.
| Do you know? If a1 > b1 and a2 > b2, then it does not necessarily follow that a1 - a2 > b1 - b2 |
(vii) If x > y > 0, then loga x > loga y if a > 1and loga x < loga y if 0 < a < 1.
(viii) If x > y > 0, then ax > ay if a > 1, and ax < ay if 0 < a < 1.
(ix) If a > b > 0 and x > 0, then ax > bx.
(x) The Arithmetic mean of n positive numbers is always greater than their Geometric means.
i.e. if a1, a2. …. an are all positive then
(xi) If the sum of n positive numbers is a constant, then their product is
maximum when they are all equal; if their product is a constant their sum is
minimum when they are equal.
i.e. If a1 + a2 + …..+ an = constant k, where a’s are all positive, then a1 .
a2…an is maximum when
Also, if ,= constant k where the a’s are all positive, then
is Minimum
when
CHALLENGER
list one of the solution set of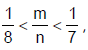
where m, n ∈ Z
(xii) a2 + b2 + c2 > ab + be + ca
(xiii) (n!)2 > nn , for all n > 2
(xiv)
(xv) a2b + b2c + c2a > 3abc
(xvi)
(xvii)
Ex.4 What values for X satisfy the inequality x2 – 10x + 21 <0
(1) x < 3
(2) x > 7
(3) 3 < x < 7
(4) No solution.
Sol. x2 −10x + 21< 0 means (x – 3) (x – 7) < 0. So x – 3 < 0 and x – 7 > 0 or x – 3 > 0 and
x – 7 < 0. By drawing on the number line, the intersecting part will be 3 < x < 7.
Answer: (3)
(or)
Go with the options.
It is very simple to solve the inequality questions from the options.
Take option (1), since it is x<3, take any value for x, which is less than 3. If the inequality does not
satisfy, then we can eliminate this option. Some times two options satisfy the inequality. Then we have
to pick the option which has maximum range.
Here x = 2 does not satisfy the inequality, hence option (1) is eliminated.
Similarly x = 8 does not satisfy. So option (2) also can be eliminated.
Since the inequality is satisfied for x = 4, 5,… Option (3) is the required answer.
Ex.5 If x3 – 3x2 – 6 x + 8 > 0; then X can be best described by,
(1) x < 4
(2) – 2 < x < 1
(3) x > 4
(4) both (2) and (3)
Sol. It is better to solve this with the help of options
x = 3 does not satisfy the inequality, so option (1) is eliminated.
The inequality is satisfied by all the values of option (2) and the values of option (3) also satisfy this. So
the required. Answer: (4)
Solutions of Quadratic Inequalities
Solving linear inequalities, such as "x + 3 > 0", was pretty straightforward, as long as you remembered to flip
the inequality sign whenever you multiplied or divided throughout by a negative number (as you would when
solving something like "– 2x < 4").
We can follow the same method of finding intercepts and using graphs to solve inequalities containing
quadratics. When we have an inequality with "x2" as the highest-degree term, it is called a "quadratic
inequality".
Let us consider a quadratic equation having two roots a and b, such that a > b. then
(i) (x – a) (x – b) > 0
(ii) (x – a) (x – b) < 0 are the possible inequalities.
If we plot the graph of the quadratic equation with roots a and b, we get
So from the graph the solution of the above two equations are
(i) Either x < b or x > a
(ii) But on the other end the value b < x < a is the solution of equation 2.
Ex.6 – x2 + 4 < 0.
Sol. – x2 + 4 < 0.
4 – x2 < 0.
(2 – x) (2 + x) < 0.
CASE 1.
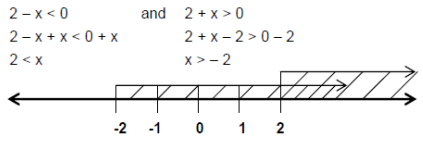
From the number line we have
x > 2 ……..(1)
CASE 2.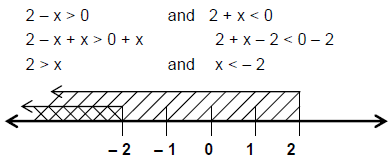 Image caption
Image caption
So the solution set x < – 2
Solution Set = {x > 2 or x < – 2}
Higher Degree Inequations
The polynomial inequations of degree 3 or more are polynomials of higher degree. Let us consider an
inequation of degree 3.
(x + 1) (x – 2) (x – 4) > 0 ………….. (1)
Well this is the inequation of as the multiplication of three numbers whose result should be positive i.e. p x q x
r > 0 where p, q & r are real numbers. The product of three real numbers should be positive if all of them are
positive or at least two of them positive.
In the given equation we have three points where the inequation change its nature. These points are x = (– 1,
2, 4). The nature of inequation can be explained below in the table –
Value of x | (x + 1) | (x - 2) | (x - 4) | (x + 1) (x - 2) (x - 4) |
x < -1 | - ve | -ve | -ve | (x+ 1)(x -2 )(x-4)< 0 |
-1< x < 2 | + ve | -ve | -ve | (x + 1)(x - 2) (x - 4)>0 |
2< x < 4 | + ve | + ve | -ve | (x + 1) (x - 2) (x - 4) < 0 |
x > 4 | + ve | + ve | + ve | (x + 1) (x - 2) (x - 4) > 0 |
So from the table we have the solution set of the inequation.
Solution Set = – 1 < x < 2 or x > 4
If we wish to solve the above inequation by graphical method then the graph will be as follows
Ex.7 Solve the inequation graphically and give the general solution of both the equations.
i. (X – a) (X – b) (X – c) (X – d) > 0
ii. (X – a) (X – b) (X – c) (X – d) < 0,
Where a, b, c & d are real numbers and a < b < c < d
Absolute value
The absolute value |x|, read as the modulus of x of a real number x is defined as
|x| = x if x ≥ 0 and |x| = – x, if x < 0.
Thus |x| ≥ 0; |x| = |– x|
Modulus and inequality
General solution of the inequation containing modulus:
(a) If |x| = c ⇒ x = {– c, c}
(b) If |x| > c ⇒ x > c or x < – c
(c) If x < c ⇒ – c < x < c.
Ex.8 What is the solution set of equation x2 + 5|x| + 6 > 0 ?
Sol. Case 1: If x ≥ 0, then |x| = x
So we have, x2 + 5x + 6 > 0
⇒ (x + 2) (x + 3) > 0
When both positive we get, x > -2 but x ≥ 0
Hence solution set = {x | x ≥ 0 and x ∈ R} …………(1)
When both negatives then we have, x < – 3 but x is positive, So no solution.
Case 2: If x < 0, then |x| = -x
We have, x2 – 5x + 6 > 0
⇒ (x – 2) (x – 3) > 0
Solving the inequality we will have x > 3 or x < 2 but here x < 0
So solution set = {x | x < 0 & x ∈ R} ……………(2)
From equation 1 and 2 we have x ∈ R is the solution of the given equation.
| Toolkit (i) |x - a| = x - a if x > a and |x - a| = a - x, if x < a (ii) If b > 0, then |x - a|<b ⇒ -b < x - a < b or a - b < x < a + b (iii) |x - a|>b ⇒ x - a > b or a - x > b ⇒ x > a + b or x < a - b (iv) |x - a| = b ⇒ x - a = b or a - x = b ⇒ x = a + b or x = a - b (v) |a + b| < |a| + |b|, i.e (sum) < sum of moduli (vi) |a - b| > |a| - |b| (vii) |a b| = |a| |b|, mod (product) = product of moduli |
Ex.9 Solve |2x + 3| < 6.
Sol. Since this is a "less than" absolute value inequality, the first step is to clear the absolute value
according to the pattern:
|2x + 3| < 6
– 6 < 2x + 3 < 6 [this is the pattern for "less than"]
– 6 – 3 < 2x + 3 – 3 < 6 – 3
– 9 < 2x < 3 < x <
Then the solution to |2x + 3| < 6 is the interval < x <
Best approach to solve the inequality questions is to approach the questions by options.
Ex.10 Solution of the inequality: |x + 2| > |3x – 5| is
(1)
(2)
(3)
(4)
(5)
Sol. Pick any option & check any value of x satisfying the inequality.
Let us take x = 2 which lies in option (1) & (2) & (5), If x = 2 satisfies the given equation then one out of
(1) or (2) or (5) is the answer otherwise one out of (3) or (4) is the answer.
Put x = 2 in |x + 2| > |3x – 5| we get
4 > 1 which is true so choice (3) & (4) can be eliminated
Put x = 1 we get
3 > 2 which is true and hence (1) is eliminated, because it doesn’t has x = 1.
Now take x = – 1, we get 1 > 8, which is wrong, so option (5) is eliminated.
So answer is (2).
|
73 videos|86 docs|121 tests
|
FAQs on Inequalities - Examples (with Solutions), Miscellaneous, Quantitative Reasoning - Reasoning Aptitude for Competitive Examinations - Bank Exams
| 1. What is the definition of an inequality? |  |
| 2. How do you solve an inequality? |  |
| 3. What are the different types of inequalities? |  |
| 4. How can inequalities be represented graphically? |  |
| 5. Can you provide an example of solving an inequality? |  |






















