Coded inequalities -1 | Quantitative Aptitude (Quant) - CAT PDF Download
Question 1: How many positive integer values can x take that satisfy the inequality (x - 8) (x - 10) (x - 12).......(x - 100) < 0?
A. 25
B. 30
C. 35
D. 40
Answer. 30
Explanation.
Let us try out a few values to see if that gives us anything.
When x = 8, 10, 12, ....100 this goes to zero. So, these cannot be counted.
When x = 101, 102 or beyond, all the terms are positive, so the product will be positive.
So, straight-away we are down to numbers 1, 2, 3, ...7 and then odd numbers from there to 99.
Let us substitute x = 1,
All the individual terms are negative. There are totally 47 terms in this list (How? Figure that out). Product of 47 negative terms will be negative.
So, x = 1 works. So, will x =2, 3, 4, 5, 6, and 7.
Remember, product of an odd number of negative terms is negative; product of even number of negative terms is positive. Now, this idea sets up the rest of the question.
When x = 9, there is one positive terms and 46 negative terms. So, the product will be positive.
When x = 11, there are two positive terms and 45 negative terms. So, the product will be negative.
When x = 13, there are three positive terms and 44 negative terms. So, the product will be positive.
and so on.
Essentially, alternate odd numbers need to be counted, starting from 11.
So, the numbers that will work for this inequality are 1, 2, 3, 4, 5, 6, 7...and then 11, 15, 19, 23, 27, 31,..... and so on.
What will be the last term on this list?
99, because when x = 99, there are 46 positive terms and 1 negative term.
So, we need to figure out how many terms are there in the list 11, 15, 19,....99. These can be written as
4 * 2 + 3
4 * 3 + 3
4 * 4 + 3
4 * 5 + 3
4 * 6 + 3
...
4 * 24 + 3
A set of 23 terms. So, total number of values = 23 + 7 = 30. 30 positive integer values of x exist satisfying the condition.
The question is "How many positive integer values can x take that satisfy the inequality (x - 8) (x - 10) (x - 12).......(x - 100) < 0?"
Hence the answer is "30"
Choice B is the correct answer.
Question 2: Solve the inequality x3 – 5x2 + 8x – 4 > 0.
A. (2, ∞)
B. (1, 2) ∪ (2, ∞)
C. (-∞, 1) ∪ (2, ∞)
D. (-∞, 1)
Answer. (1, 2) ∪ (2, ∞)
Explanation.
Let a, b, c be the roots of this cubic equation
a + b + c = 5
ab + bc + ca = 8
abc = 4
This happens when a = 1, b = 2 and c = 2 {This is another approach to solving cubic equations}.
The other approach is to use polynomial remainder theorem
If you notice, sum of the coefficients = 0
⇒ P(1) = 0
⇒ (x - 1) is a factor of the equation. Once we find one factor, we can find the other two by dividing the polynomial by (x - 1) and then factorizing the resulting quadratic equation.
(x - 1) (x - 2) (x - 2) > 0
Let us call the product (x - 1) (x - 2) (x - 2) as a black box.
If x is less than 1, the black box is a –ve number
If x is between 1 and 2, the black box is a +ve number
If x is greater than 2, the black box is a +ve number
Since we are searching for the regions where the black box is a +ve number, the solution is as follows: 1 < x < 2 OR x > 2
The question is "Solve the inequality x3 – 5x2 + 8x – 4 > 0."
Hence the answer is "(1, 2) ∪ (2, ∞)"
Choice B is the correct answer.
Question 3: Find the range of x for which (x + 2) (x + 5) > 40?
Answer. x < -10 or x > 3
Explanation.
There are two ways of trying this one. We can expand and simplify this algebraically.
x2 + 7x + 10 > 40 or x2 + 7x - 30 > 0
(x + 10) (x - 3) > 0
The roots are -10 and +3.
⇒ x should lie outside the roots.
Now, what is this based on?
There is a simple thumb rule for solving quadratic inequality
For any quadratic inequality ax2 + bx + c < 0
Factorize it as a(x - p) (x - q) < 0
Whenever a is greater than 0, the above inequality will hold good if x lies between p and q.
a(x - p) (x - q) will be greater than 0, whenever x does not lie between p and q. In other words x should lie in the range (-∞, p) or (q, ∞).
Now, coming back to the question (x + 10) (x - 3) > 0 Or, x < -10 or x > 3
Second method:
5 * 8 = 40, -8 * -5 = 40
So, if x + 2 > 5 this will hold good ⇒ x > 3
If x + 2 is less than -8 also, this will hold good ⇒ x < -10.
The first method is far more robust.
The question is "Find the range of x for which (x + 2) (x + 5) > 40?"
Hence the answer is "x < -10 or x > 3"
Question 4: How many integer values of x satisfy the inequality x( x + 2)(x + 4)(x + 6) < 200?
Explanation.
To begin with - 0, -2, -4 and -6 work. These are the values for which the left-hand side goes to zero.
There are 4 terms in the product. If all 4 are positive or all 4 are negative the product will be positive.
The product can be negative only if exactly 1 or exactly 3 are negative. When 1 or 3 terms are negative, the product is clearly less than 200.
When x = -1, one term is negative
When x = -5, three terms are negative
So, adding these two numbers also to the set of solutions {-6, -5, -4, -2, -1, 0} satisfy the inequality.
Beyond this it is just trial and error.
Let us try x = 1. Product is 1 * 3 * 5 * 7 = 105. This works
x = -7 gives the same product. So, that also works.
So, the solution set is now refined to {-7, -6, -5, -4, -2, -1, 0, 1}
x = 2 ⇒ Product is 2 * 4 * 6 * 8 = 8 * 48. Not possible. Any x greater than 1 does not work.
x = -8 is also not possible. Any value of x less than -7 does not work.
So, the solution set stays as {-7, -6, -5, -4, -2, -1, 0, 1}
The one missing value in this sequence is -3. When x = -3, product becomes -3 * -1 * 1 * 3. = 9. This also holds good.
So, values {-7, -6,-5, -4, -3, -2, -1, 0, 1} hold good. 9 different values satisfy this inequality.
The question is "How many integer values of x satisfy the inequality x(x + 2)(x + 4)(x + 6) < 200?"
Hence the answer is "There are a total of nine values "
Question 5: Find the range of x where ||x - 3| - 4| > 3?
Answer. (-∞, -4) or (2, 4) or ( 10, ∞)
Explanation.
If we have an inequality |y| > 3, this will be satisfied if => y > 3 or y < -3.
So, the above inequality simplifies to two inequalities
Inequality I: |x - 3| - 4 > 3
|x - 3| - 4 > 3 => |x - 3| > 7
x - 3 > 7 or x - 3 < -7
Or, x > 10 or x < -4
Of, x lies outside of -4 and 10. Or, x can lie in the range (-∞, -4) or ( 10, ∞)
Inequality II: |x - 3| - 4 < -3
|x - 3| - 4 < - 3
⇒ |x - 3| < 1
⇒ -1 < x - 3 < 1 or x lies between 2 and 4
So, final solution is given by the range
(-∞, -4) or (2, 4) or (10, ∞)
The question is "Find the range of x where ||x - 3| - 4| > 3?"
Hence the answer is "(-∞, -4) or (2, 4) or ( 10, ∞)"
Question 6: The sum of three distinct natural numbers is 25. What is the maximum value of their product?
Answer. 560
Explanation.
Let the three natural numbers be a, b and c. We know that a + b + c = 25.
Let us substitute some values and see where this is headed
a = 1, b = 2 c = 22, Product = 44
a = 2, b = 3 c = 20, product = 120
a = 5, b = 6 c = 14, product = 420
The numbers should be as close to each other as possible. (Just trial and error and one can figure this out). This property is an extension of the AM-GM Inequality.
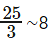
25 divided by 3 is approximately equal to 8. So, we should choose a, b, and c close enough to 8.
8 + 8 + 9 = 25. But the numbers need to be distinct. 8 * 7 * 10 come closest. The maximum product would be 560.
The question is "The sum of three distinct natural numbers is 25. What is the maximum value of their product?"
Hence the answer is "The maximum product is 560."
Question 7: If x (x + 3) (x + 5) (x + 8) < 250, how many integer values can x take?
Answer. x can take integer 11 values
Explanation.
Straight away we can see that x = 0 works. The product goes to zero in this case. When x takes values -3, -5 or -8, the product will go to zero and the inequality holds good.
Now, let us substitute some other values.
When x = 1 ⇒ Product = 1 * 4 * 6 * 9 = 216 < 250 So, x=1 holds good.
When x = 2 ⇒ The product is clearly greater than 250.
So, thus far, we have seen that for x = 0, -3, -5, -8 or 1; the above inequality holds good.
There are 4 terms in this product. If all 4 are positive or all 4 are negative, the product will be positive. If exactly one term is positive or exactly one term is negative, the product will be negative.
Whenever the product is negative, the inequality will hold good. So, let us find the values of x for which the product will be negative.
x = -1 or -2, the product is negative, so the inequality will hold good.
Let us think of other values of x for which the product is negative. For the product to be negative, either 1 or 3 of the four terms should be negative.
When x is -6 or -7, three of the terms are negative and the product is negative.
So, for x = 0, 1, -3, -5, -8, -1, -2, -6 or -7 this holds good. We have seen 9 values thus far.
In ascending order, the values are -8, -7, -6, -5, -3, -2, -1, 0, 1
The value in between that we have thus far not verified is -4. Let us try -4 as well.
In this case the product is -4 * -1 * 1 * 7 < 250
For x = -9, product is -9 * -6 * -4 * 1 = 216 < 250
Clearly for x = -10 or lesser the inequality does not hold good.
So, the inequality holds good for 11 terms. x can take all integers from -9 to +1 (both inclusive).
The question is "If x (x + 3) (x + 5) (x + 8) < 250, how many integer values can x take?"
Hence the answer is "x can take integer 11 values"
Question 8: (|x| - 2) (x + 5) < 0. What is the range of values x can take?
Answer. The range is (-∞, -5) or (-2, 2)
Explanation.
This can be true in two scenarios.
Scenario I: (|x| - 2) < 0 and (x + 5) > 0
Or |x| < 2 and x > -5.This gives us the range (-2, 2)
Scenario II: (|x| - 2) > 0 and (x + 5) < 0
Or |x| > 2 and x < -5. This gives us the range (-∞, -5)
So, the overall range is (-∞, -5) or (-2, 2)
The question is "(|x| - 2) (x + 5) < 0. What is the range of values x can take?"
Hence the answer is "The range is (-∞, -5) or (-2, 2)"
Question 9: a and b are roots of the equation x2 - px + 12 = 0. If the difference between the roots is at least 12, what is the range of values p can take?
Answer. (-∞, -2) or (-2, 2)
Explanation.
The roots are a and b:
a + b = p and
ab = 12
(a + b)2 = p2
(a - b)2 = (a + b)2 - 4ab
⇒ (a - b)2 = p2 - 12 * 4 = p2 - 48
If |a - b| ≥ 12 {Difference between the roots is at least 12}
then, (a - b)2 ≥ 144
p2 - 48 ≥ 144
p2 ≥ 192
P ≥ 8 √3 or P ≤ -8 √3
The question is "If the difference between the roots is at least 12, what is the range of values p can take?"
Hence the answer is "(-∞, -2) or (-2, 2)"
Question 10: If a, b, c are distinct positive integers, what is the highest value a * b * c can take if a + b + c = 31?
A. 1080
B. 1200
C. 1024
D. 1056
Answer. 1080
Explanation.
The sum of three numbers is given; the product will be maximum if the numbers are equal.

So, if a + b + c is defined, abc will be maximum when all three terms are equal. In this instance, however, with a, b, c being distinct integers, they cannot all be equal.
So, we need to look at a, b, c to be as close to each other as possible.
a = 10, b =10, c = 11 is one possibility, but a, b, c have to be distinct. So, this can be ruled out.
The close options are,
a, b, c: 9, 10, 12; product = 1080
a, b, c: 8, 11, 12; product = 1056
Maximum product = 1080
The question is "what is the highest value a * b * c can take if a + b + c = 31?"
Hence the answer is "1080"
Choice A is the correct answer.
Question 11: a, b, c are distinct natural numbers less than 25. What is the maximum possible value of |a – b| + |b – c| – |c – a|?
A. 44
B. 46
C. 23
D. 21
Answer. 44
Explanation.

For any two points M, N on the number line representing numbers m, n the distance MN = | m - n|.
So, for three points, P, Q and R on the number line |p – q|, |q – r|, |r – p| are distances between three pairs of points on the number line.
In this case, we are trying to find maximum value of |a – b| + |b – c| – |c – a|. If b lies between a and c, the above value would be zero. So, b should not be between a and c.
The best case scenario would be if a, c were very close to each other and far from b. Let us try b = 24, a = 1, c = 2.
In this case |a – b| + |b – c| – |c – a| = 23 + 22 – 1 = 44. This is the maximum possible value.
We could also have b = 1, a = 24, c = 23,
|a – b| + |b – c| – |c – a| = 23 + 22 – 1 = 44.
The question is "What is the maximum possible value of |a – b| + |b – c| – |c – a|?"
Hence the answer is "44"
Choice A is the correct answer.
Question 12: Consider integers p, q such that – 3 < p < 4, – 8 < q < 7, what is the maximum possible value of p2 + pq + q2?
A. 60
B. 67
C. 93
D. 84
Answer. 67
Explanation.
Trial and error is the best approach for this question. We just need to be scientific about this.
p2 and q2 are both positive and depend on |p| and |q|. If p, q are large negative or large positive numbers, p2 and q2 will be high.
pq will be positive if p, q have the same sign, and negative if they have opposite signs.
So, for p2 + pq + q2 to be maximum, best scenarios would be if both p & q are positive or both are negative.
Let us try two possibilities.
p = – 2, q = – 7: p2 + pq + q2 = 4 + 14 + 49 = 67
p = 3, q = 6: p2 + pq + q2 = 9 + 15 + 36 = 60
Whenever we have an expression with multiple terms, there are two key points to note.
The equation will be most sensitive to the highest power.
The equation will be more sensitive to the term with the greater value.
In the case, q.
In this question, we have a trade–off between higher value for p2 and q2. For q2, the choice is between 62 and (–7)2. This impact will overshadow the choice for p (where we are choosing between –2 and 3).
So, the maximum value for the expression would be 67.
The question is "what is the maximum possible value of p2 + pq + q2?"
Hence the answer is "67"
Choice B is the correct answer.
|
191 videos|131 docs|110 tests
|
FAQs on Coded inequalities -1 - Quantitative Aptitude (Quant) - CAT
| 1. How do you solve coded inequalities in exams? |  |
| 2. What are some common strategies for tackling coded inequalities questions? |  |
| 3. Can coded inequalities questions be time-consuming during exams? |  |
| 4. Are there any shortcuts or tricks for solving coded inequalities questions quickly? |  |
| 5. What should I do if I am unsure how to approach a coded inequalities question on an exam? |  |

|
Explore Courses for CAT exam
|

|


















