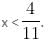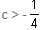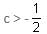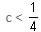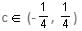This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Inequalities (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:How many pairs of integers satisfy the inequality |x| + |y| = 7?
Explanation
x = 0, y = ±7
Or x = ±1, y = ±6
Similarly, (±2, ±5)
(±3, ±4), (±4, ±3), (±5, ±2), (±6, ±1), (±7, 0)
(0, ±7) means (0, 7) or (0, -7) → 2 pairs
(±1, ±6) means (1, 6), (1, -6), (-1, 6), (-1, - 6) → 4 pairs
So, total number of possible pairs = 2 + 6 × 4 + 2 = 28
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:It is given that m and n are two real numbers. Which of the following is true for all possible values of m and n?
Explanation
(m - n)2 + (m - 1)2 + (n - 1)2 ≥ 0 [Any square is always non-negative]
⇒ m2 - 2mn + n2 + m2 - 2m + 1 + n2 - 2n + 1 ≥ 0
⇒ 2m2 + 2n2 + 2 ≥ 2mn + 2m + 2n
⇒ m2 + n2 + 1 ≥ mn + m + n {Dividing both sides by 2}
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:What is the sum of all possible values of m in the given inequality?
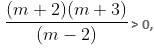 m is an integer, it is known that m ≤ 99.
m is an integer, it is known that m ≤ 99.
Explanation
m cannot be < -3 because that will result in (-ve)(-ve)/(-ve), which will be negative and thus < 0.
m cannot be -2 or -3 because that will result in 0, which is not > 0.
m cannot be -1, 0 or 1 because that will result in (+ve)(+ve)/(-ve), which is < 0.
m cannot be 2 because that will result in dividing by 0.
Thus, m can only be 3, 4, 5, 6, ......., 99.
So, required sum is
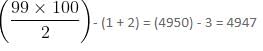
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:The number of solutions of the equation 2x + y = 40, where both x and y are positive integers and x ≤ y, is
Explanation
2x + y = 40
Possible pairs (x, y) are = (1, 38) (2, 36) ……….. (13, 14)
And (14, 12) is not possible because x ≤ y.
So, there are a total of 13 pairs.
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:If 2y - x > 2x - y, and 0 ≤ y ≤ 20, how many non-negative integer pairs of x and y satisfy the given inequalities?
Explanation
2y - x > 2x - y ⇒ y > x
i.e. y = 0, x < 0 ⇒ No pair exists.
y = 1, x = 0, ⇒ Number of pairs = 1
y = 2, x = 0, 1 ⇒ Number of pairs = 2
y = 3, x = 0, 1, 2 ⇒ Number of pairs = 3
…
…
…
If y = 20, x = 0 to 19 ⇒ Number of pairs
= 20
Total number of pairs = 1 + 2 + 3 + …… + 20 = 210
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:Consider the following system of inequalities:
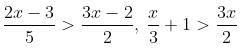
Which of the following options best describes the value of x?
Explanation
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:What is the least possible value of c - a if a < b < c and b - a > 5, where a is an even integer and b and c are odd integers?
Explanation
a is an even integer and b is an odd integer.
So, b - a will be odd.
Since b - a > 5 and c > b.
So, c - a will be minimum if c and b both are consecutive odd integers.
So, c - a > 7
Hence, minimum value of c - a will be 9 as c is odd and a is an even integer.
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:How many pairs of consecutive odd positive integers, smaller than 18 and having their sum as more than 20, are possible?
Explanation
Let x be the smaller of the two consecutive odd positive integers. Then, the other odd integer is x + 2.
It is given that both the integers are smaller than 18 and their sum is more than 20.
Therefore,
x + 2 < 18 and x + (x + 2) > 20
⇒ x < 16 and 2x + 2 > 20
⇒ x < 16 and 2x > 18
⇒ x < 16 and x > 9
⇒ 9 < x < 16
⇒ x = 11, 13, 15 [∵ x is an odd integer]
Hence, the required pairs of odd integers are (11, 13), (13, 15) and (15, 17).
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:If (1 + 3c), 1 and (1 - c) are the three sides of a triangle, then
Explanation
Report a problem
Question for Practice Questions Level 2: Inequalities - 2
Try yourself:If x satisfies the inequality |x − 1| + |x − 2| + |x − 3| ≥ 6, then:
Explanation
If we put x = 3,
Then |3 − 1| + |3 − 2|+|3 − 3| = 3 ≤ 6
Therefore option (a), (c), (d) are not correct.
Hence only option (b) is correct.
Report a problem
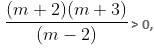 m is an integer, it is known that m ≤ 99.
m is an integer, it is known that m ≤ 99.
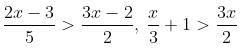

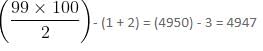

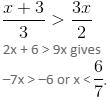
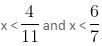 will be satisfied if
will be satisfied if