Insertion in AVL Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
AVL Tree
AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.
Example of AVL Tree
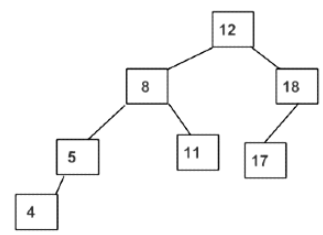
The above tree is AVL because the differences between the heights of left and right subtrees for every node are less than or equal to 1.
Example of a Tree that is NOT an AVL Tree
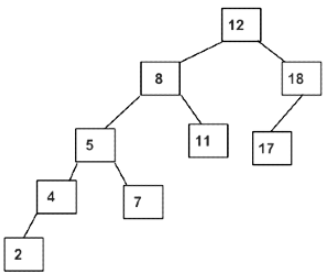
The above tree is not AVL because the differences between the heights of the left and right subtrees for 8 and 12 are greater than 1.
Why AVL Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that the height of the tree remains O(log(n)) after every insertion and deletion, then we can guarantee an upper bound of O(log(n)) for all these operations. The height of an AVL tree is always O(log(n)) where n is the number of nodes in the tree.
Insertion in AVL Tree
To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing.
Following are two basic operations that can be performed to balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
- Left Rotation
- Right Rotation
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side)
Keys in both of the above trees follow the following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Steps to follow for insertion:
Let the newly inserted node be w
- Perform standard BST insert for w.
- Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the child of z that comes on the path from w to z and x be the grandchild of z that comes on the path from w to z.
- Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that need to be handled as x, y and z can be arranged in 4 ways.
- Following are the possible 4 arrangements:
- y is the left child of z and x is the left child of y (Left Left Case)
- y is the left child of z and x is the right child of y (Left Right Case)
- y is the right child of z and x is the right child of y (Right Right Case)
- y is the right child of z and x is the left child of y (Right Left Case)
Following are the operations to be performed in above mentioned 4 cases. In all of the cases, we only need to re-balance the subtree rooted with z and the complete tree becomes balanced as the height of the subtree (After appropriate rotations) rooted with z becomes the same as it was before insertion.
1. Left Left Case
T1, T2, T3 and T4 are subtrees.
2. Left Right Case
 3. Right Right Case
3. Right Right Case

4. Right Left Case
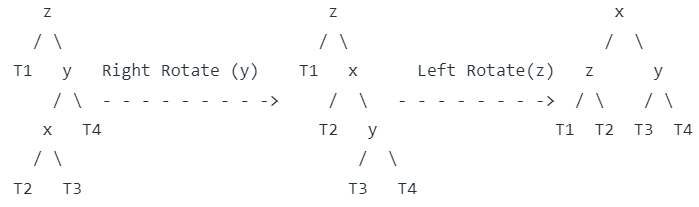
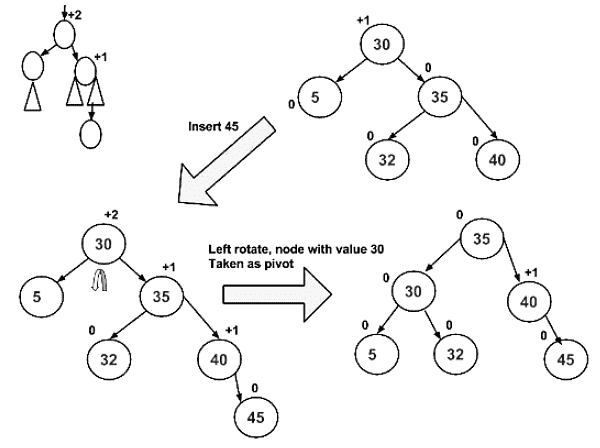
Illustration of Insertion at AVL Tree

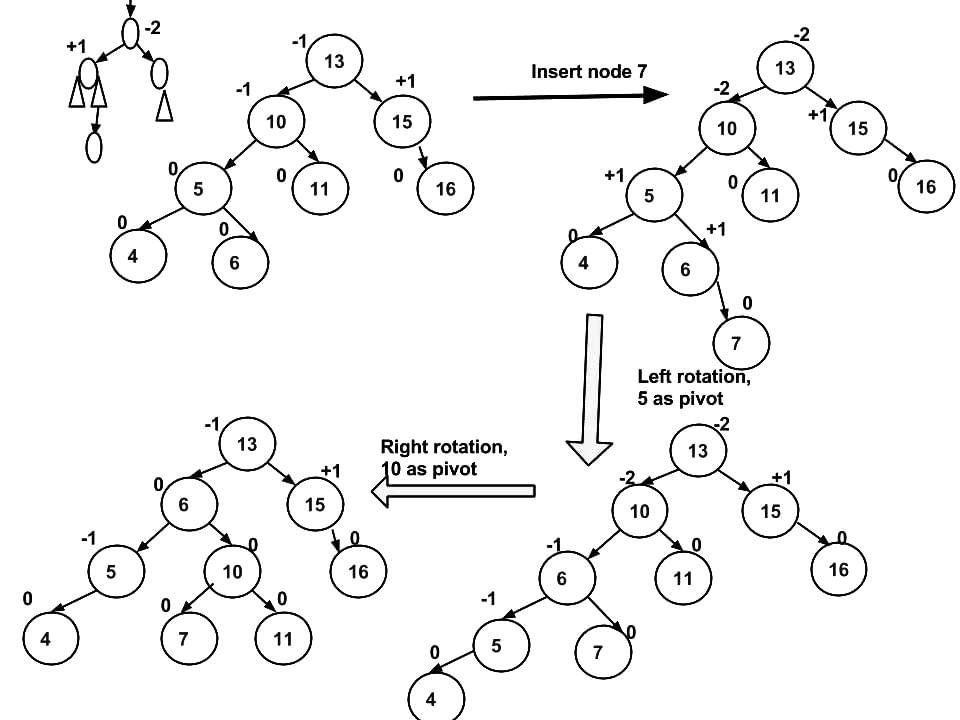
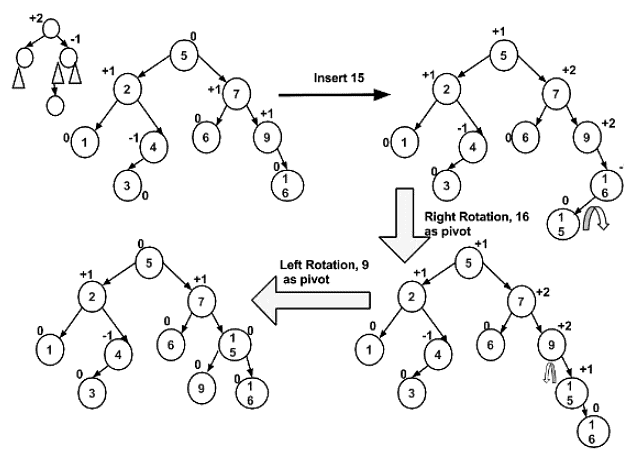
|
119 docs|30 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|

















