JEE Exam > JEE Notes > 35 Years Chapter wise Previous Year Solved Papers for JEE > Integer Answer Type Questions: Probability | JEE Advanced
Integer Answer Type Questions: Probability | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q.1. Of the three independent events E1, E2 and E3, the probability that only E1 occurs is α, only E2 occurs is β and only E3 occurs is γ. Let the probability p that none of events E1, E2 or E3 occurs satisfy the equations (α 2β)p = αβ and (β – 3γ)p = 2bg.
All the given probabilities are assumed to lie in the interval (0, 1). (JEE Adv. 2013)
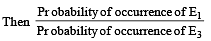
Ans. Sol. (6) Let P(E1) = x; P(E2) = y, P(E3) = z
P(only E1) = x(1 – y) (1 – z) = α
P(only E2) = (1 – x) y (1 – z) = β
P(only E3) = (1 – x) ( 1 – y) z = g
P(none) = (1 – x) (1 – y) (1 – z) = p.
Now given (α – 2β) p = αβ
⇒ x = 2y an d(β – 3r)p = 2βr ⇒ y = 3z
∴ x = 6z
Hence
Q.2. The minimum number of times a fair coin needs to be tossed, so that the probability of getting at least two heads is at least 0.96, is (JEE Adv. 2015)
Ans. Sol. P(x > 2) > 0.96
⇒ 1 – P(x = 0) – P(x = 1) > 0.96
⇒ P(x = 0) + P(x = 1) < 0.04
⇒ 
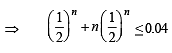
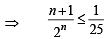⇒ minimum value of n is 8.
The document Integer Answer Type Questions: Probability | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE is a part of the JEE Course 35 Years Chapter wise Previous Year Solved Papers for JEE.
All you need of JEE at this link: JEE
|
347 docs|185 tests
|
Related Exams
About this Document
|
4.60/5 Rating |
|
Nov 23, 2024 Last updated |
Document Description: Integer Answer Type Questions: Probability | JEE Advanced for JEE 2024 is part of 35 Years Chapter wise Previous Year Solved Papers for JEE preparation.
The notes and questions for Integer Answer Type Questions: Probability | JEE Advanced have been prepared according to the JEE exam syllabus. Information about Integer Answer Type Questions: Probability | JEE Advanced covers topics
like and Integer Answer Type Questions: Probability | JEE Advanced Example, for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Integer Answer Type Questions: Probability | JEE Advanced.
Introduction of Integer Answer Type Questions: Probability | JEE Advanced in English is available as part of our 35 Years Chapter wise Previous Year Solved Papers for JEE
for JEE & Integer Answer Type Questions: Probability | JEE Advanced in Hindi for 35 Years Chapter wise Previous Year Solved Papers for JEE course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: Integer Answer Type Questions: Probability | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE
Description
Full syllabus notes, lecture & questions for Integer Answer Type Questions: Probability | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE - JEE | Plus excerises question with solution to help you revise complete syllabus for 35 Years Chapter wise Previous Year Solved Papers for JEE | Best notes, free PDF download
Information about Integer Answer Type Questions: Probability | JEE Advanced
In this doc you can find the meaning of Integer Answer Type Questions: Probability | JEE Advanced defined & explained in the simplest way possible. Besides explaining types of
Integer Answer Type Questions: Probability | JEE Advanced theory, EduRev gives you an ample number of questions to practice Integer Answer Type Questions: Probability | JEE Advanced tests, examples and also practice JEE
tests
|
347 docs|185 tests
|
Download as PDF
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Sample Paper
,past year papers
,Integer Answer Type Questions: Probability | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE
,ppt
,Exam
,Important questions
,Integer Answer Type Questions: Probability | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE
,Extra Questions
,Objective type Questions
,shortcuts and tricks
,Free
,video lectures
,mock tests for examination
,study material
,MCQs
,Viva Questions
,Previous Year Questions with Solutions
,Semester Notes
,Summary
,Integer Answer Type Questions: Probability | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE
,practice quizzes
;
Additional Information about Integer Answer Type Questions: Probability | JEE Advanced for JEE Preparation
Integer Answer Type Questions: Probability | JEE Advanced Free PDF Download
The Integer Answer Type Questions: Probability | JEE Advanced is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Integer Answer Type Questions: Probability | JEE Advanced now and kickstart your journey towards success in the JEE exam.
Importance of Integer Answer Type Questions: Probability | JEE Advanced
The importance of Integer Answer Type Questions: Probability | JEE Advanced cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Integer Answer Type Questions: Probability | JEE Advanced Notes
Integer Answer Type Questions: Probability | JEE Advanced Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Integer Answer Type Questions: Probability | JEE Advanced.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Integer Answer Type Questions: Probability | JEE Advanced Notes on EduRev are your ultimate resource for success.
Integer Answer Type Questions: Probability | JEE Advanced JEE
The "Integer Answer Type Questions: Probability | JEE Advanced JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Integer Answer Type Questions: Probability | JEE Advanced on the App
Students of JEE can study Integer Answer Type Questions: Probability | JEE Advanced alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Integer Answer Type Questions: Probability | JEE Advanced,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Integer Answer Type Questions: Probability | JEE Advanced is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup