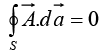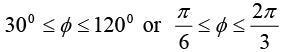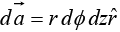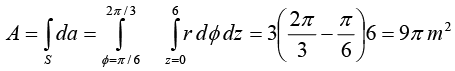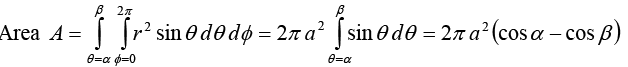Integral Calculus | Mathematical Methods - Physics PDF Download
Line, Surface, and Volume Integrals
(a) Line Integrals
A line integral is an expression of the form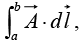
where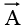 is a vector function,
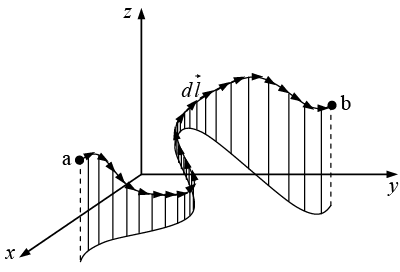
is a vector function,  is the infinitesimal displacement vector and the integral is to be carried out along a prescribed path P from point a to point b. If the path in question forms a closed loop (that is, if b = a), put a circle on the integral sign:
is the infinitesimal displacement vector and the integral is to be carried out along a prescribed path P from point a to point b. If the path in question forms a closed loop (that is, if b = a), put a circle on the integral sign: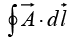
At each point on the path we take the dot product of 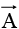 (evaluated at that point) with the displacement
(evaluated at that point) with the displacement 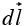 to the next point on the path. The most familiar example of a line integral is the work done by a force
to the next point on the path. The most familiar example of a line integral is the work done by a force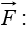
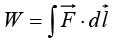
Ordinarily, the value of a line integral depends critically on the particular path taken from a to b, but there is an important special class of vector functions for which the line integral is independent of the path, and is determined entirely by the end points(A force that has this property is called conservative.)
Example 14: Calculate the line integral of the function 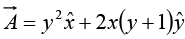 from the point a = (1, 1, 0) to the point b = (2, 2, 0), along the paths (1) and (2) as shown in figure. What is
from the point a = (1, 1, 0) to the point b = (2, 2, 0), along the paths (1) and (2) as shown in figure. What is 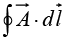 for the loop that goes from a to b along (1) and returns to a along (2)?
for the loop that goes from a to b along (1) and returns to a along (2)?
SincePath (1) consists of two parts. Along the “horizontal” segment dy = dz = 0, so
(i)
On the “vertical” stretch dx = dz = 0, so
(ii)
By path (1), then,
Meanwhile, on path (2) x = y, dx = dy, and dz = 0, so
so
For the loop that goes out (1) and back (2), then,
Example 15: Find the line integral of the vector 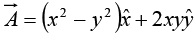 around a square of side ‘b’ which has a corner at the origin, one side on the x axis and the other side on the y axis.
around a square of side ‘b’ which has a corner at the origin, one side on the x axis and the other side on the y axis.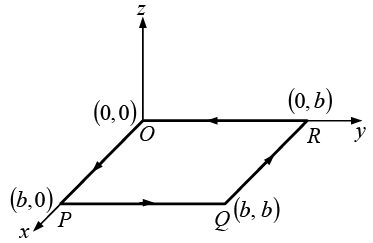
In a Cartesian coordinate syste
Along OP, y = 0, dy = 0 ⇒
Along PQ , x = b, dx = 0 ⇒
Along QR, y = b, dy = 0 ⇒
Along RO, x = 0, dx = 0 ⇒
Example 16: Compute the line integral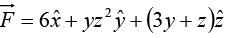 along the triangular path shown in the figure.
along the triangular path shown in the figure.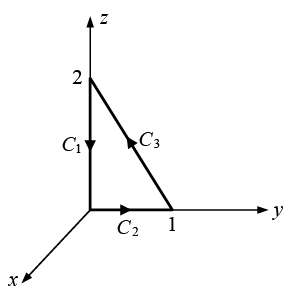
Line Integral
On path C1, x = 0, y = 0,
On path C2, x = 0, z = 0,
On path C3 the slope of line is -2 and intercept on z axis is 2 ⇒ z = -2y + 2 = 2 1 (1 - y) and the connecting points are (0, 1, 0) and (0, 0, 2)
On C3, x=0, dx = 0
Example 17: Given 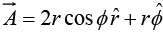 in cylindrical coordinates. Find
in cylindrical coordinates. Find 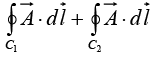 where c1 and c2 are contours shown in the figure.
where c1 and c2 are contours shown in the figure.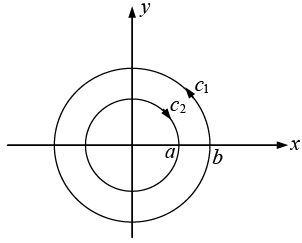
In cylindrical coordinate system
In figure on curve c1,Ф varies from 0 to 2π, r = b and dr = 0
On curve c2 , r = a,Ф varies from 0 to - 2π , and dr = 0 ⇒
So,
(b) Surface Integrals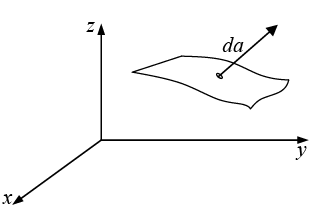
A surface integral is an expression of the form
where 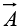 is again some vector function, and
is again some vector function, and 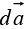 is an infinitesimal patch of area, with direction perpendicular to the surface(as shown in figure). There are, of course, two directions perpendicular to any surface, so the sign of a surface integral is intrinsically ambiguous. If the surface is closed then “outward” is positive, but for open surfaces it’s arbitrary. If
is an infinitesimal patch of area, with direction perpendicular to the surface(as shown in figure). There are, of course, two directions perpendicular to any surface, so the sign of a surface integral is intrinsically ambiguous. If the surface is closed then “outward” is positive, but for open surfaces it’s arbitrary. If 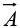 describes the flow of a fluid (mass per unit area per unit time), then
describes the flow of a fluid (mass per unit area per unit time), then 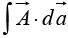 arepresents the total mass per unit time passing through the surface-hence the alternative name, “flux.”
arepresents the total mass per unit time passing through the surface-hence the alternative name, “flux.”
Ordinarily, the value of a surface integral depends on the particular surface chosen, but there is a special class of vector functions for which it is independent of the surface, and is determined entirely by the boundary line.
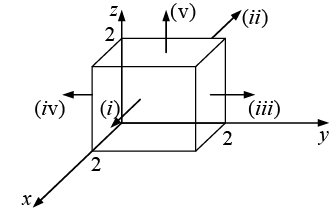
Example 18: Calculate the surface integral of A 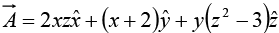 over five sides (excluding the bottom) of the cubical box (side 2) as shown in figure. Let “upward and outward” be the positive direction, as indicated by the arrows.
over five sides (excluding the bottom) of the cubical box (side 2) as shown in figure. Let “upward and outward” be the positive direction, as indicated by the arrows.
Taking the sides one at a time:

(i)
(ii)
(iii)
(iv)(v)
Evidently the total flux is
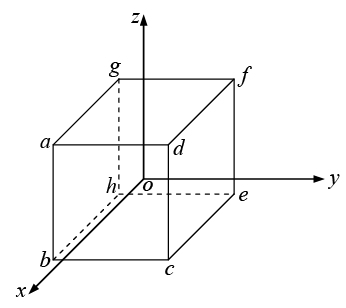
Example 19: Given a vector  Evaluate
Evaluate 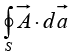 over the surface of the cube with the centre at the origin and length of side ‘a’.
over the surface of the cube with the centre at the origin and length of side ‘a’.
The surface integral is performed on all faces. The differential surface on the different faces are
Face abcd,
Face efgh,
Face cdfe,
Face aghb,
Similarly for the other two faces adfg and bceh we can find the surface integral withrespectively. The addition of these two surface integrals will be zero.
In the present case sum of all the surface integral
Example 20: Use the cylindrical coordinate system to find the area of a curved surface on the right circular cylinder having radius = 3 m and height = 6 m and 30º <∅ < 120º.
From figure, surface area is required for a cylinder when r = 3m, z = 0 to 6m,
In cylindrical coordinate system, the elemental surface area as scalar is
Taking the magnitude only
Example 21: Use spherical coordinate system to find the area of the strip  on the spherical shell of radius ‘a’. Calculate the area when α = 0 and β = π.
on the spherical shell of radius ‘a’. Calculate the area when α = 0 and β = π.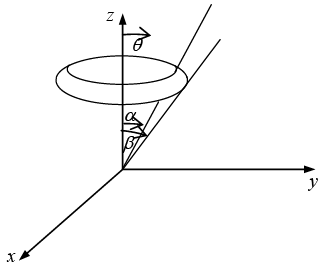
Sphere has radius ‘a’ and θ varies between α and β.
For fixed radius the elemental surface is da = (rsinθ d∅)(rdθ) = r2 sinθdθd∅
For α = 0, β = π, Area = 2πa2 (1 + 1) = 4πa2 , is surface area of the sphere.
(c) Volume Integrals
A volume integral is an expression of the form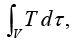
where T is a scalar function and dτ is an infinitesimal volume element. In Cartesian coordinates,
dτ = dx dy dz.
For example, if T is the density of a substance (which might vary from point to point) then the volume integral would give the total mass. Occasionally we shall encounter volume integrals of vector functions:
because the unit vectors are constants, they come outside the integral.
|
78 videos|18 docs|24 tests
|
FAQs on Integral Calculus - Mathematical Methods - Physics
| 1. What is integral calculus? |  |
| 2. What is the importance of integral calculus in IIT JAM exam? |  |
| 3. What are the basic integration techniques required for IIT JAM? |  |
| 4. How can I improve my skills in integral calculus for the IIT JAM exam? |  |
| 5. Can I score well in the IIT JAM exam without a strong grasp of integral calculus? |  |

|
Explore Courses for Physics exam
|

|
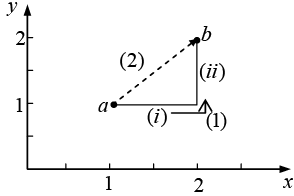
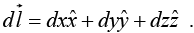 Path (1) consists of two parts. Along the “horizontal” segment dy = dz = 0, so
Path (1) consists of two parts. Along the “horizontal” segment dy = dz = 0, so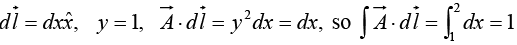
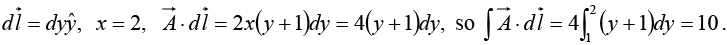
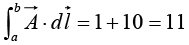
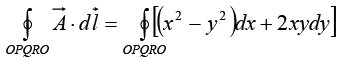
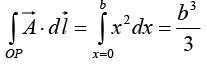
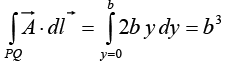
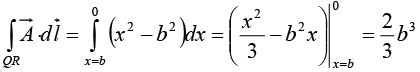
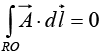
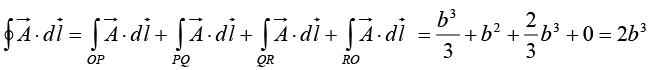
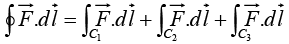

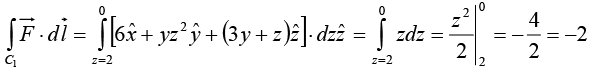
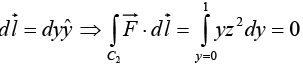
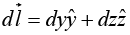
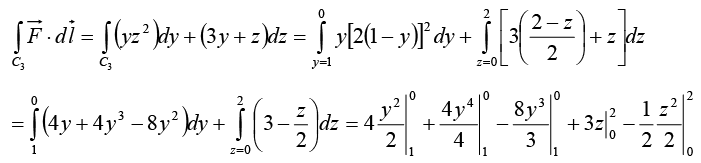
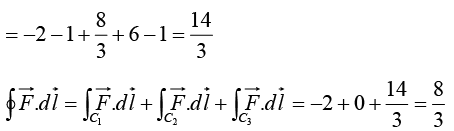
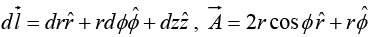
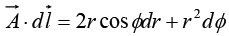
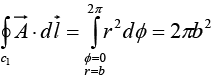
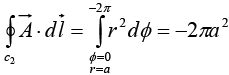
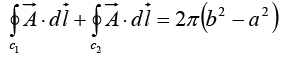
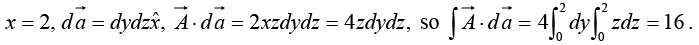
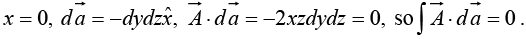
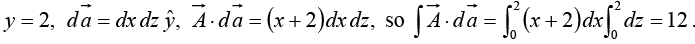
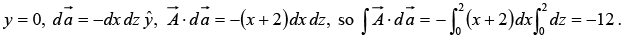
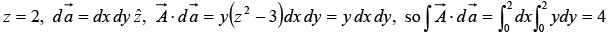
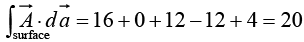
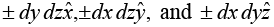 Face abcd,
Face abcd, 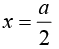
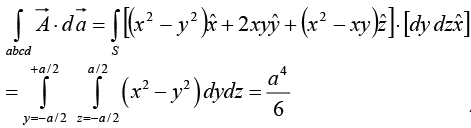
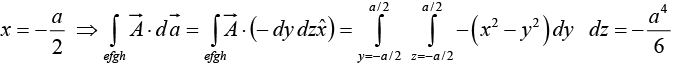
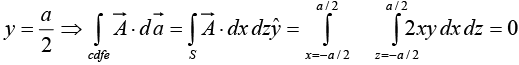
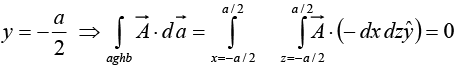
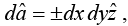 respectively. The addition of these two surface integrals will be zero.
respectively. The addition of these two surface integrals will be zero.