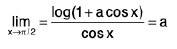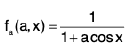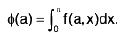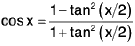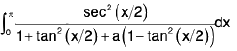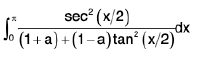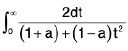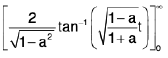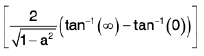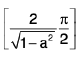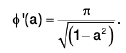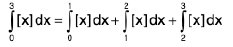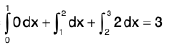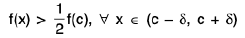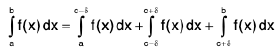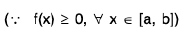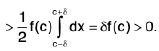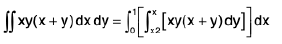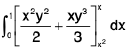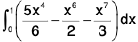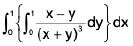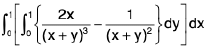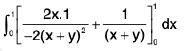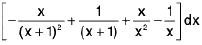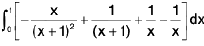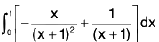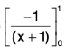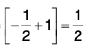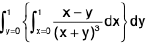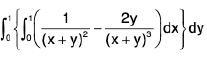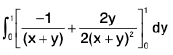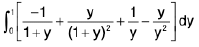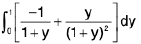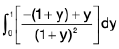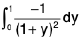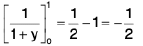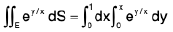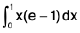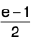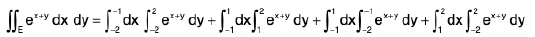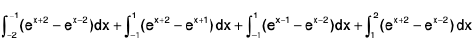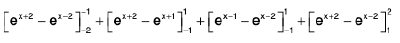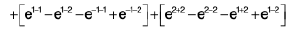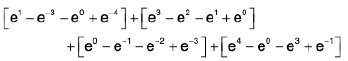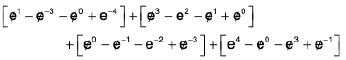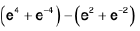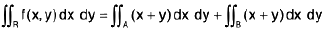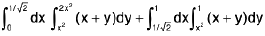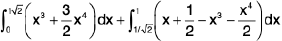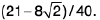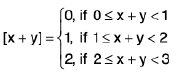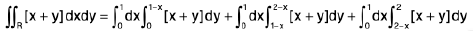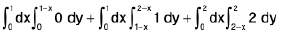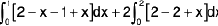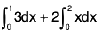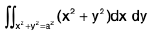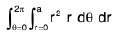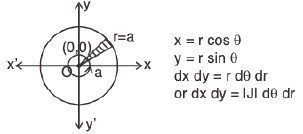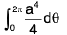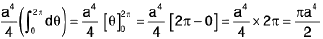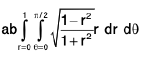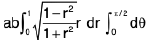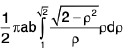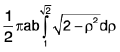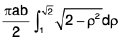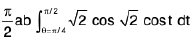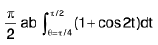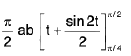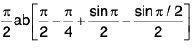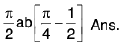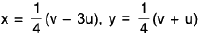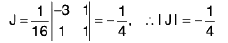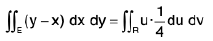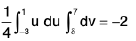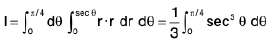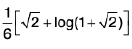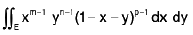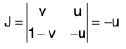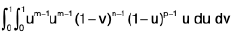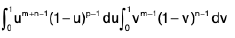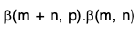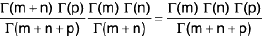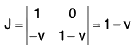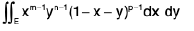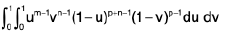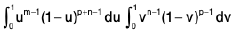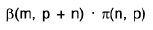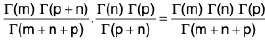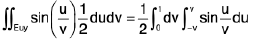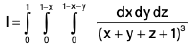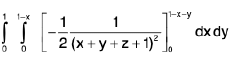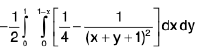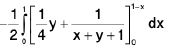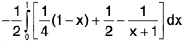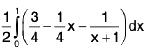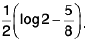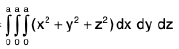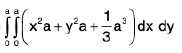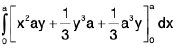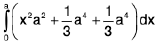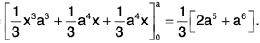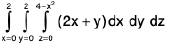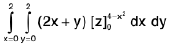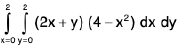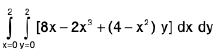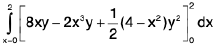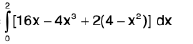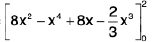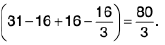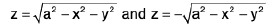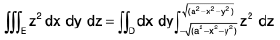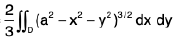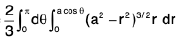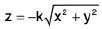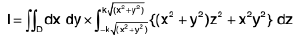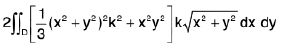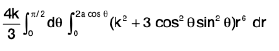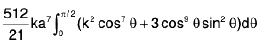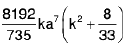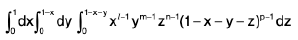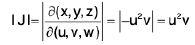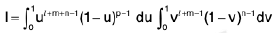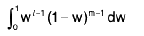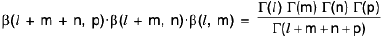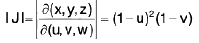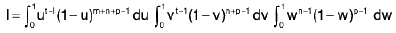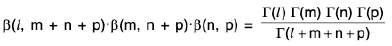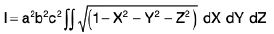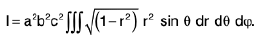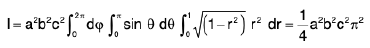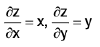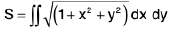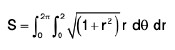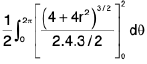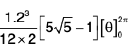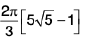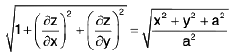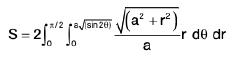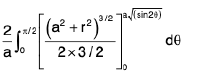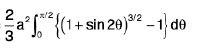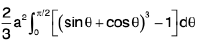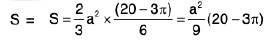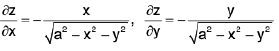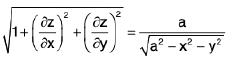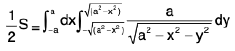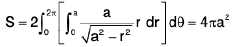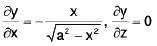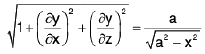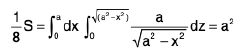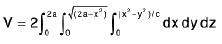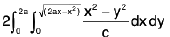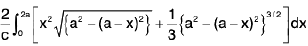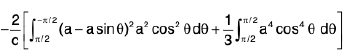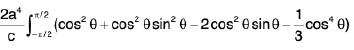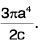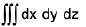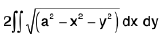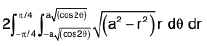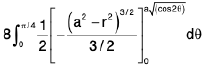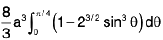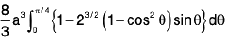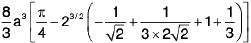Integral Calculus | Mathematics for Competitive Exams PDF Download
Differentiation Under the Integral Sign
In this section, we shall prove that, under suitable conditions, ‘the derivative of the integral and the integral of the derivative are equal’, and consequently, ‘the two repeated integrals are equal for continuous functions.’
Theorem (Leibnitz’s Rule). If f is defined and continuous on the rectangle R = [a, b; c d], and if
(i) fx(x, y) exists and is continuous on the rectangle R, and
(ii) g(x) = 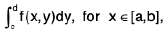
then g is differentiable on [a, b], and
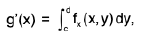
i.e., 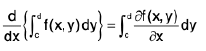
Corollary 1. (General Leibnitz’s rule). If f satisfy the conditions of the above theorem, and if
(i) θ, ψ : [a, b] → [c, d] are both differentiable, and
(ii) 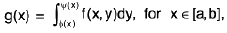
then g is differentiable on [a, b] and
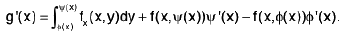
Corollary 2. If f is continuous on R = [a, b; c, d], then
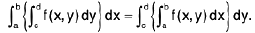
Iterated Integrals (or repeated integrals)
Definition. An iterated integral is an integral of the form
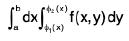
where θ1or θ2 or both are functions of x or constants.
This means that for each fixed x between a and b, the integral
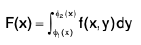
is evaluated, and then the integral 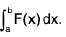
or 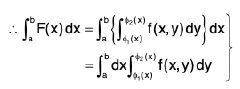 ----(1)
----(1)
The other repeated integral
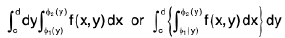 ---(2)
---(2)
is defined in the same way.
Example 1: If I a I < 1. show that
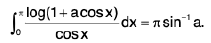
We write
It may be seen that the integrand has only a removable discontinuity at π/2 as much as
Also
We see that f and fa are both continuous functions of two variables in the domain {(a,x) : 0 ≤ x ≤ π, I a I < 1}. If we assign to f, the value a for x = π/2.
We write
⇒
----(1)
Put
put tan (x/2) = t
diff w. r. to x we get
sec2(x/2).1/2 dx = dt
=
=
=
=
Therefore,
⇒
From this we obtain
∅(a) = πsin-1 a + c. . ..( 2 )
where, c, is an arbitrary constant.
From (1), we have
∅(0) = 0.
Putting a = 0 in (2), we obtain c = 0.
Hence ∅(a) = πsin-1 a.
Fundamental Theorem of Calculus
Theorem : If a function f is bounded and integrable on [a, b], then the function F defined as
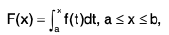
is continuous on [a, b], and furthermore, if f is continuous at a point c of [a, b], then F is derivable at c and
F’(c) = f(c).
Since f is bounded therefore ∃ a number K > 0 such that
I f(x) I < K, ∀ x ∈ [a, b].
If x1, x2 are two points of [a, b] such that a ≤ x1 < x2 ≤ b, then
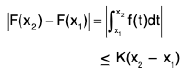
Thus for a given ∈ > 0, we see that
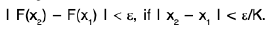
Hence the function F is continuous (in fact uniformly) on [a, b].
Let f be continuous at a point c of [a, b], so that for any ∈ > 0 there exists δ > 0 such that
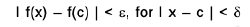
Let c - δ < δ < c < t < c + δ
∴ 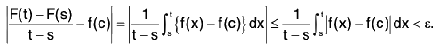
⇒ F'(c) = f(c).
i.e., continuity of f at any point of [a, b] implies derivability of F at that point.
Note. As c is any point of [a, b], we have for all x ∈ [a, b],
F’(t) = f(t) ⇒ F = f
i.e.; continuity of f on [a, b] implies derivability of F on [a, b].
This theorem is sometimes referred to as the First Fundamental Theorem of Integral Calculus.
Definition : A derivable function F, if it exists such that its derivative F’ is equal to a given function f, is called a primitive of f.
The above theorem shows that a sufficient condition for a function to admit of a primitive is that it is continuous. Thus every continuous function f possesses a primitive F where
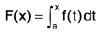
Remark : We shall now show, with the help of an example, that continuity of a function is not a necessary condition for the existence of a primitive, in other words, “functions possessing primitives are not necessarily continuous”.
Consider the function f on [0, 1], where
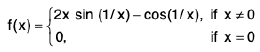
It has a primitive F. where
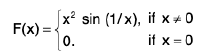
Clearly F’(x) = f(x) but f(x) is not continuous at x = 0, i.e., f(x) is not continuous on [0, 1] In fact, all this amounts to saying that the derivative of a function is not necessarily continuous.
Theorem : Function f is bounded and integrable on [a, b] and there exists a function F such that F’ = f on [a, b], then
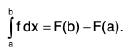
Since the function F'. f is bounded and integrable, therefore for every given ∋ > 0, ∃ δ> 0 such that for every partition P = { a = x0 x1 ..x2..... xn = b}. with norm μ(p) < δ,
or 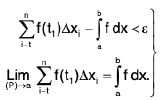 ----(1)
----(1)
for every choice of points t1 in Δx1..
Since we have freedom in the selection of points tt Δxt, we choose them in a particular way as follows:
By Lagrange’s mean value theorem, we have
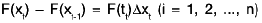
= 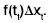
⇒ 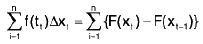
= F(b) - F(a).
Hence from (1).
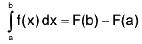
It is sometimes referred to as The second Fundamental Theorem of Integral Calculus.
Example 2 : Show that the function [x], where [x] denotes the greatest integer not greater than x, is integrable in [0, 3].
Since the function is bounded and has only three points of discontinuity therefore it is integrable and
=
1, 2 and 3 being respectively the points of discontinuity of the three integrals on the right.
Example 3 : f is a non-negative continuous function on [a, b] and 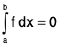 . Prove that f(x) = 0, for all x e∈ [a, b].
. Prove that f(x) = 0, for all x e∈ [a, b].
Suppose that, for some c ∈ (a, b), f(c) > 0
Then, for
continuity of f at c implies that, there exists a δ > 0 such that
Now
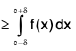
which is a contradiction. Thus f(x) = 0, ∀ x ∈ (a, b).
Similarly, f(a) > 0, and f(b) > 0. Hence the result follows.
Double Integral
The Calculation of a double integral
Equivalence of a double with repeated integrals.
Theorem. If the double integral
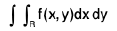
exists where R is the rectangle [a, b; c, d]
and if also 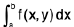 exist ∀ y ∈ [c, d],
exist ∀ y ∈ [c, d],
then the repeated integral
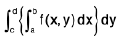
exists and is equal to the double integral.
Definite Double Integral : If we have function f(x, y) then
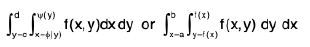
If dx first then function of y is constant and if dy first then function of x is constant.
Cor. If a double integral exists, then the two repeated integrals cannot exist without being equal.
Cor. A function f is defined in [0, 1; 0, 1] as-follows :
f(x, y) = 1/2, when y is rational,
f(x, y) = x, when y is irrational;
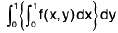 exists and is equal to 1/2, but the double integral and the second repeated integral do not exist.
exists and is equal to 1/2, but the double integral and the second repeated integral do not exist.
Example 4 : Evaluate 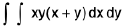 over the area between y = x2 and y = x.
over the area between y = x2 and y = x.
The area is bounded by the curves
y = f1(x) = x2, y = f2(x) = x. see in fig.
When f1(x) = f2(x), x2 = x, i.e., x = 0, x = 1, i.e., the area of integration is bounded by
y = x2, y = x, x = 0 , x = 1
In fig. x varies from x = 0 to x = 1 and y varies from y = x2 to y = x
∴
=
=
= 3/56
Example 5 : Prove that
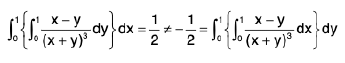
LHS =
=
=
=
=
=
=
=
=
RHS =
=
=
=
=
=
=
=
LHS ≠ RHS
Change of Order of Integration
In calculus, interchange of the order of integration is a methodology that transforms iterated integrals of functions into other.
Theorem : If S is a region of Type I, then

If S is a region of Type II, then
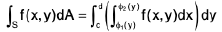
We should point out that, unlike the case of integrals over rectangles, there is only one order in which we can carry out the integrations. If S is a Type I region we have to integrate over y before we integrate over x and if S is a Type II region we have to carry out the integration over x before we integrate over y.
However, sometimes a region is both Type I and Type II. This does not mean that
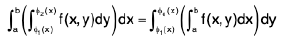
because the right hand side doesn’t really make any sense. Rather, it means that we can prescribe the region S in two different ways
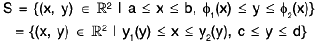
The preceding theorem applied to this situation simple says
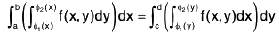
In order to reverse the order of integration of an integral like
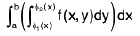
one therefore first has to Fig. out how to parameterize the region of integration
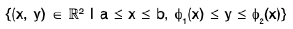
as a Type II region; that is to say, one has to Fig. out what c, d, ψ1(y), and ψ2(y) are.
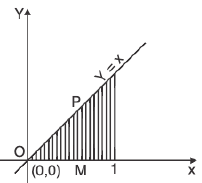
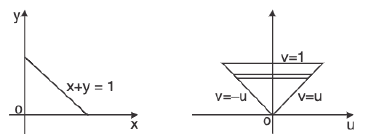
Example 6 : Find the value of 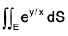 if the domain E integration is the triangle bounded by the straight lines y = x, y = 0 and x = 1.
if the domain E integration is the triangle bounded by the straight lines y = x, y = 0 and x = 1.
How to take limit of y and x, we draw a strip parallel to y axis in the fig.
Now lower end of strip is on the line y = 0 and upper end of strip is on the line y = x So y varies from y = 0 to y = x.
For x, we pull the strip at the left end of shaded fig i.e. x = 0 and extend the strip i.e the right end of shaded region i.e. x = 1 So y varies from y = 0 to x.
To avoid integration of ey/x with respect to x, we use
=
=
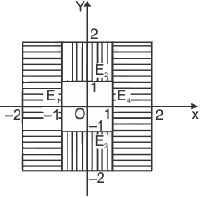
Example 7 : Evaluate the double integral 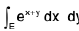 , when E is the domain which lies between two squares of sides 2 and 4, with center at the origin and sides parallel to the axes.
, when E is the domain which lies between two squares of sides 2 and 4, with center at the origin and sides parallel to the axes.
Domain E is not quadratic with respect to any axes but the straight lines x = -1, x = 1 divide it into four quadratic domains, E1, E2, E3, E4.
see the region E1, limit of x is from -2 to -1 and limit of y is from -2 to 2 Similarly find limits for other regions also.
∴
=
=
=
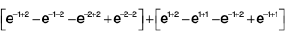
=
=
== 2 cosh(4) - 2 cosh(2)
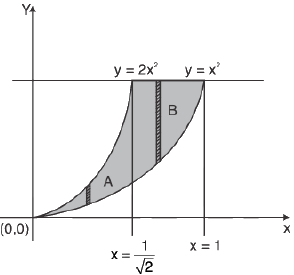
Example 8 : Evaluate 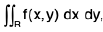 , over the rectangle R = [0, 1; 0, 1], where
, over the rectangle R = [0, 1; 0, 1], where
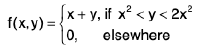
For non-zero values of the function f(x, y), the domain R is divided into two domains A and B, we obtain
=
=
=
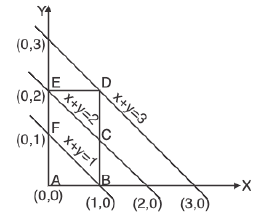
Example 9 : Evaluate 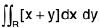 , over the rectangle R = [0, 1 : 0, 2], where [x + y] denotes the greatest integer less than or equal to (x + y). We have, for (x, y) ∈ R.
, over the rectangle R = [0, 1 : 0, 2], where [x + y] denotes the greatest integer less than or equal to (x + y). We have, for (x, y) ∈ R.
The domain of integration R (i.e. region ABDE) is divided into three domains ABF, BCEF and CDE and [x + y] = 0 in the region ABF, [x + y] = 1 in region BCEF and [x + y] = 2 in the region CDE.
Therefore, we have
=
=
=
= 3 [1 - 0] + 2 [2 - 0]
= 3 + 4 = 7
Jacobian of Transformation
f(x, y)dx dy = f(r cosθ, r sinθ) Jdr dθ
dx dy = Jdr dθ
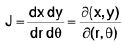
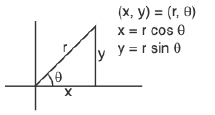
∴ 
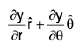
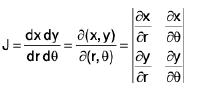
which is known as Jacobian.
Jacobian of transformation form of (x, y) into (r, θ)
J = 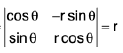
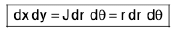
Change of Variables in Double Integrals
Let the functions x = X(u, v); y = Y(u, v) map in one-to-one manner a domain D in Cartesian coordinates (x, y) onto a domain D’ in the new coordinates u, v.
Let f(x, y) = f(X(u, v), Y(u, v)) = F(u, v)
Then 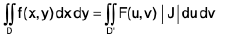
where the Jacobian J = 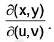
In case of a transformation from a Cartesian coordinate system (x, y) to polar coordinate system (r, θ); I f I = r, and hence dx dy = r dθ dr.
Change of Variables in Triple Integrals
Let the functions
x = X(u,v,w), y = Y(u,v,w), z = Z(u,v,w)
map in one-to-one manner, a domain D in cartesian coordinates (x,y,z) onto a domain D’ in the new variables (u,v,w)
Let f(x,y,z) = f(X(u,v,w), Y(u,v,w), Z(u,v,w)) = F(u,v,w)
Then 
where the Jacobian J = 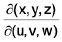 (matrix is same as given by eq. (1) of order 3)
(matrix is same as given by eq. (1) of order 3)

The following two transformations because of their frequent occurrence, deserve special mention
(i) Cylindrical polar coordinates
x = r cosθ, y = r sinθ, z = z Here the Jacobian J = r.
ii) Spherical polar coordinates. x = r sinθ cos ∅, y = r sinθ sin ∅, z = r cosθ
Here the Jacobian J = r2 sinθ
Examples 10 : To integrate (x2 + y2) over the circle x2 + y2 = a2, we change to polar, x = r cosθ, y = r sinθ, so that 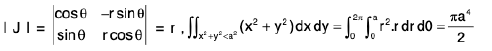 .
.
(integrating wrt r)
=
1. To evaluate
over the positive quadrant of the ellipse x2/a2 + y2/b2 = 1, by putting x = au ⇒ d x = a du, and y = bv = > d y = bdv, we have to evaluate ab
dv, over the positive quadrant of the circle u2 + v2 = 1.
Again, changing to polars, by putting u = r cos 0, v = r sin 0, the integral becomes
=
=
put 1 + r2 = p2 ⇒ 2rdr = 2pdp (lim it: r = 0 ⇒ p = 1, r = 1⇒ p = √2 )
=
=
put p = √2 sint
dp = √2 cost dt
=
Put p = √2 sin t
dp = - √2 cost dt
=
=
=
=
=
=
Note : The transformation could be effected in one step by putting x / a = rcosθ, y /b = rsinθ, then I J I = abr.
2. To evaluate ∫∫{ 2a2 - 2a( x + y) - ( x2 + y2) } dx dy over the circle x2 + y. + 2a(x + y) = 2a2, transform the origin to ( - a, - a ), by putting x + a = u, y + a = v, so t hat the integral becomes ∫∫( 4a2 - u. - v2) dudv, over the circle u2 + v2 = 4a2. Changing to polars , we get 8πa4.
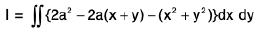 over the circle
over the circle
x2 + y2 + 2a(x + y) = 2a2
x2 + 2ax + a.+ y2 + 2ay + a2 = 4a2
(x + a)2 + (y + a)2 = 4a2
put x + a = u, y + a = v
So the integral becomes

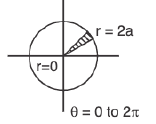
Changing into polar coordinates
= 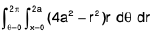
= 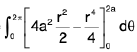
= 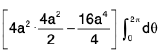
= 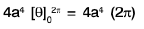
= 8πa4
Example 11 : Evaluate ∫ ∫y - x ) d x dy, over the region E in the xy-plane bounded by the straight lines y = x - 3 , y = x+1,3y + x = 5,3y + x = 7
It is difficult to evaluate the double integral directly; however a simple change of coordinates reduces the domain of integration into a rectangle with sides parallel to the axis.
Set y - x = u, 3y + x = v
so that
and
The new domain is the rectangle R = [-3, 1; 5, 7] in uv-plane.
∴
=
Example 12 : Evaluate the integral 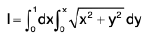 by passing on to the polar coordinates.
by passing on to the polar coordinates.
The integral in question is the double integral
dx dy over the region enclosed by the triangle y = 0, y = x, x = 1.
In polar coordinates, the equations of these lines are 0 = 0, 0 = rc/4. r cos 0 = 1, so that the domain of integration is 0 < 0 <π/4, 0 < r < sec 0.
∴
=
Dirichlet's Theorem
The theorem states that
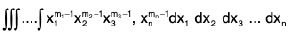
= 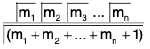
where the integral is extended to all +ve values of the variables x1, x2, ..., xn subject to the condition x1 + x2 + ..., xn ≤ 1.
Liouville's Extension of Dirichlet's Theorem
If x, y, z all positive such that
h,≤ x + y + z ≤ h2
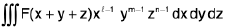
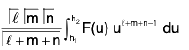
Example 13 : Evaluate 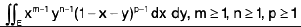 where E is the region bounded by x = 0, y = 0, x + y = 1.
where E is the region bounded by x = 0, y = 0, x + y = 1.
Now
=
For this type of integrals, two sets of substitutions are possible, which give an integral with constant limits. We discuss both these here.
First method. Put x + y = u, x = uv
so that y = u(1 - v) and
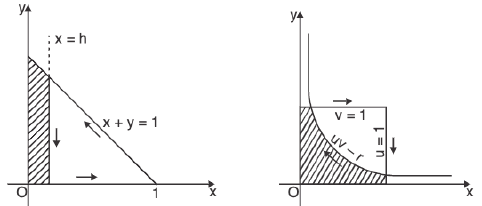
The Jacobian vanishes when u = 0, i.e., when x = 0 = y. The origin of the xy-plane corresponds to the whole line u = 0 of the uv-plane, so that the correspondence ceases to be one-to-one. To exclude the origin of the xy-plane, we cut out the region along a line x = h parallel to the y-axis and consider the integral on the remaining domain E,, bounded by the lines
v = 1, u = 1, uv = h
However, in the limit when h -> 0, this new region degenerates into the square bounded by v = 1, u = 1, v = 0, u = h
Thus
=
=
=
=
Second method. Put x = u, y = (1 - u)v, so that
1 - x - y = 1 - u - ( 1 - u ) v = (1 - u)(1 - v )
and
which vanishes for u = 1, so that the point (1, 0) in the xy-plane corresponds to the whole line u = 1 in the uv-plane. However, proceeding as in the first method, the new region becomes the square.
u = 0, v = 0, u = 1, v = 1
Thus
=
=
=
=
Example 14 : Evaluate 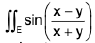 dxdy, where E is the region bounded by the co-ordinate axes and x + y = 1 in the first quadrant.
dxdy, where E is the region bounded by the co-ordinate axes and x + y = 1 in the first quadrant.
Taking x - y = u, x + y = v, so that x = 1/2(u+v), y = 1/2(v-u) and the Jacobian is 1/2.
∴
-------(1)
Now
=
----(2)
Hence, from (1) and (2), the required integral is zero.
Triple Integrals
Let f(x, y, z) be a function of three independent variables x, y and z defined at every point of a three-dimensional region V. Divide the region V into n elementary volumes δV1f δV2, δVn and let (xr, yr, zr) be any point inside the rth sub-division δVr. Find the sum
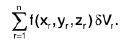
Then 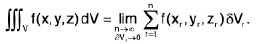
To extend definition of repeated integrals for triple integrals, consider a function f(x, y, z) and keep x and y constant and integrate with respect to z between limits in general depending upon x and y. This would reduce f(x, y, z) to a function of x and y only. Thus, let
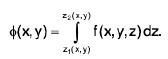
Then in ∅ (x, y) we can keep x constant and integrate with respect to y between limits in general depending upon x this leads to a function of x alone, say
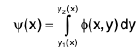
Finally ψ(x) is integrated with respect to x assuming that the limits for x are from a to b.
Thus
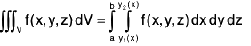
= 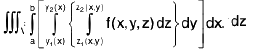
If we put f(x, y, z) = 1, then the volume
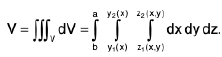
Use of definite triple integral in finding volume of 3D shape :
If we have a 3D-shape in which two very-very closed point (P, Q) are taken as diagonal of a cuboid.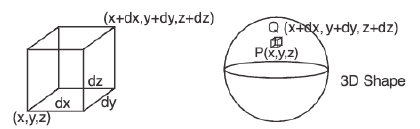
Then volume of this elementary cuboid inside that 3D shape
dV = dx dy dz
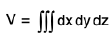 taken over region
taken over region
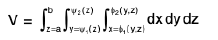
Example 15 : Evaluate the integral 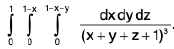
Let
=
=
=
=
=
=
=
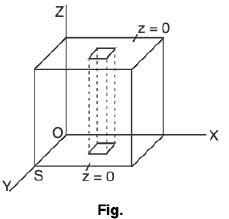
Example 16 : Evaluate 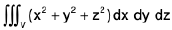 here V is the volume of the cube bounded by the coordinate planes and the planes x = y = z = a.
here V is the volume of the cube bounded by the coordinate planes and the planes x = y = z = a.
Here a column parallel to z-axis is bounded by the planes z = 0 and z = a.
Here the region S above which the volume V stands is the region ist he xy-plane bounded by the lines x = 0, x = a, y = 0, y = a.
Hence the given integral
=
=
=
=
=
=
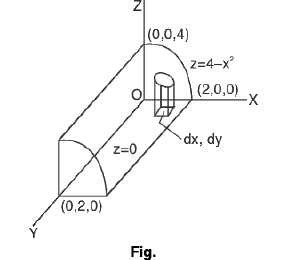
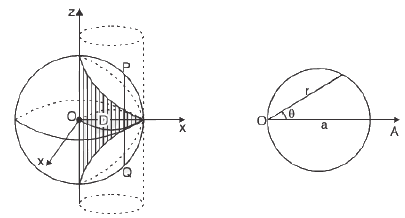
Example 17 : 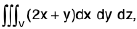 where V is the closed region bounded by the cylinder z = 4 - x2 and the planes x = 0, y = 0, y = 2 and z = 0.
where V is the closed region bounded by the cylinder z = 4 - x2 and the planes x = 0, y = 0, y = 2 and z = 0.
Here a column parallel to z-axis is bounded by the plane z = 0 and the surface z = 4 - x2 of the cylinder.
This cylinder z = 4 - x2 meets the z-axis, x = 0, y = 0, at (0, 0, 4) and the x-axis, y = 0, z = 0 at (2, 0, 0) in the given region.
Therefore, it is evident that the limits of integration for z are from 0 to 4 - x2, for y from 0 to 2 and for x from 0 to 2.
Here the given integral
=
=
=
=
=
=
=
=
Example 18 : Evaluate 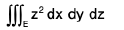 taken over the region common to the surfaces x2 + y2 + z2 = a2, and x2 + y2 = ax
taken over the region common to the surfaces x2 + y2 + z2 = a2, and x2 + y2 = ax
The region is bounded, above and below by the surfaces
and its projection on the xy-plane is the circular domain D = x2 + y2 ≤ ax.
∴
=
Changing to polars, the region D becomes the circle, r = a cosθ
0 ≤ θ ≤ π, 0 ≤ r ≤ a cosθ
=
=
Example 19 : Evaluate 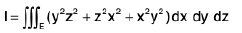 taken over the domain bounded by the cylinder x2 + y2 = 2ax, and the cone z2 = k2(x2 + y2).
taken over the domain bounded by the cylinder x2 + y2 = 2ax, and the cone z2 = k2(x2 + y2).
The domain E is bounded above and below by the surface
and
and its projection on the xy-plane is the circular domain D, x2 + y2 ≤ 2ax.
∴
=
Changing to polars,
=
=
=
Change of Variables in A Triple Integral
Let f be continuous in a domain E bounded by a surface S in xyz-space.
Also let
x = x (X, Y, Z), y = y (X, Y, Z); z = z (X, Y, Z).
define three functions of three variables X, Y, Z, defined in a domain E, bounded by a surface S, in XYZ-space.
We suppose that these three functions with values
x (X, Y, Z), y(X, Y, Z), z(X, Y, Z)
(i) possess continuous first order partial derivatives at each point of E, and Sr
(ii) transform E, into E and S1 into S.
(iii) the transformation is one-one.
(iv) the Jacobian

does not change sign at any point of E1, even though it may vanish at some points of S1 It will then be proved that
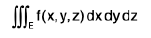
= 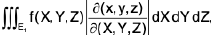
where x, y, z have to be replaced by their values in terms of X, Y, Z in f(x, y, z) in the integral on the right.
Example 20: Show that 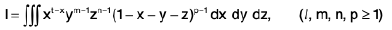 taken over the tetrahedron bounded by the planes, x = 0, y = 0, z = 0,
taken over the tetrahedron bounded by the planes, x = 0, y = 0, z = 0, 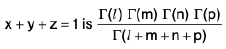
The given integral is same as
First Method . Let us put x + y + z = u, x + y = uv, x = uvw, i.e., std. substitution
x = uvw, y = uv(1 - w), z = u(1 - v)
It may be seen that when x, y, z are positive and x + y + z < 1, then each of u, v, w lie between 0 and 1 and conversely. So the given region is fully described when 0 ≤ 1 , 0 ≤ v ≤ 1 , 0 ≤ w ≤ 1 .
Also, them
∴
=
Second Method . Put x = u, y = (1 - u)v, z = (1 - u) (1 - v)w so that
1 - x - y - z = ( 1 - u)(1 - v)(1 - w)
and
∴
=
Example 21 : Evaluate 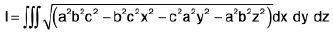 taken throughout the domain
taken throughout the domain 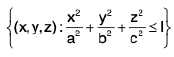
Change the variables x, y, z to X, Y, Z where x = aX, y = bY, z = cZ,
so that ∂(x, y, z)/∂(X, Y, Z) = abc.
Thus
taken throughout X2 + Y2 + Z2 ≤ 1.
Changing X, Y, Z to polar co-ordinates r, θ, φ so that X = r sinθ cosφ, Y = r sinθ sinφ, Z = r cosθ,
We have, since
∂(X, Y, Z)/∂(r, θ, φ) = r2 sin θ,
It is easily seen that to describe the whole region.
X2 + Y2 + Z2 ≤ 1.
r varies from 0 to 1; 0 varies from 0 to π ; φ varies from 0 to 2π.
Thus (r, 0, φ) varies in the rectangular parallelepiped.
[0, 1; 0, π; 0, 2π]
∴
SURFACE AREA
Definition : The area of the surface
x = f(u, v), y = g(u, v), z = h(u, v); (u, v) ∈ D is the double integral
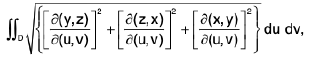 assuming that the functions f, g, h possess continuous first order partial derivatives in D and at no point of D.
assuming that the functions f, g, h possess continuous first order partial derivatives in D and at no point of D.
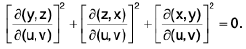
Note : Here, we do not propose to derive the expression as given above by basing the derivation on some elementary notion of surface area. Let the definition as given appear very arbitrary, we outline some considerations to call forth reader’s faith in the same.
I. Let the surface be plane. We take
x = u, y = v, z = 0
where (u, v) ranges over a domain D in the XY-plane. In fact, the surface coincides with D in the present case.
We have
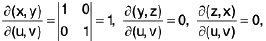
∴ 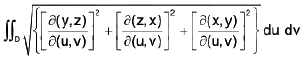
= 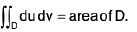
Thus the definition of surface area as now given agrees with that of areas of plane regions.
II. Consider the surface given by z = h (x, y).
We take it as given by
z = u, y = v, z = h(u, v)
where (u, v) = (x, y) ∈ D ⊂ R3.
We have
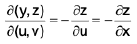

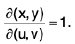
∴ surface area = 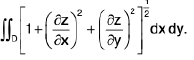 -----(1)
-----(1)
The reader acquainted with the elements of Differential Geometry knows that
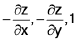 are the direction ratios of the normal to the surface at any point (x, y, z) , so that if we suppose δσ to be an element of surface lying on the tangent plane at the point, the projection area δA of δσ on the XY-plane is given by
are the direction ratios of the normal to the surface at any point (x, y, z) , so that if we suppose δσ to be an element of surface lying on the tangent plane at the point, the projection area δA of δσ on the XY-plane is given by
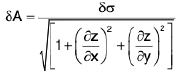
⇒ 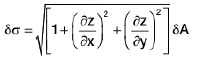
= 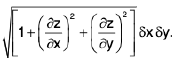
This suggests, on summation, the truth of (1).
Note. The reader may easily show that
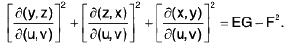
where E = 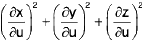
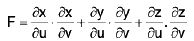
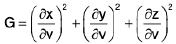
Smooth surface.
Definition: A surface given by x = f(u, v), y = g(u, v), z = h(u, v); (u, v) ∈ D is said to be smooth, if f, g, h possess continuous first order partial derivatives at each point of D and at no point there of
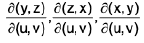 vanish simultaneously.
vanish simultaneously.
Example 22: The area of the surface of the paraboloid 2z = x2 + y2 which lies between the planes z = 0, z = 2 is ______
Here
∴
The projection on the plane z = 2 is x2 + y2 = 4 or r = 2 which is a circle between θ = 0 and θ = 2π (changing to polars by putting x = r cos θ, y = r sinθ). Hence
=
=
=
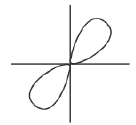
Example 23 : Find the area of the surface az = xy that lies inside the cylinder (x2 + y2)2 = 2a2xy.
We have az = xy.
∴
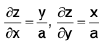
Surface area =
=
changing into polars .(x2 + y2 =r2 , x = r cosθ , y = r sinθ )
Also (x2 + y2)2 = 2a2xy becomes r2 = a2 sin 2θ curve is a symmetric about origin and see the loop of the curve lies between θ= 0 to π/2.
∴
=
=
=
-------(1)
where
------(2)
By equation (i),
Example 24 : Compute the surface area S of the sphere x2 + y2 + z2 = a2
The surface area of the sphere is twice the surface are a of the upper half-sphere
z =
Now
so that
The domain of integration is the circle x2 + y2 = a2 on the xy-plane.
Thus by formula (1), we have
On passing to polars, we have
Example 25 : Find the area of that part of the surface of the cylinder x2 + y2 = a2 which is cut out by the cylinder x2 + z2 = a2.
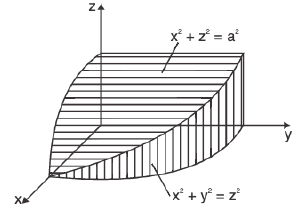
The Fig. shows 1/8th of the desired surface
The equation of the surface has the form
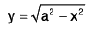
so that
The domain of integration is a quarter circle x2 + z2 = a2, x ≥ 0, z≥ 0, on the xz-plane. Thus by formula (3), we have
∴ S = 8a2.
Evaluation of Volumes
By Triple Integration
The triple integral
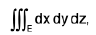
carried throughout a region E in space of three dimensions gives the volume of E.
By Double Integration Let C be the boundary of a region E of the xy-plane and let a cylinder be constructed by lines through the points of C parallel to z-axis. Then the volume of the cylinder enclosed between the surfaces
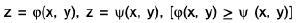
is 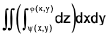 and can be easily seen. given by the double integral
and can be easily seen. given by the double integral
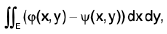
Example 26: The volume enclosed by the surfaces x2 + y2 = cz, x2 + y2 = 2ax, z = 0.
The limits of z are 0 to 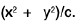 The limits of y are from
The limits of y are from 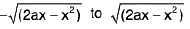 and the limits of x are from 0 to 2a.
and the limits of x are from 0 to 2a.
The value
=
=
=
Put a - x = a sin θ
=
=
=
Example 27 : The sphere x2 + y2 + z2 = a2 is pierced by the cylinder (x2 + y2)2 = a2(x2 - y2); prove that the volume of the sphere that lies inside the cylinder is 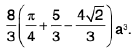
Here limits of z are from
and therefore
the volume =
=
Now the equation of the cylinder is
(x2 + y2)2 = a2(x2 - y2)
Putting x = r cosθ, y = r sinθ, we get
r2 = a2 cos2θ.
∴ The limits of r are from
and limits of 0 are from -π/4 to π/4.
∴ The required volume
=
=
=
=
=
=
|
98 videos|34 docs|32 tests
|
FAQs on Integral Calculus - Mathematics for Competitive Exams
| 1. What is the concept of differentiation under the integral sign? |  |
| 2. How are iterated integrals used in calculus? |  |
| 3. What does the Fundamental Theorem of Calculus state? |  |
| 4. How are double integrals used in calculus? |  |
| 5. What is the concept of change of variables in a triple integral? |  |