Integrated Rate Law Expression of Zero Order Reaction | Physical Chemistry PDF Download
Integrated Rate Law Expressions
Integrated rate law expression provides the predicted temporal evolution in reactant and product concentrations for reactions having an assumed order dependence.
Zero-Order Reaction
- The rate of reaction is independent of the concentration of the reactants in these reactions.
- A change in the concentration of the reactants has no effect on the speed of the reaction
- Examples of these types of reactions include the enzyme-catalyzed oxidation of CH3CH2OH (ethanol) to CH3CHO (acetaldehyde).
Consider the following elementary reaction
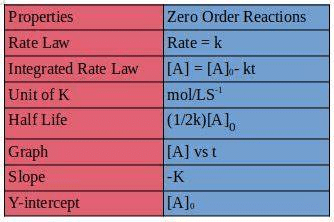
For zero-order reaction, the rate law is
k is rate constant.
⇒ –d[A] = k dt
If at t = 0, the initial concentration is [A]0 and the concentration at t = t, is [A], then integration yields
⇒ [A]0 – [A] = kt
This is an integrated rate equation for a zero-order reaction in terms of reactant.
= k d[P] = k dt
at t = 0, [P] = 0
and at t = t, [P] = [P]
then integration yields
[P] = kt
This is an integrated rate law equation for a zero-order reaction in terms of product.
i.e. [A]0 – [A] = kt = [P]
Graphical Representation of Zero-Order Reaction
Graph of Reactant vs Time.
[A]0 – [A] = kt
[A] = –kt + [A]0
y = mx + c
Graph of Product vs Time.
[P] = kt
y = mx
Concentration of Product vs Time.
[A]0 – [A] = 2kt …(i)
When t = 0 then [P] = 0 and t = t then [P] = [P]
[P] = 3kt …(ii)
…(iii)
Problem. Find the integrated rate law expression for an elementary zero-order reaction given below.
Sol.
The rate law of the above elementary reaction is given below
⇒
⇒ – [[A] – [A]0] = kt
[A]0 – [A] = kt …(i)
⇒ …(ii)
⇒
[P] = kt …(iii)
From equation (i), (ii) & (iii) we get
|
84 videos|142 docs|67 tests
|
FAQs on Integrated Rate Law Expression of Zero Order Reaction - Physical Chemistry
| 1. What is the integrated rate law expression for a zero-order reaction? |  |
| 2. How can the rate constant be determined for a zero-order reaction? |  |
| 3. Is the half-life of a zero-order reaction constant? |  |
| 4. Can the integrated rate law expression for a zero-order reaction be used to determine the reaction order? |  |
| 5. How does the rate of a zero-order reaction change with changes in reactant concentration? |  |

















