Integration by parts method, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com PDF Download
Integration by Parts
Integration by Parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways.
You will see plenty of examples soon, but first let us see the rule:
- u is the function u(x)
- v is the function v(x)
As a diagram
Let's get straight into an example, and talk about it after:
Example: What is 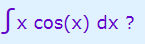 ?
?
OK, we have x multiplied by cos(x), so integration by parts is a good choice.
First choose which functions for u and v:
- u = x
- v = cos(x)
So now it is in the format we can proceed:
Differentiate u: u' = x' = 1
Integrate v: (see Integration Rules)
Now we can put it togethe
Simplify and solve:
x sin(x) − ∫sin(x) dx
x sin(x) + cos(x) + C
So we followed these steps:
- Choose u and v
- Differentiate u: u'
- Integrate v:
- Put u, u' and ∫v dx into:u
- Simplify and solve
In English, to help you remember, becomes:
(u integral v) minus integral of (derivative u, integral v)
Let's try some more examples:
Example: What is 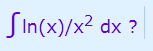
First choose u and v:
- u = ln(x)
- v = 1/x2
Differentiate u: ln(x)' = 1/x
Integrate v: (by the power rule)
Now put it together:
Simplify:
− ln(x)/x −
− (ln(x) + 1)/x + C
Example: What is
But there is only one function! How do we choose u and v ?
Hey! We can just choose v as being "1":
- u = ln(x)
- v = 1
Differentiate u: ln(x)' = 1/x
Integrate v:
Now put it together:
Example: What is
Choose u and v:
- u = ex
- v = x
Differentiate u: (ex)' = ex
Integrate
Now put it together:
Well, that was a spectacular disaster! It just got more complicated.
Maybe we could choose a different u and v?
Example:
Choose u and v differently:
- u = x
- v = ex
Differentiate u: (x)' = 1
Integrate
Now put it together:
Simplify:
x ex − ex + C
ex(x−1) + C
The moral of the story: Choose u and v carefully!
Choose a u that gets simpler when you differentiate it and a v that doesn't get any more complicated when you integrate it.
A helpful rule of thumb is I LATE. Choose u based on which of these comes first:
- I: Inverse trigonometric functions such as sin-1(x), cos-1(x), tan-1(x)
- L: Logarithmic functions such as ln(x), log(x)
- A: Algebraic functions such as x2, x3
- T: Trigonometric functions such as sin(x), cos(x), tan (x)
- E: Exponential functions such as ex, 3x
And here is one last (and tricky) example:
Example:
- u = sin(x)
- v = ex
Differentiate u: sin(x)' = cos(x)
Integrate
Now put it together:
Simplify:
Now we have the same integral on both sides (except one is subtracted) ...
... so bring the right hand one over to the left and we get:
Simplify:
Footnote: Where Did "Integration by Parts" Come From?
It is based on the Product Rule for Derivatives:
(uv)' = uv' + u'v
Integrate both sides and rearrange:
Some people prefer that last form, but I like to integrate v' so the left side is simple:
|
124 videos|176 docs
|
FAQs on Integration by parts method, Business Mathematics & Statistics - Business Mathematics and Statistics - B Com
| 1. What is the integration by parts method? |  |
| 2. How does the integration by parts method work? |  |
| 3. When should I use the integration by parts method? |  |
| 4. Can you provide an example of using the integration by parts method? |  |
| 5. Are there any limitations or conditions for using the integration by parts method? |  |





















