Intrinsic and Extrinsic Material | Modern Physics for IIT JAM PDF Download
Intrinsic Material
A perfect semiconductor crystal with no impurities or lattice defects is called an intrinsic semiconductor. In such material there are no charge carriers at 0K , since the valence band is filled with electrons and the conduction band is empty. At higher temperatures electron-hole pairs are generated as valence band electrons are excited thermally across the band gap to the conduction band. These EHPs are the only charge carriers in intrinsic material.
The generation of EHPs can be visualized in a qualitative way by considering the breaking of covalent bonds in the crystal lattice. If one of the Si valence electrons is broken away from its position in the bonding structure such that it becomes free to move about in the lattice, a conduction electron is created and a broken bond (hole) is left behind. The energy required to break the bond is the band gap energy Eg . This model helps in visualizing the physical mechanism of EHP creation, but the energy band mode is more productive for purposes of quantitative calculation. One Important difficulty in the “broken bond” model is that the free electron and the hole seem deceptively localized in the lattice. Actually, the positions of the free electron and the hole are spread out over several lattice spacing and should be considered quantum mechanically by probability distributions.
e- :Electron, h+ :Hole
Figure: Electron-hole pairs in the covalent bonding model of the Si crystal.
Since the electrons and holes are created in pairs, the conduction band electron concentration n (electrons per cm3 ) is equal to the concentration of holes in the valence band p (holes per cm3 ). Each of these intrinsic carrier concentrations is commonly referred to as ni . Thus for intrinsic material n = p = ni.
At a given temperature there is a certain concentration of electron-hole pairs ni . Obviously, if a steady state carrier concentration is maintained, there must be recombination of EHPs at the same rate at which they are generated. Recombination occurs when an electron in the conduction band makes a transition (direct or indirect) to an empty state (hole) in the valence band, thus annihilating the pair. If we denote the generation rate of EHPs as gi , (EHP/cm3 ) and the recombination rate as ri , equilibrium requires that: ri = gi
Each of these rates is temperature dependent. For example, gi(T) increases when the temperature is raised, and a new carrier concentration ni , is established such that the higher recombination rate ri(T) just balances generation. At any temperature, we can predict that the rate of recombination of electrons and holes ri is proportional to the equilibrium concentration of electrons n0 and the concentration of holes p0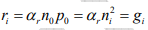
The factor αr is a constant of proportionality which depends on the particular mechanism by which recombination takes place.
Extrinsic Material
In addition to the intrinsic carriers generated thermally, it is possible to create carriers in semiconductor purposely by introducing impurities into the crystal. This process, called doping is the most common technique for varying the conductivity of semiconductors. By doping, a crystal can be altered so that it has a predominance of either electrons or holes. Thus there are two types of doped semiconductors, n-type (mostly electrons) and p-type (mostly holes).
When impurities or lattice defects are introduced into an otherwise perfect crystal, additional levels are created in the energy band structure usually within the band gap. For example, an impurity from column V of the periodic table (P, As, and Sb) introduces an energy level very near the conduction band in Ge or Si. This level is filled with electrons at 0K , and very little thermal energy is required to excite these electrons to the conduction band. Thus at about 50K 100K virtually all of the electrons in the impurity level are “donated” to the conduction band. Such an impurity level is called a donor level and the column V impurities in Ge or Si are called donor impurities. From figure, we note that the material doped with donor impurities can have a considerable concentration of electrons in the conduction band, even when the temperature is too low for the intrinsic EHP concentration to be appreciable. Thus semiconductors doped with a significant number of donor atoms will have n0 >>(ni, p0) at room temperature. This is n-type material.
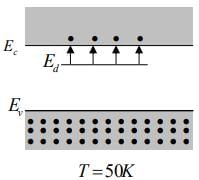
Figure: Donation of electrons from a donor level to the conduction band.
Atoms from column III (B, Al, Ga, and In) introduce impurity levels in Ge or Si near the valence band. These levels are empty of electrons at 0K . At low temperatures, enough thermal energy is available to excite electrons from the valence band into the impurity level, leaving behind holes in the valence band, since this type of impurity level “accepts” electrons from the valence band, it is called an acceptor level, and the column III impurities are acceptor impurities in Ge and Si. Figure below indicates, doping with acceptor impurities can create a semiconductor with a hole concentration p0 much greater than the conduction band electron concentration n0 (this is p- type material).
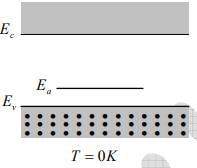
Figure: Acceptance of valence band electrons by an acceptor level, and the resulting creation of holes.
The Fermi Level
Electrons in solids obey Fermi-Dirac statistics. In the development of this type of statistics, one must consider the indistinguishability of the electrons, their wave nature, and the Pauli Exclusion Principle. The rather simple result of these statistical arguments is that the distribution of electrons over a range of allowed energy levels at thermal equilibrium is: 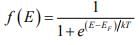
where k is Boltzmann constant. The function f (E) , the Fermi-Dirac distribution function, gives the probability that an available energy state at E will be occupied by an electron at absolute temperature T. The quantity EF is called the Fermi Level, and it represents an important quantity in the analysis of semiconductor behavior. We notice that, for an energy E equal to the Fermi level energy EF , the occupation probability is 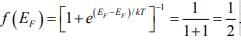
A closer examination of f (E) indicates that at 0K the distribution takes the simple rectangular form shown in figure. With T = 0 in the denominator of the exponent, f(E) is 1/(1 + 0) = 1 when the exponent is negative (E < EF), and is 1/ (1 + ∞) = 0 when the exponent is positive (E > EF). This rectangular distribution implies that at 0K every available energy state up to EF is filled with electrons and all states above EF are empty.
Figure (i): The Fermi Dirac distribution function.
At temperatures higher than 0K , some probability exists for states above EF to be filled. For example, at T = T1 there is some probability f(E) that states above EF are filled, and there is a corresponding probability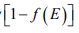 that states below EF are empty.
that states below EF are empty.
The Fermi function is symmetrical about EF for all temperatures; that is the probability 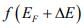 that a state ΔE above EF is filled is the same as the probability
that a state ΔE above EF is filled is the same as the probability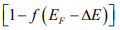 that a state ∆E below EF is empty. The symmetry of the distribution of empty and filled states about EF makes the Fermi level a natural reference point in calculations of electron and hole concentrations in semiconductors.
that a state ∆E below EF is empty. The symmetry of the distribution of empty and filled states about EF makes the Fermi level a natural reference point in calculations of electron and hole concentrations in semiconductors.
For intrinsic material we know that the concentration of holes in the valence band is equal to the concentration of electrons in the conduction band. Therefore, the Fermi level EF must lie at the middle of the band gap in intrinsic material [Figure ii (a)]. Since f(E) is symmetrical about EF , the electron probability "tail" of f(E) extending into the conduction band is symmetrical with the hole probability tail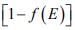 in the valence band. The distribution function has values within the band gap between Ec and Ev but there are no energy states available, and no electron occupancy results from f(E) in this range.
in the valence band. The distribution function has values within the band gap between Ec and Ev but there are no energy states available, and no electron occupancy results from f(E) in this range.
In n-type material there is a high concentration of electrons in the conduction band compared with the hole concentration in the valence band. Thus in n-type material the distribution function f(E) must lie above its intrinsic position on the energy scale [figure ii (b)].
Since f(E) retains its shape for a particular temperature, the larger concentration of electrons at Ec in n-type material implies a correspondingly smaller hole concentration at Ev . We notice that the value of f(E) for each energy level in the conduction band (and therefore the total electron concentration n0 ) increases as EF moves closer to Ec . Thus the energy difference (Ec - EF) gives a measure of n.
For p-type material the Fermi level lies near the valence band [figure ii (c)] such that the 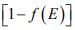 tail below Ev is larger than the f(E) tail above Ec . The value of (EF - Ev) indicates how strongly p-type the material is. It is usually inconvenient to draw f(E) vs E on every energy band diagram to indicate the electron and hole distributions. Therefore, it is common practice merely to indicate the position of EF in band diagrams.
tail below Ev is larger than the f(E) tail above Ec . The value of (EF - Ev) indicates how strongly p-type the material is. It is usually inconvenient to draw f(E) vs E on every energy band diagram to indicate the electron and hole distributions. Therefore, it is common practice merely to indicate the position of EF in band diagrams.
Figure (ii) : The Fermi distribution function applied to semiconductors:
(a) Intrinsic material; (b) n-type material; (c) p-type material.
Temperature Dependence of Carrier Concentrations
The variation of carrier concentration with temperature is indicated by equations 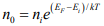 and
and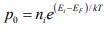 Initially, the variation of no and po with T seems relatively straightforward in these relations. The problem is complicated, however, by the fact that ni has strong temperature dependence
Initially, the variation of no and po with T seems relatively straightforward in these relations. The problem is complicated, however, by the fact that ni has strong temperature dependence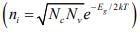 and that EF can also vary with temperature. Let us begin by examining the intrinsic carrier concentration.
and that EF can also vary with temperature. Let us begin by examining the intrinsic carrier concentration. The exponential temperature dependence dominates ni(T) and a plot of ln (ni) vs 1000/T appears almost linear, as shown in figure.
The exponential temperature dependence dominates ni(T) and a plot of ln (ni) vs 1000/T appears almost linear, as shown in figure.
Figure: Intrinsic carrier concentration for Ge, Si, and GaAs as a function of inverse temperature. The room temperature values are marked for reference.
Compensation and Space Charge Neutrality
Figure below illustrates a semiconductor for which both donors and acceptors are present, but ND > NA. The predominance of donors makes the material n-type and the Fermi level is therefore in the upper part of the band gap. Since EF is well above the acceptor level Ea , this level is essentially filled with electrons. However, with EF above Ei we cannot expect a hole concentration in the valence band commensurate with the acceptor concentration. In fact, the filling of the Ea states occurs at the expense of the donated conduction band electrons.
The mechanism can be visualized as follows: Assume an acceptor state is filled with a valence band electron, with a hole resulting in the valence band. This hole is then filled by recombination with one of the conduction band electrons. Extending this logic to all the acceptor atoms, we expect the resultant concentration of electrons in the conduction band to be ND - NA instead of the total ND . This process is called compensation. By this process it is possible to begin with an n-type semiconductor and add acceptors until NA = ND and no donated electrons remain in the conduction band. In such compensated material no = ni = po and intrinsic conduction is obtained. With further acceptor doping the semiconductor becomes p-type with a hole concentration of NA - ND.
Figure: Compensation in an n-type semiconductor (ND - NA).
The exact relationship among the electron, hole, donor, and acceptor concentrations can be obtained by considering the requirements for space charge neutrality. If the material is to remain electrostatically neutral, the sum of the positive charges (holes and ionized donor atoms) must balance the sum of the negative charges (electrons and ionized acceptor atoms): 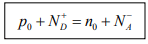
Thus the net electron concentration in the conduction band is 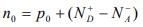 .If the material is doped n-type (n0 >> po) and all the impurities are ionized, we can approximate that no = ND - NA .
.If the material is doped n-type (n0 >> po) and all the impurities are ionized, we can approximate that no = ND - NA .
Since the intrinsic semiconductor itself is electrostatically neutral and the doping atoms we add are also neutral, the requirement of equation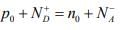 must be maintained at equilibrium.
must be maintained at equilibrium.
Knowledge of carrier concentrations in a solid is necessary for calculating current flow in the presence of electric or magnetic fields. In addition to the values of n and p, we must be able to take into account the collisions of the charge carriers with the lattice and with the impurities. These processes will affect the ease with which electrons and holes can flow through the crystal, that is, their mobility within the solid. As should be expected, these collision and scattering processes depend on temperature, which affects the thermal motion of the lattice atoms and the velocity of the carriers.
|
52 videos|44 docs|15 tests
|
FAQs on Intrinsic and Extrinsic Material - Modern Physics for IIT JAM
| 1. What is the difference between intrinsic and extrinsic material? |  |
| 2. How does intrinsic material affect the properties of a material? |  |
| 3. What are some examples of intrinsic material in everyday objects? |  |
| 4. Can extrinsic material alter the properties of a substance? |  |
| 5. How do intrinsic and extrinsic materials relate to manufacturing processes? |  |





















