Introduction, Laplace Transforms | Calculus - Mathematics PDF Download
The Definition
You know, it’s always a little scary when we devote a whole section just to the definition of something. Laplace transforms (or just transforms) can seem scary when we first start looking at them. However, as we will see, they aren’t as bad as they may appear at first.
Before we start with the definition of the Laplace transform we need to get another definition out of the way.
A function is called piecewise continuous on an interval if the interval can be broken into a finite number of subintervals on which the function is continuous on each open subinterval (i.e. the subinterval without its endpoints) and has a finite limit at the endpoints of each subinterval. Below is a sketch of a piecewise continuous function.
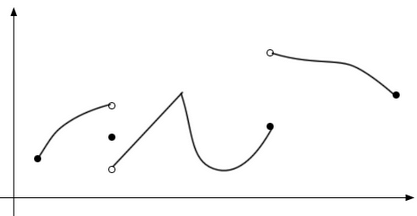
In other words, a piecewise continuous function is a function that has a finite number of breaks in it and doesn’t blow up to infinity anywhere.
Now, let’s take a look at the definition of the Laplace transform.
Definition
Suppose that f(t) is a piecewise continuous function. The Laplace transform of f(t) is denoted L{f(t)} and defined as
 (1)
(1)
There is an alternate notation for Laplace transforms. For the sake of convenience we will often denote Laplace transforms as,
L{f(t)}=F(s)
With this alternate notation, note that the transform is really a function of a new variable,s, and that all the t’s will drop out in the integration process.
Now, the integral in the definition of the transform is called an improper integral and it would probably be best to recall how these kinds of integrals work before we actually jump into computing some transforms.
Example 1 If c≠0, evaluate the following integral.
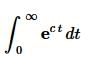
Solution:
Remember that you need to convert improper integrals to limits as follows,
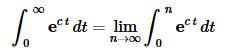
Now, do the integral, then evaluate the limit.
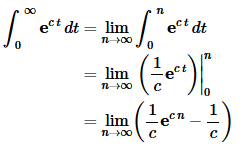
Now, at this point, we’ve got to be careful. The value of c will affect our answer. We’ve already assumed that c was non-zero, now we need to worry about the sign of c. If c is positive the exponential will go to infinity. On the other hand, if c is negative the exponential will go to zero.
So, the integral is only convergent (i.e. the limit exists and is finite) provided c<0. In this case we get,
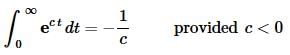 (2)
(2)
Now that we remember how to do these, let’s compute some Laplace transforms. We’ll start off with probably the simplest Laplace transform to compute.
Example 2 Compute L{1}.
There’s not really a whole lot do here other than plug the function f(t)=1 into (1)
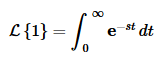
Now, at this point notice that this is nothing more than the integral in the previous example with c=−s. Therefore, all we need to do is reuse (2) with the appropriate substitution. Doing this gives,
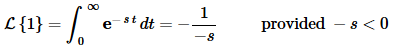
Or, with some simplification we have,

Notice that we had to put a restriction on s in order to actually compute the transform. All Laplace transforms will have restrictions on s. At this stage of the game, this restriction is something that we tend to ignore, but we really shouldn’t ever forget that it’s there.
Let’s do another example.
Example 3 Compute L{eat}
Solution:
Plug the function into the definition of the transform and do a little simplification.
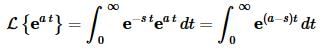
Once again, notice that we can use (2) provided c=a−s. So, let’s do this.
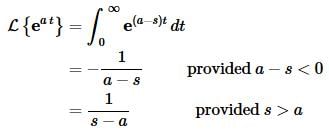
Let’s do one more example that doesn’t come down to an application of (2).
Example 4 Compute L{sin(at)}.
Solution:
Note that we’re going to leave it to you to check most of the integration here. Plug the function into the definition. This time let’s also use the alternate notation.
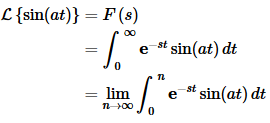
Now, if we integrate by parts we will arrive at,
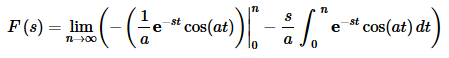
Now, evaluate the first term to simplify it a little and integrate by parts again on the integral. Doing this arrives at,
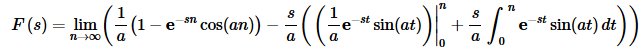
Now, evaluate the second term, take the limit and simplify.

Now, notice that in the limits we had to assume that s>0 in order to do the following two limits.
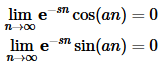
Without this assumption, we get a divergent integral again. Also, note that when we got back to the integral we just converted the upper limit back to infinity. The reason for this is that, if you think about it, this integral is nothing more than the integral that we started with. Therefore, we now get,
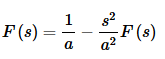
Now, simply solve for F(s) to get,
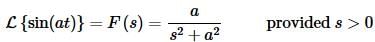
As this example shows, computing Laplace transforms is often messy.
Before moving on to the next section, we need to do a little side note. On occasion you will see the following as the definition of the Laplace transform.
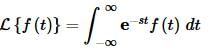
Note the change in the lower limit from zero to negative infinity. In these cases there is almost always the assumption that the function f(t) is in fact defined as follows,

In other words, it is assumed that the function is zero if t<0. In this case the first half of the integral will drop out since the function is zero and we will get back to the definition given in . A Heaviside function is usually used to make the function zero for t<0. We will be looking at these in a later section.
Laplace Transforms
As we saw in the last section computing Laplace transforms directly can be fairly complicated. Usually we just use a table of transforms when actually computing Laplace transforms. The table that is provided here is not an all-inclusive table but does include most of the commonly used Laplace transforms and most of the commonly needed formulas pertaining to Laplace transforms.
Before doing a couple of examples to illustrate the use of the table let’s get a quick fact out of the way.
Fact
Given f(t) and g(t) then,
L{af(t)+bg(t)}=aF(s)+bG(s)
for any constants a and b.
In other words, we don’t worry about constants and we don’t worry about sums or differences of functions in taking Laplace transforms. All that we need to do is take the transform of the individual functions, then put any constants back in and add or subtract the results back up.
So, let’s do a couple of quick examples.
Example 1 Find the Laplace transforms of the given functions.
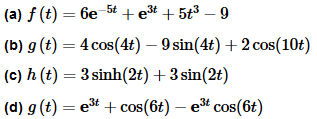
Solution:
Okay, there’s not really a whole lot to do here other than go to the table, transform the individual functions up, put any constants back in and then add or subtract the results.
We’ll do these examples in a little more detail than is typically used since this is the first time we’re using the tables.
(a) f(t)=6e−5t+e3t+5t3−9
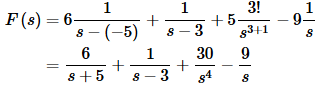
(b) g(t)=4cos(4t)−9sin(4t)+2cos(10t)
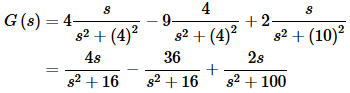
(c) h(t)=3sinh(2t)+3sin(2t)
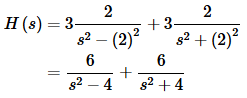
(d) g(t)=e3t+cos(6t)−e3tcos(6t)

Make sure that you pay attention to the difference between a “normal” trig function and hyperbolic functions. The only difference between them is the “+a2” for the “normal” trig functions becomes a “−a2” in the hyperbolic function! It’s very easy to get in a hurry and not pay attention and grab the wrong formula. If you don’t recall the definition of the hyperbolic functions see the notes for the table.
Let’s do one final set of examples.
Example 2 Find the transform of each of the following functions.

Solution:
(a) f(t)=t cosh(3t)
This function is not in the table of Laplace transforms. However, we can use #30 in the table to compute its transform. This will correspond to #30 if we take n=1.
F(s)=L{tg(t)}=−G′(s), where g(t)=cosh(3t)
So, we then have,
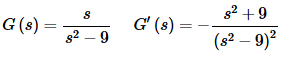
Using #30 we then have,
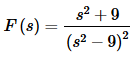
(b) h(t)=t2sin(2t)
This part will also use #30 in the table. In fact, we could use #30 in one of two ways. We could use it with n=1.
H(s)=L{tf(t)}=−F′(s), where f(t)=tsin(2t)
Or we could use it with n=2.
H(s)=L{t2f(t)}=F′′(s), where f(t)=sin(2t)
Since it’s less work to do one derivative, let’s do it the first way. So, using #9 we have,
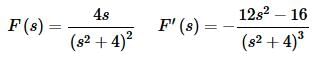
The transform is then,
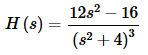
(c) g(t) 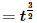
This part can be done using either #6 (with n=2) or #32 (along with #5). We will use #32 so we can see an example of this. In order to use #32 we’ll need to notice that
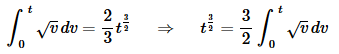
Now, using #5,
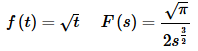
we get the following.
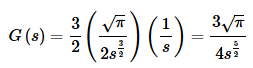
This is what we would have gotten had we used #6.
(d) f(t)=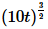
For this part we will use #24 along with the answer from the previous part. To see this note that if
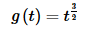
then
f(t)=g(10t)
Therefore, the transform is.
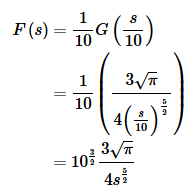
(e) f(t)=tg′(t)
This final part will again use #30 from the table as well as #35.
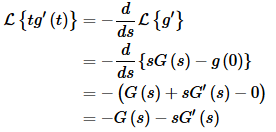
Remember that g(0) is just a constant so when we differentiate it we will get zero!
As this set of examples has shown us we can’t forget to use some of the general formulas in the table to derive new Laplace transforms for functions that aren’t explicitly listed in the table!
Inverse Laplace Transforms
Finding the Laplace transform of a function is not terribly difficult if we’ve got a table of transforms in front of us to use as we saw in the last section. What we would like to do now is go the other way.
We are going to be given a transform, F(s), and ask what function (or functions) did we have originally. As you will see this can be a more complicated and lengthy process than taking transforms. In these cases we say that we are finding the Inverse Laplace Transform of F(s) and use the following notation.
f(t)=L−1{F(s)}
As with Laplace transforms, we’ve got the following fact to help us take the inverse transform.
Fact
Given the two Laplace transforms F(s) and G(s)then
L−1{aF(s)+bG(s)}=aL−1{F(s)}+bL−1{G(s)}
for any constants a and b.
So, we take the inverse transform of the individual transforms, put any constants back in and then add or subtract the results back up.
Let’s take a look at a couple of fairly simple inverse transforms.
Example 1 Find the inverse transform of each of the following.
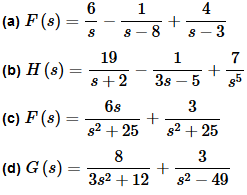
Solution:
We’ve always felt that the key to doing inverse transforms is to look at the denominator and try to identify what you’ve got based on that. If there is only one entry in the table that has that particular denominator, the next step is to make sure the numerator is correctly set up for the inverse transform process. If it isn’t, correct it (this is always easy to do) and then take the inverse transform.
If there is more than one entry in the table that has a particular denominator, then the numerators of each will be different, so go up to the numerator and see which one you’ve got. If you need to correct the numerator to get it into the correct form and then take the inverse transform.
So, with this advice in mind let’s see if we can take some inverse transforms.
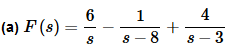
From the denominator of the first term it looks like the first term is just a constant. The correct numerator for this term is a “1” so we’ll just factor the 6 out before taking the inverse transform. The second term appears to be an exponential with a=8 and the numerator is exactly what it needs to be. The third term also appears to be an exponential, only this time a=3 and we’ll need to factor the 4 out before taking the inverse transforms.
So, with a little more detail than we’ll usually put into these,
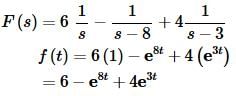

The first term in this case looks like an exponential with a=−2 and we’ll need to factor out the 19. Be careful with negative signs in these problems, it’s very easy to lose track of them.
The second term almost looks like an exponential, except that it’s got a 3s instead of just an s in the denominator. It is an exponential, but in this case, we’ll need to factor a 3 out of the denominator before taking the inverse transform.
The denominator of the third term appears to be #3 in the table with n=4. The numerator however, is not correct for this. There is currently a 7 in the numerator and we need a 4!=24 in the numerator. This is very easy to fix. Whenever a numerator is off by a multiplicative constant, as in this case, all we need to do is put the constant that we need in the numerator. We will just need to remember to take it back out by dividing by the same constant.
So, let’s first rewrite the transform.
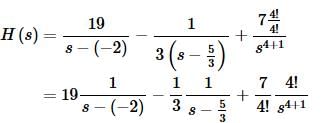
So, what did we do here? We factored the 19 out of the first term. We factored the 3 out of the denominator of the second term since it can’t be there for the inverse transform and in the third term we factored everything out of the numerator except the 4! since that is the portion that we need in the numerator for the inverse transform process.
Let’s now take the inverse transform.
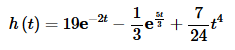
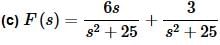
In this part we’ve got the same denominator in both terms and our table tells us that we’ve either got #7 or #8. The numerators will tell us which we’ve actually got. The first one has an s in the numerator and so this means that the first term must be #8 and we’ll need to factor the 6 out of the numerator in this case. The second term has only a constant in the numerator and so this term must be #7, however, in order for this to be exactly #7 we’ll need to multiply/divide a 5 in the numerator to get it correct for the table.
The transform becomes,
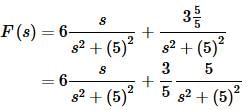
Taking the inverse transform gives,
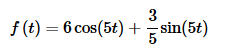
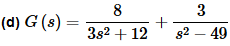
In this case the first term will be a sine once we factor a 3 out of the denominator, while the second term appears to be a hyperbolic sine (#17). Again, be careful with the difference between these two. Both of the terms will also need to have their numerators fixed up. Here is the transform once we’re done rewriting it.
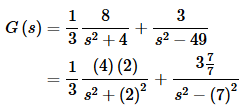
Notice that in the first term we took advantage of the fact that we could get the 2 in the numerator that we needed by factoring the 8. The inverse transform is then,
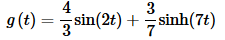
So, probably the best way to identify the transform is by looking at the denominator. If there is more than one possibility use the numerator to identify the correct one. Fix up the numerator if needed to get it into the form needed for the inverse transform process. Finally, take the inverse transform.
Let’s do some slightly harder problems. These are a little more involved than the first set.
Example 2 Find the inverse transform of each of the following.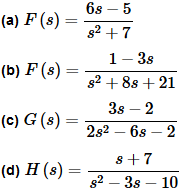
Solution: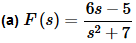
From the denominator of this one it appears that it is either a sine or a cosine. However, the numerator doesn’t match up to either of these in the table. A cosine wants just an s in the numerator with at most a multiplicative constant, while a sine wants only a constant and no s in the numerator.
We’ve got both in the numerator. This is easy to fix however. We will just split up the transform into two terms and then do inverse transforms.
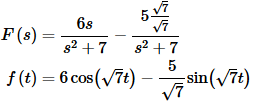
Do not get too used to always getting the perfect squares in sines and cosines that we saw in the first set of examples. More often than not (at least in my class) they won’t be perfect squares!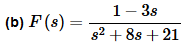
In this case there are no denominators in our table that look like this. We can however make the denominator look like one of the denominators in the table by completing the square on the denominator. So, let’s do that first.
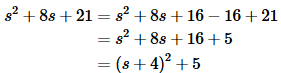
Recall that in completing the square you take half the coefficient of the s, square this, and then add and subtract the result to the polynomial. After doing this the first three terms should factor as a perfect square.
So, the transform can be written as the following.
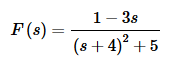
Okay, with this rewrite it looks like we’ve got #19 and/or #20’s from our table of transforms. However, note that in order for it to be a #19 we want just a constant in the numerator and in order to be a #20 we need an s–a in the numerator. We’ve got neither of these, so we’ll have to correct the numerator to get it into proper form.
In correcting the numerator always get the s–a first. This is the important part. We will also need to be careful of the 3 that sits in front of the s. One way to take care of this is to break the term into two pieces, factor the 3 out of the second and then fix up the numerator of this term. This will work; however, it will put three terms into our answer and there are really only two terms.
So, we will leave the transform as a single term and correct it as follows,
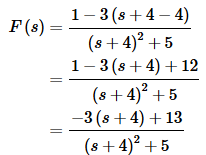
We needed an s+4 in the numerator, so we put that in. We just needed to make sure and take the 4 back out by subtracting it back out. Also, because of the 3 multiplying the s we needed to do all this inside a set of parenthesis. Then we partially multiplied the 3 through the second term and combined the constants. With the transform in this form, we can break it up into two transforms each of which are in the tables and so we can do inverse transforms on them,

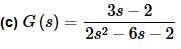
This one is similar to the last one. We just need to be careful with the completing the square however. The first thing that we should do is factor a 2 out of the denominator, then complete the square. Remember that when completing the square a coefficient of 1 on the s2 term is needed! So, here’s the work for this transform.
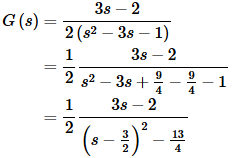
So, it looks like we’ve got #21 and #22 with a corrected numerator. Here’s the work for that and the inverse transform.
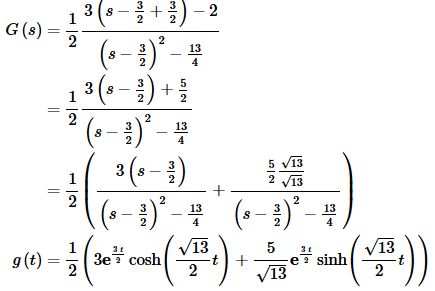
In correcting the numerator of the second term, notice that I only put in the square root since we already had the “over 2” part of the fraction that we needed in the numerator.
This one appears to be similar to the previous two, but it actually isn’t. The denominators in the previous two couldn’t be easily factored. In this case the denominator does factor and so we need to deal with it differently. Here is the transform with the factored denominator.
The denominator of this transform seems to suggest that we’ve got a couple of exponentials, however in order to be exponentials there can only be a single term in the denominator and no s’s in the numerator.
To fix this we will need to do partial fractions on this transform. In this case the partial fraction decomposition will be
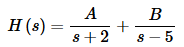
Don’t remember how to do partial fractions? In this example we’ll show you one way of getting the values of the constants and after this example we’ll review how to get the correct form of the partial fraction decomposition.
Okay, so let’s get the constants. There is a method for finding the constants that will always work, however it can lead to more work than is sometimes required. Eventually, we will need that method, however in this case there is an easier way to find the constants.
Regardless of the method used, the first step is to actually add the two terms back up. This gives the following.
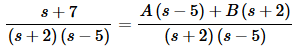
Now, this needs to be true for any s that we should choose to put in. So, since the denominators are the same we just need to get the numerators equal. Therefore, set the numerators equal.
s+7=A(s−5)+B(s+2)
Again, this must be true for ANY value of s that we want to put in. So, let’s take advantage of that. If it must be true for any value of s then it must be true for s=−2, to pick a value at random. In this case we get,
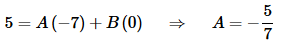
We found A by appropriately picking s. We can B in the same way if we chose s=5.
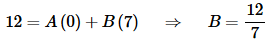
This will not always work, but when it does it will usually simplify the work considerably.
So, with these constants the transform becomes,
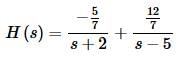
We can now easily do the inverse transform to get,
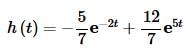
The last part of this example needed partial fractions to get the inverse transform. When we finally get back to differential equations and we start using Laplace transforms to solve them, you will quickly come to understand that partial fractions are a fact of life in these problems. Almost every problem will require partial fractions to one degree or another.
Note that we could have done the last part of this example as we had done the previous two parts. If we had we would have gotten hyperbolic functions. However, recalling the definition of the hyperbolic functions we could have written the result in the form we got from the way we worked our problem. However, most students have a better feel for exponentials than they do for hyperbolic functions and so it’s usually best to just use partial fractions and get the answer in terms of exponentials. It may be a little more work, but it will give a nicer (and easier to work with) form of the answer.
Be warned that in my class I’ve got a rule that if the denominator can be factored with integer coefficients then it must be.
So, let’s remind you how to get the correct partial fraction decomposition. The first step is to factor the denominator as much as possible. Then for each term in the denominator we will use the following table to get a term or terms for our partial fraction decomposition.

Notice that the first and third cases are really special cases of the second and fourth cases respectively.
So, let’s do a couple more examples to remind you how to do partial fractions.
Example 3 Find the inverse transform of each of the following.

Solution: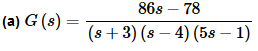
Here’s the partial fraction decomposition for this part.
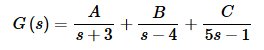
Now, this time we won’t go into quite the detail as we did in the last example. We are after the numerator of the partial fraction decomposition and this is usually easy enough to do in our heads. Therefore, we will go straight to setting numerators equal.
86s−78=A(s−4)(5s−1)+B(s+3)(5s−1)+C(s+3)(s−4)
As with the last example, we can easily get the constants by correctly picking values of s.
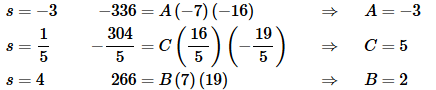
So, the partial fraction decomposition for this transform is,
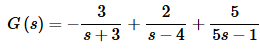
Now, in order to actually take the inverse transform we will need to factor a 5 out of the denominator of the last term. The corrected transform as well as its inverse transform is.
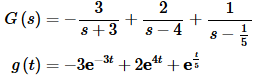
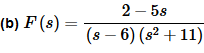
So, for the first time we’ve got a quadratic in the denominator. Here’s the decomposition for this part.
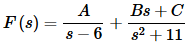
Setting numerators equal gives,
2−5s=A(s2+11)+(Bs+C)(s−6)
Okay, in this case we could use s=6 to quickly find A, but that’s all it would give. In this case we will need to go the “long” way around to getting the constants. Note that this way will always work but is sometimes more work than is required.
The “long” way is to completely multiply out the right side and collect like terms.
2−5s=A(s2+11)+(Bs+C)(s−6)
=As2+11A+Bs2−6B+Cs−6C
=(A+B)s2+(−6B+C)s+11A−6C
In order for these two to be equal the coefficients of the s2, s and the constants must all be equal. So, setting coefficients equal gives the following system of equations that can be solved.
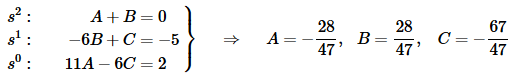
Notice that we used s0 to denote the constants. This is habit on my part and isn’t really required, it’s just what I’m used to doing. Also, the coefficients are fairly messy fractions in this case. Get used to that. They will often be like this when we get back into solving differential equations.
There is a way to make our life a little easier as well with this. Since all of the fractions have a denominator of 47 we’ll factor that out as we plug them back into the decomposition. This will make dealing with them much easier. The partial fraction decomposition is then,
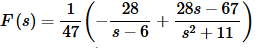
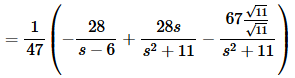
The inverse transform is then.
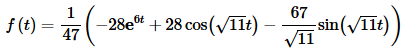
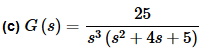
With this last part do not get excited about the s3. We can think of this term as
s3=(s−0)3
and it becomes a linear term to a power. So, the partial fraction decomposition is
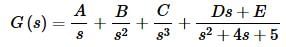
Setting numerators equal and multiplying out gives.
25=As2(s2+4s+5)+Bs(s2+4s+5)+C(s2+4s+5)+(Ds+E)s3
=(A+D)s4+(4A+B+E)s3+(5A+4B+C)s2+(5B+4C)s+5C
Setting coefficients equal gives the following system.
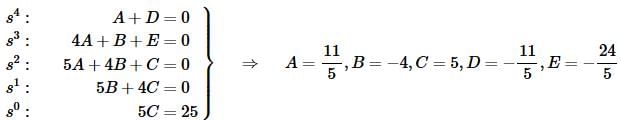
This system looks messy, but it’s easier to solve than it might look. First, we get C for free from the last equation. We can then use the fourth equation to find B. The third equation will then give A, etc.
When plugging into the decomposition we’ll get everything with a denominator of 5, then factor that out as we did in the previous part in order to make things easier to deal with.
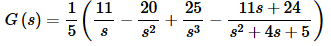
Note that we also factored a minus sign out of the last two terms. To complete this part we’ll need to complete the square on the later term and fix up a couple of numerators. Here’s that work.
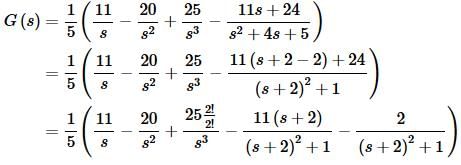
The inverse transform is then.

So, one final time. Partial fractions are a fact of life when using Laplace transforms to solve differential equations. Make sure that you can deal with them.
|
112 videos|65 docs|3 tests
|
FAQs on Introduction, Laplace Transforms - Calculus - Mathematics
| 1. What is the Laplace transform? |  |
| 2. How is the Laplace transform defined? |  |
| 3. What are the advantages of using Laplace transforms in solving differential equations? |  |
| 4. Can Laplace transforms be used for non-linear systems? |  |
| 5. Are there any limitations or drawbacks of using Laplace transforms? |  |

|
Explore Courses for Mathematics exam
|

|

















