Introduction & Concept: Remainder Theorem | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| Concept of Remainder Theorem |

|
| Prime Number Divisor Rule |

|
| Different Types of Questions |

|
| Some Special Cases |

|
Introduction
Supposing a number(or dividend) "D" is divided by another number “d"(divisor); if the quotient obtained is “Q” and the remainder obtained is “R”, then the number can be expressed as D = Q(d) + R.
| Dividend = Quotient(Divisor) + Remainder |
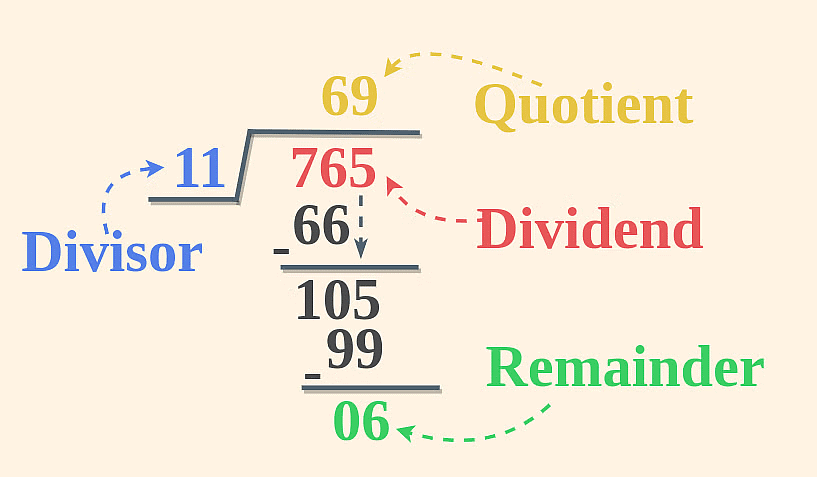
Example: Suppose 8 is divided by 3.
In this case, N = 8, x = 3; 3 × 2 = 6, which is 2 less than 8.
Hence, Q = 2 and R = (8 - 6) = 2
Hence, 8 = 2 × 3 + 2
Concept of Remainder Theorem
The remainder theorem is based on the product of individual remainders. If R is the remainder of an expression (p*q*r)/X, and pR, qR and rR are the remainders when p, q and r are respectively divided by X, then it can be said that ((pR × qR × rR ))/X, will give the same remainder as given by (p*q*r)/X
Let us understand this with the help of an example:
Example 1: Find the remainder when (361*363) is divided by 12.
Ans:
- Take the product of individual remainders, i.e. 361/12 | R =1 and 363/12 | R= 3.
- Find the remainder when you divide that product by the number (361*363)/12 | R= (1*3)/12 | R. => Answer = 3
- This is Basic Remainder theorem put across in Numbers.
Example 2: Find the remainder when 106 is divided by 7, i.e. (106/7)R.
Ans: 106 can be written in the form of 103 x 103
- 106 = 103 x 103
- Thus (106/7)R = (103/7 x 103/7)R = ((6 * 6)/7)R = (36/7)R = 1.
- So the remainder is 1.
➢ Concept of the Negative Remainder
By definition, remainder cannot be negative. But in certain cases, you can assume that for your convenience. But a negative remainder in real sense means that you need to add the divisor in the negative remainder to find the real remainder.
- For example: 15 = 16 × 0 + 15 or 15 = 16 × 1 – 1.
- The remainder when 15 is divided by 16 is 15 the first case and -1 in the second case.
- Hence, the remainder when 15 is divided by 16 is 15 or -1.
- When a number N < D gives a remainder R (= N) when divided by D, it gives a negative remainder of R – D.
Example: When a number gives a remainder of -2 with 23, it means that the number gives a remainder of 23 – 2 = 21 with 23.

- The remainder obtained on the division of a number N by a divisor X can be expressed in two ways as “R” and “X-R”.
Example: 10/11 remainder is +10 itself. It can also be written as 10-11= -1. Similarly, 32/10 remainder is +2 or -8. - Let us express the solution for questions 31 above, in another way- based on the concept of negative remainder. Thus (106/7)R = (103/7 x 103/7)R = ((-1 * -1)/7)R = (1/7)R = 1.
- Remainder when the product of some numbers is divided by the requisite number is the product of individual remainders of the numbers. This is Basic Remainder theorem put across in words.
Let us see why this happens:
If the numbers N1, N2, N3 give remainders of R1, R2, R3 with quotients Q1, Q2, Q3 when divided by a common divisor D
► N1 = DQ1 + R1 N2 = DQ2 + R2 N3 =DQ3 + R3
► Multiplying = N1 * N2 * N3
= (DQ1 + R1) * (DQ2 + R2) * (DQ3 + R3) = D(some number) + (R1 * R2 * R3)
= First part is divisible by D
Hence, you need to check for the individual remainders only.
Prime Number Divisor Rule
The "prime number divisor rule" is a concept related to prime numbers and their divisors. It states that : If P is a prime number, then : The remainder of the expression A(P-1) / P is 1.
Different Types of Questions
Example 1: What is the remainder when the product 1998 × 1999 × 2000 is divided by 7?
Ans: The remainders when 1998, 1999, and 2000 are divided by 7 are 3, 4, and 5 respectively.
- Hence the final remainder is the remainder when the product 3 × 4 × 5 = 60 is divided by 7. Therefore, the remainder = 4
Example 2: What is the remainder when 22004 is divided by 7?
Ans: 22004 is again a product (2 × 2 × 2... (2004 times)).
- Since 2 is a number less than 7, we try to convert the product into the product of numbers higher than 7.
- Notice that 8 = 2 × 2 × 2.
- Therefore we convert the product in the following manner- 22004 = 8668 = 8 × 8 × 8... (668 times).
- The remainder when 8 is divided by 7 is 1.
- Hence the remainder when 8668 is divided by 7 is the remainder obtained when the product 1 * 1 * 1... is divided by 7
Answer = 1
Example 3: What is the remainder when 22006 is divided by 7?
Ans: This problem is like the previous one, except that 2006 is not an exact multiple of 3 so we cannot convert it completely into the form 8x.
- We will write it in the following manner: 22006 = 8668 × 4.
- Now, 8668 gives the remainder 1 when divided by 7 as we have seen in the previous problem.
- And 4 gives a remainder of 4 only when divided by 7.
- Hence the remainder when 22006 is divided by 7 is the remainder when the product 1 × 4 is divided by 7. Therefore, the remainder = 4
Example 4: What is the remainder when 2525 is divided by 9?
Ans: Again 2525 = (18 + 7)25 = (18 + 7)(18 + 7)...25 times = 18K + 725
- Hence remainder, when 2525 is divided by 9, is the remainder when 725 is divided by 9.
- Now 725 = 73 × 73 × 73.. (8 times) × 7 = 343 × 343 × 343... (8 times) × 7.
- The remainder when 343 is divided by 9 is 1, and the remainder when 7 is divided by 9 is 7.
- Hence the remainder when 725 is divided by 9 is the remainder we obtain when the product 1 × 1 × 1... (8 times) × 7 is divided by 9.
- The remainder is 7 in this case. Hence the remainder when 2525 is divided by 9 is 7.
Some Special Cases
➢ When both the dividend and the divisor have a factor in common.
- Let N be a number and Q and R be the quotient and the remainder when N is divided by the divisor D.
Hence, N = Q × D + R. - Let N = k × A and D = k × B where k is the HCF of N and D and k > 1.
Hence kA = Q × kB + R. - Let Q1 and R1 be the quotient and the remainder when A is divided by B.
Hence A = B × Q1 + R1. - Putting the value of A in the previous equation and comparing we get:
k(B × Q1 + R1 ) = Q × kB + R ⇒ R = kR1
Hence to find the remainder when both the dividend and the divisor have a factor in common:
- Take out the common factor (i.e. divide the numbers by the common factor).
- Divide the resulting dividend (A) by resulting divisor (B) and find the remainder (R1 ).
- The real remainder R is this remainder R1 multiplied by the common factor (k).
➢ When a dividend is of the form an + bn or an – bn
Example : What is the remainder when 3444 + 4333 is divided by 5?
Ans: The dividend is in the form ax + by . We need to change it into the form an + bn.
- 3444 + 4333 = (34) 111 + (43) 111.
- Now (34) 111 + (43) 111 will be divisible by 34 + 43 = 81 + 64 = 145.
- Since the number is divisible by 145, it will certainly be divisible by 5.
Hence, the remainder is 0.
➢ When f(x) = a + bx + cx2 + dx3 +… is divided by x – a
Example: Find the remainder when x3 - ax2 + 6x - a is divided by x - a.
Ans: Let p(x) be any polynomial of degree greater than or equal to one and let 'a' be any real number. If a polynomial p(x) is divided by x - a then the remainder is p(a).
Let p(x) = x3 - ax2 + 6x - a
The root of x - a = 0 is a.
p(a) = (a)3 - a(a)2 + 6(a) - a
= a3 - a3 + 5a
= 5a
Hence by remainder theorem, 5a is the remainder when x3 - ax2 + 6x - a is divided by x - a.
Example: If 2x 3 -3x 2 + 4x + c is divisible by x – 1, find the value of c.
Ans: Since the expression is divisible by x – 1, the remainder f(1) should be equal to zero.(by Remainder Theorem)
Or 2 – 3 + 4 + c = 0, or c = -3.
➢ Fermat’s Theorem
If p is a prime and a is a positive integer
a) For a p and any integer a,
ap ≡ a(mod p)
b) Furthermore, if p ∤ a,
then ap−1≡1(mod p)
For example, if a = 2 and p = 7, then 27 = 128, and 128 − 2 = 126 = 7 × 18 is an integer multiple of 7.
Example: What is the remainder when n7 – n is divided by 42?
Ans: Since 7 is prime, n7 – n is divisible by 7.
- n 7 – n = n(n 6 – 1) = n (n + 1)(n – 1)(n 4 + n 2 + 1)
- Now (n – 1)(n)(n + 1) is divisible by 3! = 6
- Hence n 7 – n is divisible by 6 x 7 = 42.
- Hence the remainder is 0.
➢ Wilson’s Theorem
If p is a prime number, then p divides (p−1)!+1.
Example: Find the remainder when 16! Is divided by 17.
Ans: 16! = (16! + 1) -1 = (16! + 1) + 16 – 17
- Every term except 16 is divisible by 17 in the above expression.
- Hence, the remainder = the remainder obtained when 16 is divided by 17 = 16
➢ To Find the Number of Numbers, That Are Less Than or Equal to A Certain Natural Number N, And That Are Divisible by A Certain Integer
- To find the number of numbers, less than or equal to n, and that is divisible by a certain integer p, we divide n by p.
- The quotient of the division gives us the number of numbers divisible by p and less than or equal to n.
Example: How many numbers between 1 and 400, both included, are not divisible either by 3 or 5?
Ans: We first find the numbers that are divisible by 3 or 5. Dividing 400 by 3 and 5, we get the quotients as 133 and 80 respectively.
- Among these numbers divisible by 3 and 5, there are also numbers which are divisible both by 3 and 5, i.e. divisible by 3 x 5 = 15.
- We have counted these numbers twice. Dividing 400 by 15, we get the quotient as 26.
- Hence, the number divisible by 3 or 5 = 133 + 80 – 26 = 187
- Hence, the numbers not divisible by 3 or 5 are = 400 – 187 = 213.
|
174 videos|243 docs|95 tests
|
FAQs on Introduction & Concept: Remainder Theorem - Quantitative Aptitude (Quant) - CAT
| 1. What is the concept of the Remainder Theorem? |  |
| 2. How is the Prime Number Divisor Rule related to the Remainder Theorem? |  |
| 3. What are the different types of questions that can be solved using the Remainder Theorem? |  |
| 4. Are there any special cases to consider when applying the Remainder Theorem? |  |
| 5. How can the Remainder Theorem be applied to solve problems in competitive exams? |  |















