Introduction & Examples: Sets | Quantitative for GMAT PDF Download
| Table of contents |

|
| What is a Set? |

|
| Representation of a Set |

|
| Important Concepts of Sets |

|
| Operations of Sets |

|
| Facts and Rules |

|
| Venn Diagrams |

|
| Maximum and Minimum Elements in a Set |

|
| Solved Examples |

|
What is a Set?
- "Set" is synonymous with the words "collection", "aggregate", "class" and is comprised of
elements/objects/members. - A set is a well-defined collection of elements. By well-defined elements it means
that given a set and an element, it must be possible to decide whether or not the
element belongs to the set. 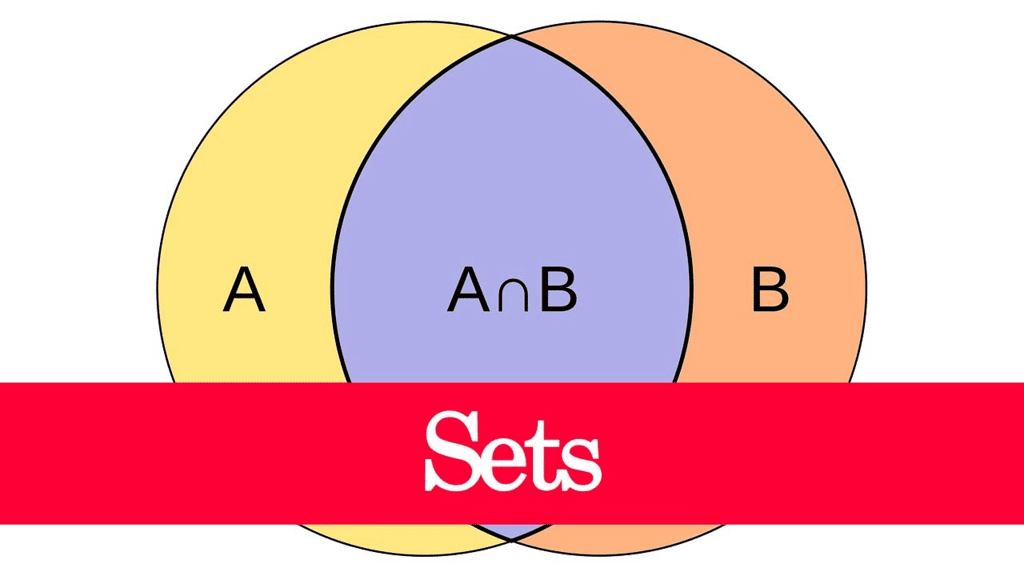 A set can be described in any one of the following ways.
A set can be described in any one of the following ways.
For example, the set of beautiful Actress of Bollywood or the set of Good Players of cricket in India are not sets as the world beautiful and Good are not well defined. What are the criteria of choosing an actress as beautiful and which player is said to be a good player of cricket.
But on the other hand if we say Set of good player of cricket in India who has played at least 25 international games, will be a set as the word Good is now well defined.
Representation of a Set
A set can be described in two different ways1. Roaster Form:
- A set is described by listing elements, separated by commas, within
brackets. - For example, A = {a, e, i, o, u} is a set of vowels of English
alphabets and a finite set and N = {2, 4, 6,…} is a set of even natural
number and is a infinite set. - Also, repetition of an element has no effect.
For example {1, 2, 3, 2} is the same set as {1, 2, 3}.
2. Set Builder Form:
- A set can also be described by a characterizing property P(x) of its
elements x. - In such a case the set is described by {x | P (x) holds} or {x :
P(x) holds}, which is read as 'the set of all x such that P(x) holds'. - For example,
A = {x | x is the root of x2 + 5x - 6 = 0}
Important Tip:
If a set contains a countable number of elements, it is called a finite set and if it contains an uncountable number of elements, it is called an infinite set.
Important Concepts of Sets
1. Cardinal number of a set
- Thenumber of elements contained in a set is known as the cardinal number of that set. On the basis of cardinal number, a set can be an Empty Set or a Singleton Set.
- A set is said to be empty or void or null set if it has no elements and its cardinal number is 0. It is denoted by the symbolφ or {} such as Set of odd numbers divisible by 2.
- A set is singleton set if the cardinal number is 1 i.e. it contains only one element, such as Set of lady Prime-minister of India. If a set A has 5 elements then its cardinal number is written as n(A) = 5, and read as “Cardinal number of set A is 5”.
2. Subsets
- Let A and B be two sets. If every element of A is contained in B, then A is called
the subset of B. - If A is subset of B, we write A ⊂ B,which is read as "A is a subset of B" or "A is
contained in B".
Important Tip:
Let A be a finite set having n elements. Then the total number of subsets of A is 2n and the number of proper subsets of A is 2n - 1.
- If A ⊂ B then a ∈ A ⇒ a ∈ B. (The symbol ⇒ stands for "implies" and ∈ stands for “belongs to”).
- Let P = {a, b, c}, then subsets of P are φ, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} i.e. it has 8 number of
subsets and Empty set is the subset of every. Also every set is the subset of itself and it is improper subset of the set. Every set has one improper subset and other subsets as proper subsets. - If A ⊂ B and also B ⊂ A, then we can say every element of A is present in B and every element of B is
present in A. These types of sets having same number and identical elements are known asEqual sets.
3. Power Set
- The set of subsets of a set is the power set of the set. If A is a set then its Power set is denoted as P(A).
- If A = {a, b, c}, then P(A) = {φ, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}
- The cardinal number of any set A is 2n, where n = number of elements present in set .
4. Universal Set
- In any discussion in theory, there happens to be a set U that contains all sets under consideration., such a set is called the universal set.
- Thus a set that contains all sets in a given context is called the universal set. For example, in plane geometry, the set of all points in the plane is the universal set.
- Some Important Universal Sets:
N = Set of all natural numbers = {1, 2, 3, 4,…}
Z or I Set of all integers ={…- 3, - 2, - 1, 0, 1, 2, 3,..}
Z+ = Set of all positive integers = {1, 2, 3,…} = N
Z- = Set of all negative integers = {- 1, - 2, - 3,..}
W = Set of all whole numbers = {0, 1, 2, 3,…}
Z0 = The set of all non-zero integers = {± 1, ± 2, ± 3,..}
Q = The set of all rational numbers.
R = The set of all real numbers. - R - Q = The set of all irrational numbers.
etc. are all irrational numbers.
Operations of Sets
1. Union of Sets:
- The union of two sets A and B, is a set containing all the elements present in set A or in set B. The union of set A and B is represented as A U B.
- So, AUB = {x | x ∈ A or x ∈ B}
- For example:
A = {5, 7, 8, 9, 11} and B = {car, house, ball, sofa), then
A U B = {5, 7, 8, 9, 11, car, house, ball, sofa}
2. Intersection of Sets:
- The intersection of two sets A and B, is a set containing all the common elements present in set A and in set B. The intersection of set A and B is represented as A ∩ B.
- So, A ∩ B = {x | x ∈ A and x ∈ B}
- For example
A = {5, 7, 8, 9, 11} and B = {3, 4, 5, 6, 7, 8}, then
A ∩ B = {5, 7, 8}
Important Tip:
(a) Two sets are disjoint sets if and only they do not have any common element.
(b) The cardinal number of their intersection is Zero.
3. Difference of sets:
- A - B is the difference of set A from set B and is defined as the set of elements present in set A but not in set B.
- So, A - B = {x | x ∈ A and x ∉ B}
Important Tip:
The difference of two sets is not commutative, i.e., A-B is not equal to B- A.
4. Complement of a set:
- The complement of set A in U the set of those elements which are present in Universal set but not present in set A. Compliment of A is denoted by A' The shaded part represents A'.
- So, A‘= {x | x ∈ U and x ∉ A}
- Also the Compliment of set A is defined as the difference of Universal set U and set A. i.e.⇒ A‘ = U - A
Facts and Rules
i. A ∪ A = A & A ∩ A = A
ii. A ∪ φ = A & A ∩ φ = φ
iii. A ∪ U = U & A ∩ U = A
iv. A ∪ B = B ∪ A & A ∩ B = B ∩ A
v. A ∪ A’ = U & A ∩ A’ = φ
vi. n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
vii. n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - (C ∩ A) + n(A∩B∩C)
viii. n (A - B) = n (A) - n (A ∩ B)
Example:
Q: In a certain city only two newspapers A & B are published. It is known that 25% of the city population reads A & 20% read B while 8% read both A & B. It is also known that 30% of those who read A but not B, look into advertisements and 40% of those who read B but not A, look into advertisements while 50% of those who read both A & B look into advertisements. What % of the population reads an advertisement?
Sol.Let A & B denote sets of people who read paper A & paper B respectively and in all there are 100
people, then n(A) = 25, n(B) = 20, n (A ∩ B) = 8.
Hence the people who read paper A only i.e. n(A - B) = n (A) - n(A ∩ B) = 25 - 8 = 17.
And the people who read paper B only i.e. n(B - A) = n (B) - n (A ∩ B) = 20 - 8 = 12.
Now percentage of people reading an advertisement
= [(30% of 17) + (40% of + 12) + (50% of 8)]% =13.9 %.
Venn Diagrams
Venn diagram is the pictorial representation of the set and also the operation involved in the sets. We often use circles to represent the sets and overlapping of the circles to represent the common elements in two or more sets. The universal set U is represented by the interior of a rectangle and its subsets are represented by the interior of circles within the rectangle. Below are some examples of Venn diagrams.
1. U = universal set
A = subset of U
A’ = complement of A
2. The representation of A U B in Venn diagram is
3. The representation of A ∩ B in Venn diagram is
4. Difference of set A from B i.e. A - B
Maximum and Minimum Elements in a Set
- Let us consider the formula, n(A ∪ B) = n(A) + n(B) - n(A ∩ B) and imagine that the value of n(A ∪ B) is not given and asked to find the value of n(A ∩ B), then we will get the range of the values.
- Let us understand the concept of maximum and minimum values with the help of an example.
Q: In a B - school there are three specializations in Management course and a student is free to specialize in any number of fields. These specializations are Finance, Marketing and HRD. If 120 students specialize in Finance, 110 in Marketing and 125 are in HRD. 90 students have finance and Marketing both as their specialization, 85 have marketing and HRD while 80 have both finance and HRD. What can be the minimum and maximum number of students who can specialization in all the three fields?
Sol. Let us consider that the number of student who enroll in all the three streams be x. Thus according to the Venn diagram drawn with the help of given information.
Now for the minimum value of x, we have x - 65 ≥ 0 ⇒ x ≥ 65
And for maximum value of x, we have 80 - x ≥ 0 ⇒ x ≤ 80
Hence 65 ≤ x ≤ 80.So we have the range of the values that can be the required solution.
Q: If in a Survey, Organized by any N.G.O on the cold drinks after effects found that 80% of the total people like Coca - Cola and 70% like Limca. What can be the minimum and maximum number of people who drink both the drinks?
Sol.
Here n(L ∪ C) ≤ 100%
Using the formula, n(L) + n(C) - n(L ∩ C) = n(L ∪ C) ≤ 100%
80 + 70 - X ≤ 100
Solving we get X ≥ 50%, Also X ≤ 70%
Minimum value = 50% and Maximum value = 70%.
Solved Examples
Example 1:In a class 40% of the students enrolled for Math and 70% enrolled for Economics. If 15% of the students enrolled for both Math and Economics, what % of the students of the class did not enroll for either of the two subjects?
(a) 5%
(b) 15%
(c) 0%
(d) 25%
(e) None of these
Ans: (a)
Explanation:Let A be the set of students who enrolled for Math.
Let B be the set of students who enrolled for Economics.
(A ∪ B) is the set of students who have enrolled for at least one of the two subjects.
And (A ∩ B) is the set of students who have enrolled for both Math and Economics.
n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
In this question, all n(A), n(B), n(A ∪ B), and (A ∩ B) are expressed in percentage terms.
n(A ∪ B) = 40 + 70 - 15 = 95%
That is 95% of the students have enrolled for at least one of the two subjects Math or Economics.
Therefore, the balance (100 - 95)% = 5% of the students have not enrolled for either of the two subjects.
Choice A is the correct answer.
Example 2: In a class of 40 students, 12 enrolled for both English and German. 22 enrolled for German. If the students of the class enrolled for at least one of the two subjects, then how many students enrolled for only English and not German?
(a) 30
(b) 10
(c) 18
(d) 28
(e) 32
Ans:(c)
Explanation:Let A be the set of students who have enrolled for English and B be the set of students who have enrolled for German.
Then, (A ∪ B) is the set of students who have enrolled for at least one of the two languages.
Because the students of the class have enrolled for at least one of the two languages, we will not find anyone outside A ∪ B in this class.
Therefore, n(A ∪ B) = number of students in the class
So, n(A ∪ B) = 40
n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
i.e., 40 = n(A) + 22 - 12
Or n(A) = 30
n(A) is the number of students who have enrolled for English.
This number is the sum of those who have enrolled for only English and those who have enrolled for both the languages.
What we have to compute the number of students who have enrolled for only English.
n(only English)= n(English) - n(A ∩ B)
= 30 - 12 = 18.
Choice C is the correct answer.
Example 3: Of the 200 candidates who were interviewed for a position at a call center, 100 had a two-wheeler, 70 had a credit card and 140 had a mobile phone. 40 of them had both, a two-wheeler and a credit card, 30 had both, a credit card and a mobile phone and 60 had both, a two wheeler and mobile phone and 10 had all three. How many candidates had none of the three?
(a) 0
(b) 20
(c) 10
(d) 18
(e) 25
Ans:(c)
Explanation:Number of candidates who had none of the three = Total number of candidates - number of candidates who had at least one of three.
Total number of candidates = 200.
Number of candidates who had at least one of the three = n(A ∪ B ∪ C),
where A is the set of those who have a two wheeler, B is the set of those who have a credit card, and C is the set of those who have a mobile phone.
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - {n(A ∩ B) + n(B ∩ C) + n(C ∩ A)} + n(A ∩ B ∩ C)
Therefore, n(A ∪ B ∪ C) = 100 + 70 + 140 - {40 + 30 + 60} + 10
Or n(A ∪ B ∪ C) = 190.
n(A ∪ B ∪ C) is the number of candidates who had at least one of three.
As 190 candidates who attended the interview had at least one of the three,
(200 - 190 = 10) candidates had none of three.
Choice C is the correct answer.
Example 4: In a class of 120 students numbered 1 to 120, all even numbered students opt for Physics, those whose numbers are divisible by 5 opt for Chemistry and those whose numbers are divisible by 7 opt for Math. How many opt for none of the three subjects?
(a) 19
(b) 41
(c) 21
(d) 57
(e) 26
Ans: (b)
Explanation:Approach: Let us find the number of students who took at least one of the three subjects and subtract the result from the overall 120 to get the number of students who did not opt for any of the three subjects.
Number of students who took at least one of the three subjects can be found by finding out n(A U B U C), where A is the set of students who took Physics, B is the set of students who took Chemistry and C is the set of students who opted for Math.
Now, n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - {n(A ∩ B) + n(B ∩ C) + n(C ∩ A)} + n(A ∩ B ∩ C)
n(A) is the number of students who opted for Physics = 120/2 = 60
n(B) is the number of students who opted for Chemistry = 120/5 = 24
n(C) is the number of students who opted for Math = 120/7 = 17
Number of students who opted for Physics and Chemistry
Students whose numbers are multiples of 2 and 5 i.e., common multiples of 2 and 5 would have opted for both Physics and Chemistry.
The LCM of 2 and 5 will be the first number that is a multiple of 2 and 5. i.e., 10 is the first number that will be a part of both the series.
The 10th, 20th, 30th..... numbered students or every 10th student starting from student number 10 would have opted for both Physics and Chemistry.
Therefore, n(A ∩ B) = 120/10 = 12
Number of students who opted for Physics and Math
Students whose numbers are multiples of 2 and 7 i.e., common multiples of 2 and 7 would have opted for both Physics and Math.
The LCM of 2 and 7 will be the first number that is a multiple of 2 and 7. i.e., 14 is the first number that will be a part of both the series.
The 14th, 28th, 42nd..... numbered students or every 14th student starting from student number 14 would have opted for Physics and Math.
Therefore, n(C ∩ A) = 120/14 = 8
Number of students who opted for Chemistry and Math
Students whose numbers are multiples of 5 and 7 i.e., common multiples of 5 and 7 would have opted for both Chemistry and Math.
The LCM of 5 and 7 will be the first number that is a multiple of 5 and 7. i.e., 35 is the first number that will be a part of both the series.
The 35th, 70th.... numbered students or every 35th student starting with student number 35 would have opted for Chemistry and Math.
Therefore, n(B ∩ C) = 120/35 = 3
Number of students who opted for all three subjects
Students whose numbers are multiples of 2, 5, and 7 i.e., common multiples of 2, 5, and 7 would have opted for all 3 subjects.
The LCM of 2, 5, and 7 will be the first number that is a multiple of 2, 5, and 7. i.e., 70 is the first number that will be a part of all 3 series.
70 is the only multiple of 70 in the first 120 natural numbers. So, the 70th numbered student is the only one who would have opted for all three subjects.
Therefore, n(A ∪ B ∪ C) = 60 + 24 + 17 - (12 + 8 + 3) + 1 = 79.
n(A ∪ B ∪ C) is the number of students who opted for at least one of the 3 subjects.
Number of students who opted for none of the three subjects = 120 - n(A ∪ B ∪ C)
= 120 - 79 = 41.
Choice B is the correct answer.
|
121 videos|148 docs|111 tests
|
FAQs on Introduction & Examples: Sets - Quantitative for GMAT
| 1. What is a set in mathematics? |  |
| 2. How can sets be represented? |  |
| 3. What are the important concepts related to sets? |  |
| 4. What operations can be performed on sets? |  |
| 5. How are Venn diagrams used in relation to sets? |  |
















