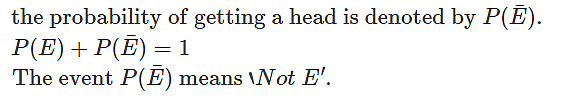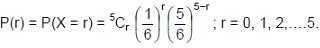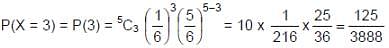Introduction: Probability | Quantitative Aptitude (Quant) - CAT PDF Download

Probability for CAT is an important topic in the CAT quantitative aptitude section. You can expect 2-3 questions from probability in the quant section in CAT. Probability helps us determine the odds of an event happening or not happening.  

What is Probability?

Probability is simply how likely something is to happen. Whenever you’re not certain about the outcome of an event, you can talk about the probabilities of certain outcomes—how likely they are. Probability can range from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event.
For example, when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible (H, T). But when two coins are tossed then there will be four possible outcomes,  i.e {(H, H), (H, T), (T, H), (T, T)}.

Formula for Probability

The probability formula is defined as the possibility of an event to happen is equal to the ratio of the number of favourable outcomes and the total number of outcomes.

Probability of event to happen P(E) = Number of favourable outcomes/Total Number of outcomes

Important Concepts of Probability 

Concept of AND/ OR

Usually you would encounter two major types of problems in Probability with the the use of
conjunctions AND and OR.
In general, event definition means breaking up the event to the most basic building blocks, which are commonly through the two English conjunctions— AND and OR.

• ‘AND’ as a binding conjunctive.
  Whenever you see AND as the natural conjunction joining two separate parts of the event definition, you can replace the AND by the multiplication (X) sign.
  Thus, if E AND R have to occur, and if the probability of their occurrence are P(E) and P(R) respectively, then the probability that E AND R occur is obtained by connecting P(E) AND P(R). Replacing the AND by multiplication sign you get the required probability as:
  Req Probability = P(E) X P(R)
  Example. Let’s try solving an example, If you have the probability of E hitting a target as 1/2 and that of R hitting the target as 1/5, then the probability that both hit the target if one shot is taken by both of them is?
  Sol. Event here is that E hits the target AND R hits the target, both hitting the target. Hence the resulting probability is going to be
  Probability =  P(E) AND P(R) = P(E) X P(R)
  Using the values given of P(E) & P(R),
  P(E) X P(R) = ½  X ⅕  = 1/10
  
  Question for Introduction: Probability

  Try yourself:In a throw of two dice, find the probability of getting one prime and one composite number.

  • A.

    ½
  • B.

    ⅓
  • C.

    ⅔
  • D.

    ¾

  Explanation

  The probability of getting a prime number - 2,3 & 5  when a dice is thrown is 3/6 = 1/2.

  Similarly, in a throw of a dice, there are only 2 possibilities of getting composite numbers viz : 4 or 6 and this gives a probability of 1/3 for getting a composite number.
  The event is— getting one prime and one composite number.
  This can be got as:
  The first number is prime and the second is composite OR the first number is composite and the second is prime.
  = (1/2) X (1/3) + (1/3) X (1/2) = 1/3
  EduRev Tip: ‘1’ is not a prime number.
  ‘OR’ as a binding conjunctive.
  Whenever you use OR as the natural conjunction joining two separate parts of the event definition, you replace the OR by the addition (+) sign.
  Thus, if E OR R have to occur, and if the probability of their occurrence are P(E) and P(R) respectively, then the probability that E OR R occur is obtained by connecting P(E) AND P(R). Replacing the OR by addition sign you get the required probability as:
  Req Probability = P(E) + P(R)

  Report a problem

  Cancel Report

  View Solution
• 'OR’ as a binding conjunctive 
  Whenever you see OR as the natural conjunction joining two separate parts of the event definition, you can replace the OR with the addition (+) sign.
  Thus, if E OR R have to occur, and if the probability of their occurrence is P(E) and P(R) respectively, then the probability that E OR R occurs is obtained by connecting P(E) OR P(R) i.e. replacing the OR by addition sign you get the required probability as:
  Example. If you have the probability of E hitting a target as 1/2 and that of R hitting the target as 1/5, then the probability that both hit the target if one shot is taken by either of them is?
  Sol. As you can see whether E OR R hits the target, the outcome is counted even if one of them hits the target. Hence the resulting probability is going to be
  Probability =  P(E) OR P(R) = P(E) + P(R)
  Using the values given of P(E) & P(R),
  P(E) + P(R) = ½ + ⅕  = 7/10
  Unlike above example where the event will happen only with both E & R events occurring , here if any one of E, R events can occur.
• Combination of ‘AND’ and ‘OR’
  You would encounter  where in once the event is defined, the probability of each sub event within the broad event is calculated and all the sub events are connected by Multiplication (for AND) or by Addition (for OR) to get the final solution.
  Example. If two dice are thrown, what is the chance that the sum of the numbers is not less than 10.
  Sol. Event Definition- The sum of the numbers is not less than 10 if it is either 10 OR 11 OR 12.
  Which can be done by
  P(E) = (6 AND 4) OR (4 AND 6) OR (5 AND 5) OR (6 AND 5) OR (5 AND 6) OR (6 AND 6) that is, ⅙ X ⅙  + ⅙ X ⅙  + ⅙ X ⅙  + ⅙ X ⅙  + ⅙ X ⅙  + ⅙ X ⅙   =  6/36  = ⅙
  Hence for the event of sum less than 10, P(E’) = 1 - P(E) = 1 - ⅙ = ⅚ .
  can see that no matter how many broad & sub events the problem of probability is, it can be broken up into its narrower parts, which can be connected by ANDs and ORs to get the event definition.
  
  Question for Introduction: Probability

  Try yourself:In a four game match between Monica and Chandler, the probability that Chandler wins a particular game is 2/5 and that of Monica winning a game is 3/5. Assuming that there is no probability of a draw in an individual game, what is the chance that the match is drawn (Score is 2–2).

  • A.

    213/625
  • B.

    211/625
  • C.

    216/625
  • D.

    ¼

  Explanation

  For the match to be drawn, 2 games have to be won by each of the players. If ‘A’ represents the event that Monica won a game and K represents the event that Chandler won a game, the event definition for the match to end in a draw can be described as: [The student is advised to look at the use of sub event definition.]
  (M & M & C& C) OR (M&C&C&K) OR (M&C&C&M) OR (C&C&M&M) OR (C&M&C&M) OR (C&M&M&C)
  This further translates into
  (⅖)X(⅖)X(⅗) X (⅗) + (⅖)X(⅖)X(⅗) X (⅗) + (⅖)X(⅖)X(⅗) X (⅗) + (⅖)X(⅖)X(⅗) X (⅗) + (⅖)X(⅖)X(⅗) X (⅗)    = (36/625) X 6
  = 216/625

  EduRev Tip:  In the above question you tried to identify the sub-events & try to add them based on the event definition.

  Report a problem

  Cancel Report

  View Solution

1. Conditional Probability 

• The conditional probability, as its name suggests, is the probability of happening an event that is based upon a condition. 
• For example, assume that the probability of a boy playing tennis in the evening is 95% (0.95) whereas the probability that he plays given that it is a rainy day is less which is 10% (0.1). Then the former case is just normal probability whereas the latter case is the conditional probability. In this example, we represent the two probabilities as P(Play tennis) = 0.95 and P(Play tennis | Rainy day) = 0.1. 
• The conditional probability of event A given that B has occurred is given by P(A/B) = P( A ∩ B)/ P (B), provided P(B) ≠ 0. 
  

Here:

• P(A | B) = The probability of A given B (or) the probability of A which happens after B
• P(B | A) = The probability of B given A (or) the probability of B which happens after A
• P(A ∩ B) = The probability of happening of both A and B
• P(A) = The probability of A
• P(B) = The probability of B
  
  

2. Baye's Theorem

• Bayes’ theorem describes the probability of occurrence of an event related to any condition. It is also considered for the case of conditional probability.
  
• Example
  A man is known to speak the truth 2 out of 3 times. He throws a die and reports that the number obtained is a four. Find the probability that the number obtained is actually a four.
  Solution:
  Let A be the event that the man reports that number four is obtained.
  Let E₁ be the event that four is obtained and E₂ be its complementary event.
  Then, P(E₁) = Probability that four occurs = 1/6.
  P(E₂) = Probability that four does not occur = 1- P(E₁) = 1 – (1/6) = 5/6.
  Also, P(A|E₁)= Probability that man reports four and it is actually a four = 2/3
  P(A|E₂) = Probability that man reports four and it is not a four = 1/3.
  By using Bayes’ theorem, probability that number obtained is actually a four, P(E₁|A)

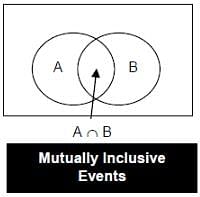
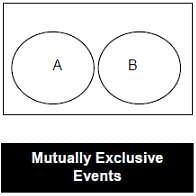
3. Mutually Exclusive Events

• Two or more events are said to be mutually exclusive; these events cannot occur simultaneously. Two or more events are said to be compatible if they can occur simultaneously. 
• Two events (A and B) are mutually exclusive if the intersection of two events is null or they have no common element i.e. A ∩ B = φ.
  e.g. In drawing a card from a deck of 52 cards:
  A: The event that it is red.
  B: The event that it is black.
  C: The event that it is a king.
  In the above case events A and B are mutually exclusive but the events B and C are not mutually exclusive or disjoint since they may have common outcomes.
   
  

4. Equally likely events: 

• If two events have the same probability or chance of occurrence they are called equally likely events. (In a throw of a dice, the chance of 1 showing on the dice is equal to 2 is equal to 3 is equal to 4 is equal to 5 is equal to 6 appearing on the dice.)

5. Exhaustive set of events: 

• A set of events that includes all the possibilities of the sample space is said to be an exhaus- tive set of events. (e.g. In a throw of a dice the number is less than three or more than or equal to three.)

6. Independent events:

•  An event is described as such if the occurrence of an event has no effect on the probability of t76he occurrence of another event. (If the first child of a couple is a boy, there is no effect on the chances of the second child being a boy.)

7. Random Experiment: 

• It is the one which gives one or more results under identical conditions. E.g. a coin is tossed.
  The set of all possible outcomes of a random experiment is known as the sample space and every outcome is a sample point.
• Example. A coin is tossed and a single 6-sided dice is rolled. Find the probability of getting ahead on the coin and a 3 on the dice.
  Sol. P(head) = 1/2
  P(3) = 1/6
  P(head and 3) = 1/2.1/6 = 1/12

8. Sum Rule

• If E and F are two mutually exclusive events, then the probability that either event E or event F will occur in a single trial is given by:
• P(E or F) or P (E ∪ F) = P(E) + P(F)
  If the event is not mutually exclusive, then
• P(E ∪ F) = P(E) + P(F) – P(E and F together)
  Note: P (neither E nor F) = 1 – P(E or F).

9. Complement of an event

• For any event A, there exists another event A‘ which shows the remaining elements of the sample space S. A’ denotes the complementary event of A.

  A’ = S – A.
  Event A and A’ are mutually exclusive and exhaustive.
  Consider the example of tossing a coin. Let P(E) denote the probability of getting a tail when a coin is tossed. Then,
  

10. Multiplication Rule

When two events, A and B, are independent, the probability of both occurring is:
P(A and B) = P(A ∩ B) = P(A) × P(B)

11. Binomial Distribution

• In binomial probability distribution, the number of ‘Success’ in a sequence of n experiments, where each time a question is asked for yes-no, then the boolean-valued outcome is represented either with success/yes/true/one (probability p) or failure/no/false/zero (probability q = 1 − p).
•  A single success/failure test is also called a Bernoulli trial or Bernoulli experiment, and a series of outcomes is called a Bernoulli process. 
• For n = 1, i.e. a single experiment, the binomial distribution is a Bernoulli distribution. The binomial distribution is the base for the famous binomial test of statistical importance. 

• Example. A dice is tossed 5 times. What is the probability that 5 shows up exactly thrice?
  Sol. Here the 'random experiment' consists of tossing a die 5 times and observing the number '5' as success, then p = Probability of getting '5' with single dice = 1/6 so that q = 1-1/6 = 5/6
  Since the value of p is constant for each dice and the trials are independent, using formula for Binomial probability law, the probability of r successes is given by :
  
  Required probability that shows up exactly thrice is given by:
  
  
  
  Question for Introduction: Probability

  Try yourself:An unbiased dice is thrown. What is the probability of getting
  (i) an even number;
  (ii) a multiple of 3;
  (iii) an even number or a multiple of 3;
  (iv) an even number & a multiple of 3?
  Choose the most appropriate option.

  • A.

    (1 / 3), (1 / 2), (2 / 3), (1 / 6)
  • B.

    (1 / 2), (1 / 3), (2 / 3), (1 / 6)
  • C.

    (1 / 2), (1 / 6), (2 / 3), (1 / 3)
  • D.

    (1 / 6), (1 / 3), (2 / 3), (1 / 2)

  Explanation

  In a single throw of an unbiased dice, you can get any one of the outcomes 1, 2, 3, 4, 5, 6. So, exhaustive number of cases = 6.
  (i) An even number is obtained if you obtain any one of 2, 4, 6 as an outcome.
  So, favourable number of cases = 3.
  Thus, required probability =  (3 / 6) = (1 / 2)
  (ii) A multiple of 3 is obtained if you obtain any one of 3, 6 as an outcome. So, favourable number of cases = 2.
  Thus, required probability =  (2 / 6) = (1 / 3)
  (iii) An even number or a multiple of 3 is obtained in any of the following outcomes 2, 3, 4, 6. So, favourable number of cases = 4.
  Thus, required probability = (4 / 6) = (2 / 3)
  (iv) An even number and a multiple of 3 is obtained if you get 6 as an outcome. So, favourable number of cases = 1.
  Thus, required probability =  (1 / 6)

  Report a problem

  Cancel Report

  View Solution
  
  Example. Harshad and Amit throw with two dice. If Harshad throws 10, what is Amit’s chance of throwing a higher number?
  Sol. Total number of outcomes of throwing two dice is 6 × 6 = 36.
  Amit must throw either 11 or 12.
  This can be done in 3 ways namely (6 + 5, 5 + 6, 6 + 6)
  Thus Amit’s chance of throwing a higher number is 3/36 or 1/12.