Introduction: Ratio, Proportion & Variation | General Aptitude for GATE - Mechanical Engineering PDF Download
Understanding ratios, proportions, and variations is crucial for aptitude exams as these topics frequently show up particularly in questions involving changes and comparisons in ratios. Questions from this topic are based on conceptual clarity and their different applications.
Ratio
- When comparing any two numbers, sometimes, it is necessary to find out how many times one number is greater (or less) than the other. In other words, we often need to express one number as a fraction of the other.
- The numerator of the ratio is called the antecedent and the denominator is called the consequent of the ratio.
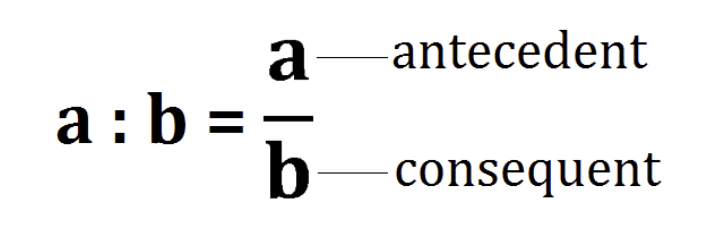
- The ratio of any number of quantities is expressed after removing any common factors that ALL the terms of the ratio have. For example, if there are two quantities having values of 4 and 2, their ratio is 4: 2, i.e., 2: 1 after taking the common factor 1 between them out.
- Ratios can be expressed as percentages. To express the value of a ratio as a percentage, we multiply the ratio by 100. Thus, 4/5 = 0.8 = 80%
Properties of Ratios
- If two quantities whose values are A and B respectively are in the ratio a : b, since we know that some common factor k(>0) would have been removed from A and B to get the ratio a: b, we can write the original values of the two quantities (i.e., A and B) as ak and bk respectively.
Example: If the salaries of two persons are in the ratio 7: 5, we can write their individual salaries as 7k and 5k respectively. - A ratio a: b can also be expressed as a/b. So if two items are in the ratio 2 : 3, we can say that their ratio is 2/3. If two terms are in the ratio 2, it means that they are in the ratio of 2/1, i.e., 2: 1.
- A ratio is said to be a ratio of greater or less inequality or of equality according to as antecedent is greater than, less than or equal to consequent.
In other words:
(i) The ratio a: b where a > b is called a ratio of greater inequality (example 3: 2)
(ii) The ratio a: b where a < b is called a ratio of less inequality (example 3: 5)
(iii) The ratio a: b where a = b is called a ratio of equality (example 1: 1)
From this, we can find that a ratio of greater inequality is diminished and a ratio of less inequality is increased by adding the same quantity to both terms, i.e., in the ratio a : b.
- When we add the same quantity x (positive) to both the terms of the ratio, we have the following results:
(i) if a < b then (a + x) : (b + x) > a : b
(ii) if a > b then (a + x) : (b + x) < a : b
(iii) if a = b then (a + x) : (b + x) = a : b
Types of Problems in Ratios
➢ Type - 1: As a bridge between 3 or more quantities
- Suppose you have a ratio relationship given between the salaries of two individuals A and B. Further, if there is another ratio relationship between B and C. Then, by combining the two ratios, you can come up with a single consolidated ratio between A, B and C. This ratio will give you the relationship between A and C.
Example 1: The Ratio of A’s salary to B’s salary is 2:3. The ratio of B’s salary to C’s salary is 4:5. What is the ratio of A’s salary to C’s salary?
Using the conventional process in this case:
- Take the LCM of 3 and 4 (the two values representing B’s amount). The LCM is 12.
- Convert B’s value in each ratio to 12.
- Thus, Ratio 1 = 8/12 and Ratio 2 = 12/15
- Thus, A:B:C = 8:12:15 Hence, A:C = 8:15
- Further, if it were given that A's salary was 800, you could derive the values of C's salary (as 1500).
Shortcut for this Process:
- The LCM process gets very cumbersome, especially if you are trying to create a bridge between more than 3 quantities.
- Suppose, you have the ratio train as follows: A:B = 2:3 B:C = 4:5 C:D = 6:11 D:E = 12:17
- In order to create one consolidated ratio for this situation, using the LCM process becomes too long.
- The shortcut goes as follows:
A : B : C : D : E can be written directly as:
2 * 4 * 6 * 12 : 3 * 4 * 6 * 12 : 3 * 5 * 6 * 12 : 3 * 5 * 11 * 12 : 3 * 5 * 11 * 17
➢ Type- 2: Ratio as a Multiplier
- The moment we say that the ratio of two numbers A and B is 5: 1, what we mean to say that A is 5 times B.
- It can also be seen that A: B: C in A/2: B/3: C/4 = K is not the same as A: B: C = 1/2: 1/3: 1/4 since the multiplier of A, B and C are not the same in both the cases.
- Ratio of A : B : C in A/2 : B/3 : C/4 = K can be calculated in the following way Since A/2 = B/3 = C/4 = K,
so, A= 2K, B = 3K and C = 4 K
Hence, the ratio of A:B:C = 2:3:4.
While calculating the ratio of A, B and C in A: B: C = 1/2: 1/3: 1/4, we will multiply each of A, B and C by the LCM of the denominator of all the ratios, i.e., 12.
So, A : B : C = 6 : 4 : 3
Example 2: 10 persons can cut 8 trees in 12 days. How many days will 8 persons take to cut 6 trees?
- Let us see this question from a changed perspective.
- Suppose if the question is: 10 persons can cut 8 trees in 12 days. How many days will 10 persons take to cut 4 trees?
- The answer to this question is: Since the amount of work is getting halved, so the number of days will also get halved.
There are three factors, namely:
(i) The number of men
(ii) The number of days
(iii) The number of trees
which are responsible for the final answer.- Since the number of men is less in the final situation, so more days will be required.
- Hence, multiplier = 10/8 (had there been 12 persons, the multiplier would have been 10/12.)
- The number of trees is less in the final situation, so fewer number of days will be required. So, multiplier = 6/8
- Hence, the total number of days = 12 x 10/8 x 6/8 = 90/8 = 11.25 days
Example 3: Two numbers are in the ratio 3: 4. What part of the larger number must be added to each number so that their ratio becomes 5: 6?
- Let the two numbers be 3x and 4x.
- 3x + k/4x + k = 5/6
- 18x + 6k = 20x + 5k
- k = 2x
- ∴ Half of the larger number must be added to each number.
Example 4: There are 2 classes A and B. If 10 students leave class A and join class B, then the ratio of the number of students in class A and class B would reverse. Find the difference in the numbers of students in class A and class B.
- Let the numbers of students in class A and class B be ax and bx, respectively.
- Given:
⇒ ax - 10/bx + 10 = b/a
⇒ a2x − 10a = b2x + 10b
⇒ a2x – b2x – 10a – 10b = 0
⇒ (ax – bx – 10) (a + b) = 0- ∴ ax – bx = 10
- The difference in the number of students in class A and class B is 10.
Proportion
When two ratios are equal, the four quantities composing them are said to be proportional.
Thus if a/b = c/d, then a,b, c, d are proportionals. This is expressed by saying that a is to b as c is to d, and the proportion is written as
a:b :: c :d
or
a: b = c : d
- The terms a and d are called the extremes while the terms b and c are called the means.

• If four quantities are in proportion, the product of the extremes is equal to the product of the means.
Let a, b, c, d be the proportional.
Then by definition a/b = c/d
Therefore, ad = bc
Hence if any three terms of proportion are given, the fourth may be found.
Thus if a, c, d are given, then b = ad/c.
• If three quantities a, b and c are in continued proportion, then
a : b = b : c
Therefore, ac = b2
In this case, b is said to be a mean proportional between a and c; and c is said to be a third proportional to a and b.
• If three quantities are proportional the first is to the third is the duplicate ratio of the first to the second.
That is: for a:b :: b: c
a: c = a2 :b2
• If four quantities a, b, c and d form a proportion, many other proportions may be deduced by the properties of fractions. The results of these operations are very useful. These operations are:
Invertendo: If a/b = c/d then b/a = d/c
Alternando: If a/b = c/d, then a/c = b/d
Componendo: If a/b=c/d, then (a+b)/b=(c+d)/d
Dividendo: If a/b=c/d, then (a-b)/b=(c-d)/d
Tips and Tricks on Proportion
1. a/b = c/d ⇒ ad = bc
2. a/b = c/d ⇒ b/a = d/c
3. a/b = c/d ⇒ a/c = b/d
4. a/b = c/d ⇒ (a + b)/b = (c + d)/d
5. a/b = c/d ⇒ (a - b/b = (c - d)/d
6. a/(b + c) = b/(c + a) = c/(a + b) and a + b + c ≠0, then a = b = c.
7. a/b = c/d ⇒ (a + b)/(a - b) = (c + d)/(c - d), which is known as componendo -dividendo rule
8. If both the numbers a and b are multiplied or divided by the same number in the ratio a:b, then the resulting ratio remains the same as the original ratio.
Types of Proportions
Based on the type of relationship two or more quantities share, the proportion can be classified into different types. There are two types of proportions.
(i) Direct Proportion
(ii) Inverse Proportion
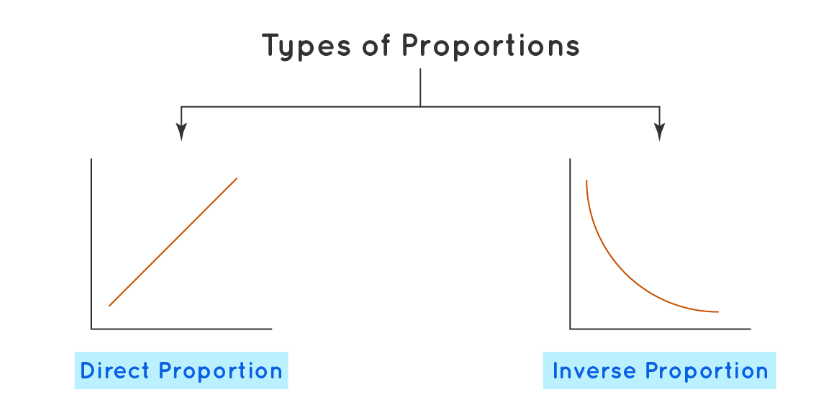
Direct Proportion
- This type describes the direct relationship between two quantities.
- In simple words, if one quantity increases, the other quantity also increases and vice-versa.
- For example, if the speed of a car is increased, it covers more distance in a fixed amount of time. In notation, the direct proportion is written as y ∝ x.
Inverse Proportion
- This type describes the indirect relationship between two quantities.
- In simple words, if one quantity increases, the other quantity decreases and vice-versa. In notation, an inverse proportion is written as y ∝ 1/x.
- For example, increasing the speed of the car will result in covering a fixed distance in less time.
Types of Problems in Proportion
Example 1:
Given that both x and y vary directly from each other. If x = 10 and y = 15, which of the following pairs is not possible with respect to the value of x and y?
x = 2 and y = 3
x = 8 and y = 12
x = 15 and y = 20
x = 25 and y = 37.5
Solution:
Given that x and y are directly proportional.
Hence, x/y = k(constant)
So, x/y = 10/15 = 2/3 …(1)
Now, check with the options provided here.
(a) x = 2 and y = 3
x/y = 2/3 …(2)
Hence, (1) = (2)
(b) x = 8 and y = 12
x/y = 8/12 = 2/3 …(3)
Hence, (1) = (3)
(c) x = 15 and y = 20
x/y = 15/20 = 3/4 …(4)
Hence, (1) ≠ (4)
(d) x = 25 and y = 37.5
x/y = 25/37.5 = 2/3 …(5)
Hence, (1) = (5)
Therefore, option (c) x = 15 and y = 20 should not be a possible pair with respect to the values x and y.
Example 2:
Ramya purchased 97 meters of cloth that cost Rs. 242.50. What will the length of the cloth be if she purchased it for Rs. 302.50.
Solution:
As we know, the length of the cloth and its costs are directly proportional. Because if we purchase more, the cost will be higher. Similarly, if we purchase less, the cost will decrease.
Hence, we get
| Length (in Meters) | 97 | x |
| Cost (in Rs) | 242.50 | 302.50 |
Now, we have to find the value of “x”.
Since the length and cost of cloth are directly proportional, we can write
97/242.50 = x/302.50
Now, cross multiply the above equation, we get
242.50x = 97(302.50)
242.50x = 29342.5
Hence, x = 29342.5 / 242.50 = 121.
Hence, the length of the cloth is 121 meters, if she purchased it for Rs. 302.50.
Therefore,
| Length (in Meters) | 97 | 121 |
| Cost (in Rs) | 242.50 | 302.50 |
Variation
Two quantities A and B are said to vary with each other if there is some relationship between A and B such that the change in A and B is uniform and guided by some rule.➢ Some Typical Examples of Variation
- Area (A) of a circle = π.R2, where R is the radius of the circle. Area of a circle depends upon the value of the radius of a circle, or, in other words, we can say that the area of a circle varies as the square of the radius of a circle.
- At a constant temperature, the pressure is inversely proportional to the volume.
- If the speed of any vehicle is constant, then the distance traversed is proportional to the time taken to cover the distance.
Types of Variation

1. Direct Variation
When it is said that A varies directly as B, you should understand the following implications:
(a) Logical Implication: When A increases B increases.
(b) Calculation Implication: If A increases by 10%, B will also increase by 10.
(c) Graphical Implications: The following graph is representative of this situation.
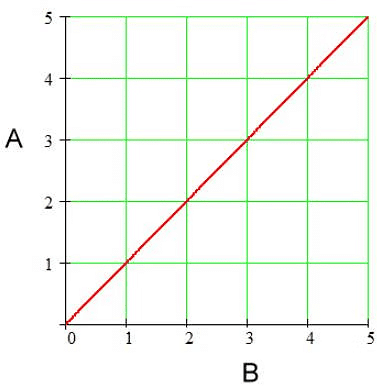
2. Inverse Variation
When A varies inversely as B, the following implication arises.(a) Logical Implication: When A increases B decreases.
(b) Calculation Implication: If A decreases by 9.09%, B will increase by 10%.
(c) Graphical Implications: The following graph is representative of this situation.
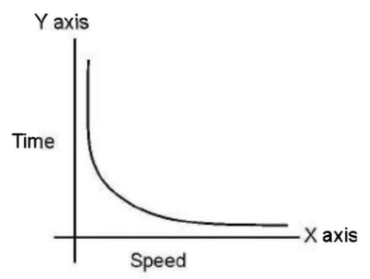
(d) Equation Implication: The product A X B is constant.
Example : The height of a tree varies as the square root of its age (between 5 and 17 years). When the age of a tree is 9 years, its height is 4 feet. What will be the height of the tree at the age of 16?
Sol: Let us assume the height of the tree is H and its age is A years.
So, H ∝ √A, or, H = K x √A Now, 4 = K x √9 K = 4/3
Height at the age of 16 years = H = K x √A
= 4/3 x 4
= 16/3 = 5 feet 4 inches.
Note: For problems based on this chapter we are always confronted with ratios and proportions between different number of variables. For the above problem we had three variables which were in the ratio of 4 : 6 : 9. When we have such a situation we normally assume the values in the same proportion, using one unknown ‘x’ only (in this example we could take the three values as 4x, 6x and 9x, respectively).Then, the total value is represented by the addition of the three giving rise to a linear equation, which on a solution, will result in the answer to the value of the unknown ‘x’.
Solved Examples
Q1: A student gets an aggregate of 60% marks in five subject in the ratio 10 : 9 : 8 : 7 : 6. If the passing marks are 50% of the maximum marks and each subject has the same maximum marks, in how many subjects did he pass the examination?
(a) 2
(b) 3
(c) 4
(d) 5
Answer: Option (c)
Solution:
Let his marks be 10, 9, 8, 7 and 6 in the five subjects. Hence, totally he has scored 40 marks. This constitutes only 60% of the total marks. Hence, total marks 40/0.6 = 66.7 or 67 approx. , which is the maximum marks in all 5 subjects.
Since the total marks in each subject is the same, hence maximum marks in each subject will be 67/5 = 13 approx. Out of this 50% is the passing marks . In other words to pass in a subject, he needs to score 6.5 marks. We can see that only in 1 subject, he scored less than this viz. 6. Hence, he passed in 4 subject.
Q2: Total salary of A, B & C is Rs.350. If they spend 75%, 80% & 56% of their salaries respectively their savings are as 10 : 12 : 33. Find the salary of C?
(a) 80
(b) 150
(c) 180
(d) None of These
Answer: Option (b)
Solution:
A’s saving = 100 – 75 = 25% of his salary. B’s saving = 100 – 80 = 20% of his salary C’s saving = 100 – 56 = 44% of his salary 25/100 of A’s salary : 20/100 of B’s salary : 44/100 of C’s salary = 10 : 12 : 33
or 25 × A’s salary : 20 × B’s salary : 44 × C’s salary = 10 : 12 : 33
or 25 × A’s salary / 20 × B’s salary = 10/12
or A’s salary : B’s salary = 2 : 3,
B’s salary : C’s salary = 4 : 5
Thus A : B = 2 : 3, B : C = 4 : 5 Now making B common we have
A : B = 8 : 12, B : C = 12 : 15, or A : B : C = 8 : 12 : 15
Total salary = 350 Þ A’s salary = 8 / (8 + 12 + 15) × 350 = 80
B’s salary = 12 / (8 + 12 + 15) = 120, and C’s Salary = 150
Q3: Arvind Singh purchased a 40 seater bus. He started his services on route number 2 (from Mahu Naka to Dewas Naka with route length of 50 km). His profit (P) from the bus depends upon the number of passengers over a certain minimum number of passengers ‘n’ and upon the distance travelled by bus. His profit is Rs.3600 with 29 passengers in the bus for a journey of 36 km and Rs.6300 with 36 passengers in the bus for a journey of 42 km. What is the minimum number of passengers are required so that he will not suffer any loss.
(a) 12
(b) 20
(c) 18
(d) 15
Answer: Option (d)
Solution:
The minimum number of passengers n, at which there is no loss and number of passengers travelling = m
and let the distance travelled is d, Then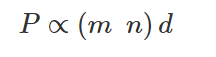
or p = k(m – n)d? k is a constant.
When P = 3600, m = 29 and d = 36, then
3600 = k(29 – n) × 36 ...(1)
Again, when p = 6300, m = 36, d = 42, then
6300 = k(36 – n) × 42 ...(2)
Dividing equation (2) by (1)
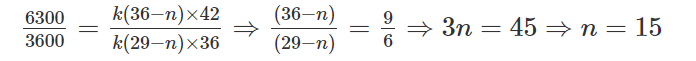
|
193 videos|169 docs|152 tests
|
FAQs on Introduction: Ratio, Proportion & Variation - General Aptitude for GATE - Mechanical Engineering
| 1. What is the definition of a ratio and how is it represented? |  |
| 2. What are the key properties of ratios? |  |
| 3. What types of problems are commonly encountered in ratios? |  |
| 4. What is the difference between proportion and ratio? |  |
| 5. What are the different types of variation and how do they relate to ratios and proportions? |  |

















