Introduction: Real Numbers | Advance Learner Course: Mathematics (Maths) Class 9 PDF Download
Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also.
At the same time, the imaginary numbers are the un-real numbers, which cannot be expressed in the number line and is commonly used to represent a complex number. The concepts related to real numerals are explained here in detail, along with examples and practice questions. The key concept in the number system is included in this article.
Example: 23, -12, 6.99, 5/2, π(3.14)
Real Numbers Definition
Real numbers can be defined as the union of both the rational and irrational numbers. They can be both positive or negative and are denoted by the symbol “R”. All the natural numbers, decimals and fractions come under this category. See the figure, given below, which shows the classification of real numerals.
Set of Real Numbers
The set of real numbers consist of different categories, such as natural and whole numbers, integers, rational and irrational numbers. In the table given below, all these numbers are defined with examples.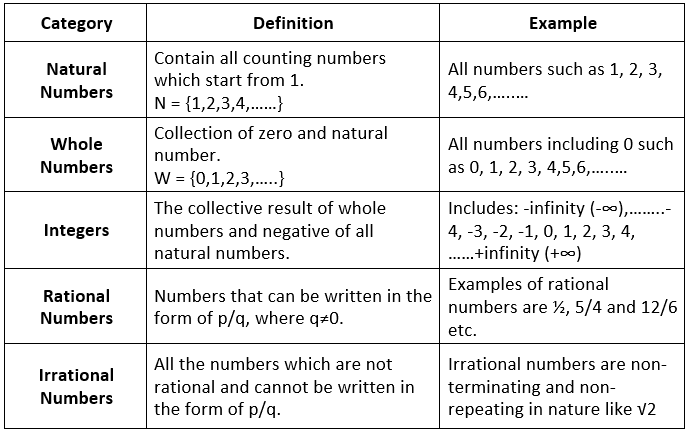
Real Numbers Chart
The chart for the set of real numerals including all the types are given below: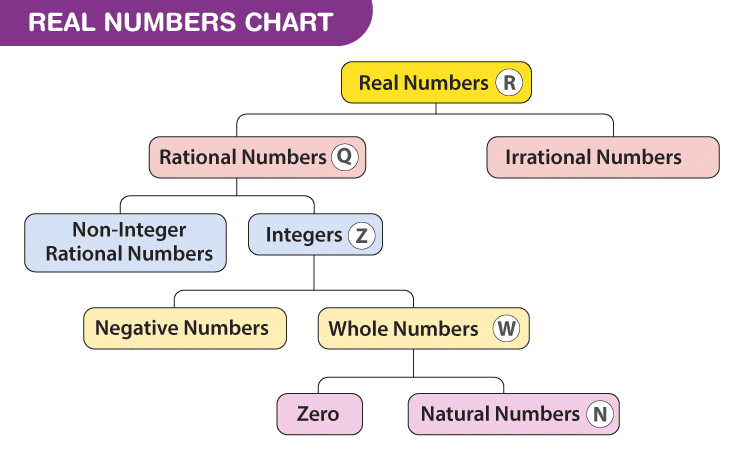
Properties of Real Numbers
There are four main properties which include commutative property, associative property, distributive property and identity property. Consider “m, n and r” are three real numbers. Then the above properties can be described using m, n, and r as shown below:
1. Closure Property
The sum and product of two real numbers is always a real number.
The closure property of R is stated as follows: For all a, b ∈ R, a + b ∈ R and ab ∈ R
2. Commutative Property
If m and n are the numbers, then the general form will be m + n = n + m for addition and m.n = n.m for multiplication.
- Addition: m + n = n + m.
Example: 5 + 3 = 3 + 5, 2 + 4 = 4 + 2 - Multiplication: m × n = n × m.
Example: 5 × 3 = 3 × 5, 2 × 4 = 4 × 2
3. Associative Property
If m, n and r are the numbers. The general form will be m + (n + r) = (m + n) + r for addition(mn) r = m (nr) for multiplication.
- Addition: The general form will be m + (n + r) = (m + n) + r. An example of additive associative property is 10 + (3 + 2) = (10 + 3) + 2.
- Multiplication: (mn) r = m (nr). An example of a multiplicative associative property is (2 × 3) 4 = 2 (3 × 4).
4. Distributive Property
For three numbers m, n, and r, which are real in nature, the distributive property is represented as:
m (n + r) = mn + mr and (m + n) r = mr + nr.
Example: 5(2 + 3) = 5 × 2 + 5 × 3. Here, both sides will yield 25.
5. Identity Property
There are additive and multiplicative identities.
- For addition: m + 0 = m. (0 is the additive identity)
- For multiplication: m × 1 = 1 × m = m. (1 is the multiplicative identity)
|
13 videos|79 docs|29 tests
|
FAQs on Introduction: Real Numbers - Advance Learner Course: Mathematics (Maths) Class 9
| 1. What are real numbers? |  |
| 2. What are the properties of real numbers? |  |
| 3. How are real numbers different from rational numbers? |  |
| 4. Can real numbers be negative? |  |
| 5. How are real numbers used in everyday life? |  |
|
13 videos|79 docs|29 tests
|

|
Explore Courses for Class 9 exam
|

|


















