Introduction to Heat Transfer | General Awareness - Bank Exams PDF Download
Introduction
- Heat transfer is a subject of widespread interest to the students of engineering curriculum, practicing engineering and technicians engaged in the design, construction, testing and operation of the many diverse forms of heat exchange equipment required in our scientific and industrial technology. While launching ourselves into the frontiers of heat transfer, let us recall the following basic concepts and definitions.
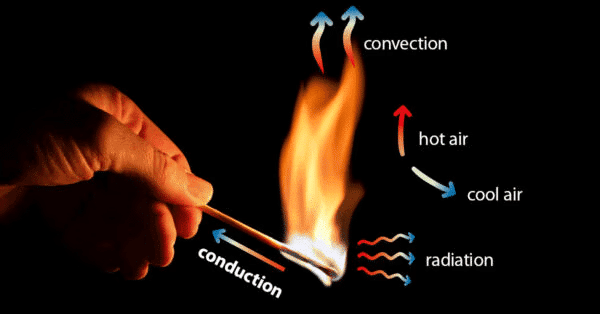
- In thermodynamics that when two systems are brought into contact through some kind of wall, energy transfers such as heat and work take place between them, Work is a transfer of energy to a particle which is evinced by changes in its position when acted upon by a force. Heat like work, is energy in the process of being transferred.
- The transfer and conversion of energy from one form to another is basic to all heat transfer process, and hence they are governed by the first as well as the second law of thermodynamics. The major difference between thermodynamics and heat transfer is that the former deals with the relation between heat and other forms of energy, whereas the latter is concerned with the analysis of rate of heat transfer. Heat transfer is commonly associated with fluid dynamics by providing supplements the law of thermodynamics by providing additional experimental rules to establish energy transfer rates.
Modes of Heat Transfer
The energy transfer as heat takes place by three distinct modes: conduction, convection and radiation.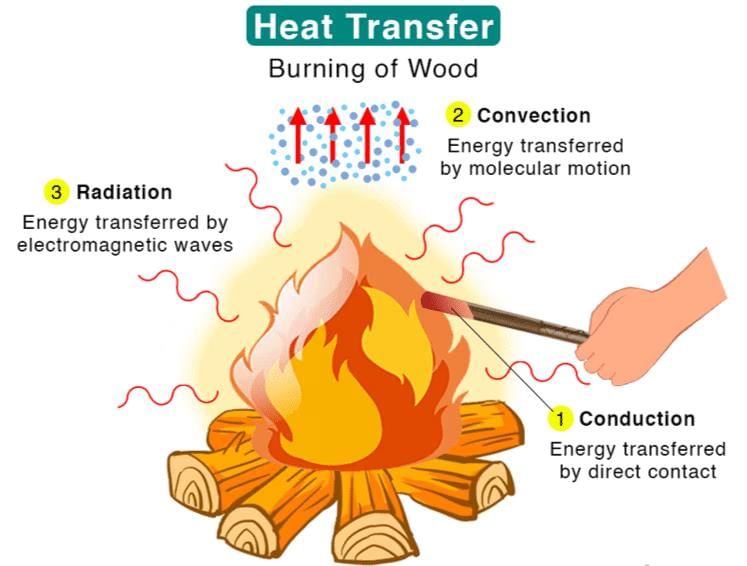
- Conductions: Thermal conduction is a mechanism of heat propagation from a region of higher temperature to a region of low temperature within a medium (solid, liquid or gaseous) or between two mediums which are in direct physical contact with each other. Example: the heating of the metal rod from one end by heat source. In this case, the heat is transferred from one end to other end by conduction.
- Convections: Thermal convection is a process of energy transport affected by the circulation medium (gas, liquid or a powder substance). Convection is possible only in a fluid medium and is directly linked with the transport of medium itself.
In natural convection, the circulation of the fluid medium is caused by buoyancy effects, i.e. by the difference in densities of the cold and heated particles.
In forced convection, the flow of fluid is caused by a pump, fan or by atmospheric winds. These mechanical devices provides a definite circuit for the circulating currents and that speeds up the heat transfer rate. - Radiation: Thermal radiation is the transmission of heat in the form of radiant energy or wave motion from one body to another across an intervening space.
One Dimensional Heat Conduction
Consider one dimensional heat conduction through a homogeneous, isotropic wall of thickness d with contact thermal conductivity k and constant cross sectional area A. The wall is insulated on its lateral faces and constant but different temperatures t1 and t2 are maintained at its boundary surfaces. Obviously temperature varies only in the direction normal to the wall and temperature potential causes heat transfer in the positive x direction. Starting with general heat equation in Cartesian coordinates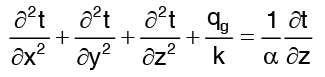 …(1)
…(1)
with stipulations of 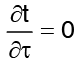 (steady state)
(steady state)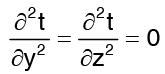 (for one dimensional)
(for one dimensional)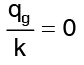 (where there is no internal generation of heat)
(where there is no internal generation of heat)
The conduction equation transforms to 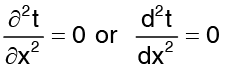 …(2)
…(2)
This second order differential equation can be twice integrated with respect to x to give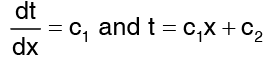 …(3)
…(3)
The constant of integration are evaluated with regard to the boundary conditions relevant to the flow situation. Here the boundary conditions are the known temperatures. That is t = t1 at x = 0 and t = t2 at x = δ. When these boundary conditions are applied to the equation (3) for temperature distributions, t1 = 0 + c2 and t2 = c1 δ + c2 Accordingly the expression for temperature profile becomes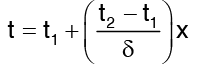 …(4)
…(4)
The temperature distribution is thus linear across the wall.
Equation (4) does not involve thermal conductivity, a conclusion may be drawn that temperature distribution of the material, whether it is steel, wood or asbestos. Computation for heat flow rate can be made by substituting equation.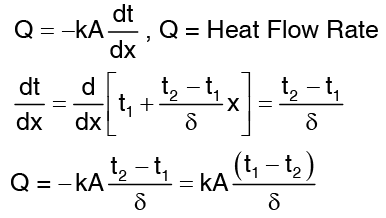 …(5)
…(5)
Obviously the heat flow rate is a constant in independent of x.
Conduction through a Composite Wall
A composite wall refers to a wall of a several heterogeneous layers e.g. wall of dwelling houses where bricks are given a layer of plaster on either side.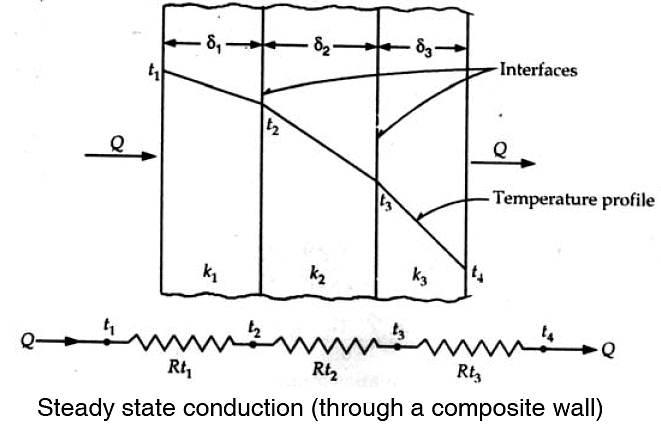
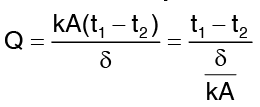
Comparing the above expression for Q with the current equation in electricity 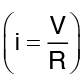 we get,
we get,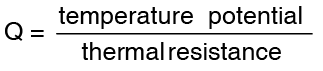
Hence,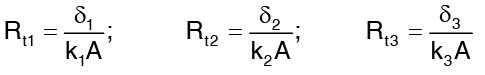
The figure below shows one such composites wall having three layers of different materials δ1, δ2, δ3 and their thermal conductivities correspond to the average temperature conduction. The surface temperature of the wall are t1 and t4 and the temperatures at the interfaces are t2 and t3. Under steady state condition, heat flow does not vary across wall i.e. is same for every layer. Thus,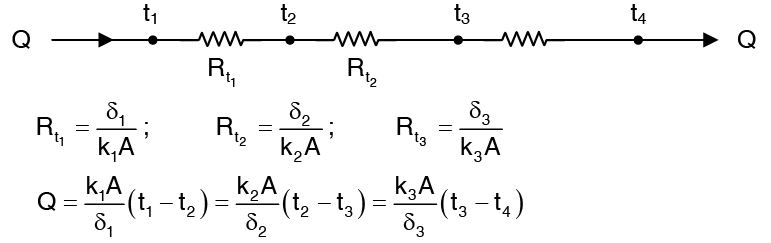
Rewriting the above expression in terms of temperature drop across each layer, 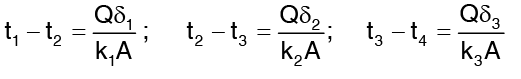
Summation gives the overall temperature difference across the wall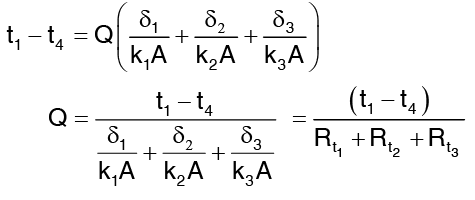
Distributing of temperature in a plane multilayer wall is represented by a polygonal line (Fig. in previous page) when the above analysis is extended to a n layer composite wall one obtains :
where 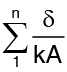 is sum of the thermal resistances of difference layers comprising the composite wall.
is sum of the thermal resistances of difference layers comprising the composite wall.
Radial Heat Conduction Through Cylindrical Systems
Consider a long cylinder of inside radius ri outside radius ro and length L 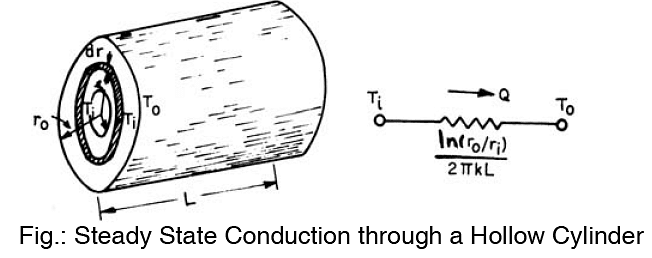
We consider the cylinder to be long so that the end losses are negligible. The insider and outside surfaces are kept at constant temperature ti and to respectively. A steam pipe in a room can be taken as an example of a long hollow cylinder.
The general heat conduction equation in cylinder coordinates is :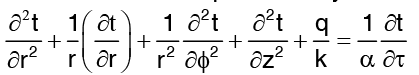 …(1)
…(1)
Assuming that heat flows only in a radial direction, the above equation under steady states (without beat generation) takes the form.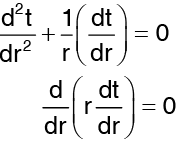 …(2)
…(2)
Subject to the boundary conditions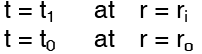
Integrating Equation (2) twice we get
using the boundary conditions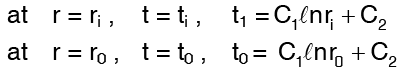
The solutions for above equations for Q is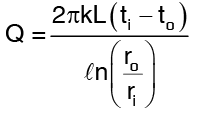 …(3)
…(3)
So Rt, the thermal resistance now becomes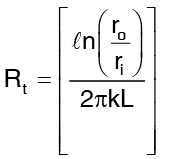 …(4)
…(4)
Log Mean Area
Let us now consider a cylinder and a slab, both made of the same material, let Ti and To be the temperature maintained on the two sides of the plane slab and also on the inside and outside of the cylinder respectively. Let ri and ro be inside and outside radii of the cylinder and let the thickness of the slab be equal to (ro - ri)
Heat flow through cylinder, by equation (3) = 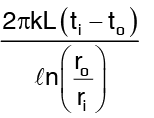
Heat flow through slab, by equation = 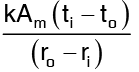
where Am is taken is such a way that the heat flows through the cylinder and the slab are equal for the same temperature difference across them. 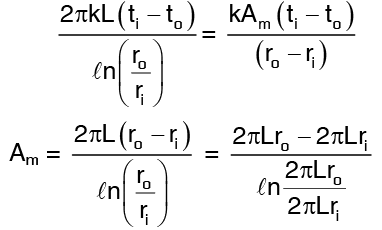
or 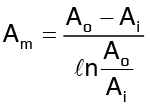
where Ai and Ao are the inside and outside surface areas of the cylinder.
Am is called the log mean area of the cylinder, and can be used to transform a cylinder into an equivalent slab. It so turns that if 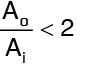
then Am can be taken as an average area = 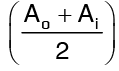
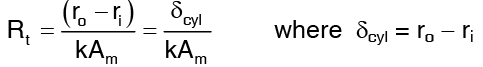
The thermal resistance of a hollow cylinder is of exactly the same form as that for slab except that the logarithm mean area is used of cylinder.
Radial Heat Conduction Through Spherical Systems
Consider a hollow sphere whose inside and outside surfaces are held at constant temperature ti and to respectively.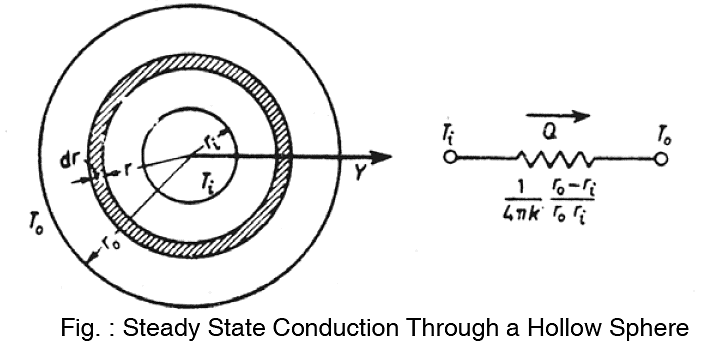
If the temperature variation is only in radial direction, then for steady state conditions with no heat generation, the heat conduction equation simplifies to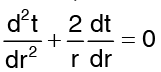
Multiplying throughout by r2, we get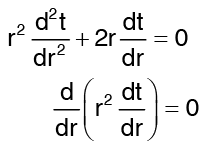 …(1)
…(1)
Integration of equation (1) gives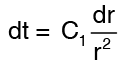
Integrating again, we get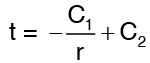
Applying the boundary conditions,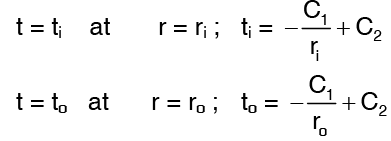
Solving the above equations we get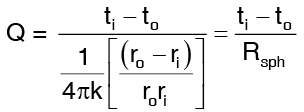
where the thermal resistance of a sphere is defined as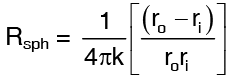 …(2)
…(2)
Geometric Mean Area
Rsph can be rearranged as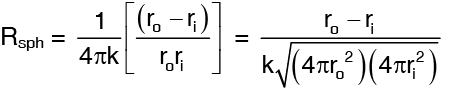
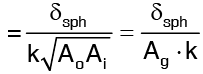 …(3)
…(3)
where Ai and Ao are the areas of the inner and outer surfaces of the sphere
δsph = ro - ri = thickness of sphere. 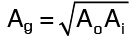 …(4)
…(4)
is called the geometric mean area of the sphere. The thermal resistance of a sphere given by equation (4) is similar to that of a plane wall except that the area is replaced by the geometric mean area.
Solved Numericals
Example 1: A hollow cylinder 5cm. Inner diameter and 10 cm outer diameter has an inner surface temperature of 200°C and an outer surface temperature of 100°C. Determine the temperature of the point halfway between the inner and the outer surfaces. If the thermal conductivity of the cylinder material is 70 W/mk. Determine the heat flow through the cylinder per linear metre.
Solution: Equation (3) gives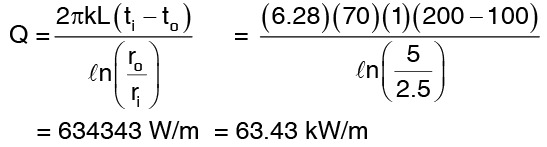
At half way between ri and ro radius 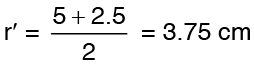
Since Q remains the same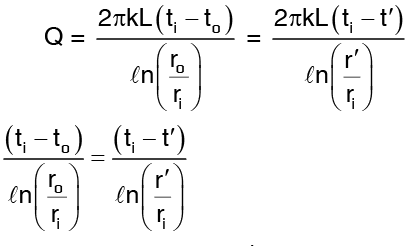
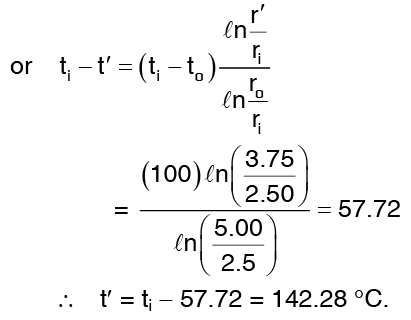
Example 2: Calculate the rate of heat loss for a red brick wall of length 5m, height 4m and thickness 0.25m. The temperature of the inner surface is 110°C and that of the outer surface is 40°C. The thermal conductivity of red brick, k = 0.70 W/mk. Calculate also the temperature at an interior point of the wall 20 cm distant from the inner wall.
Solution: Considering a plane homogenous wall the thickness of which is considerably less than its width and height, the one dimensional heat conduction equation (5) can be applied.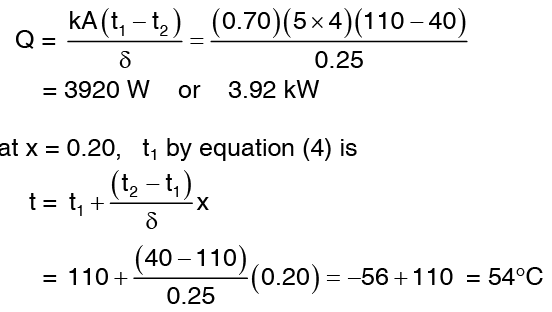
Example 3: A rod of 3 cm diameter and 20 cm length is maintained at 100°C at one end and 10°C at the other end. These temperature conditions are attained when there is heat flow rate of 6 watts. If cylindrical surface of the rod is completely insulated, determined the thermal conductivity of the rod material.
Solution: Involving Fourier law of heat conduction, the heat flow rate through the rod is given by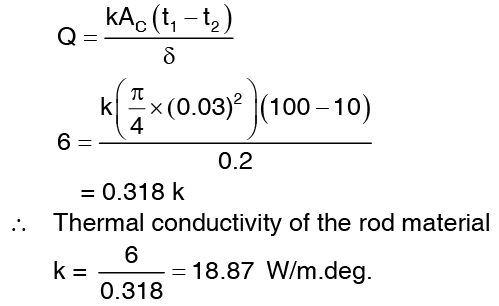
Example 4: A hollow sphere 10 cm inner diameter and 30 cm outer diameter of a material having thermal conductivity 50 W/mk is used as a container for a liquid chemical mixture. Its inner and outer surface temperatures are 300°C and 100°C respectively. Determine the heat flow rate through the sphere. Also estimate the temperature at a point a quarter of the way between the inner and outer surfaces.
Solution: Referring to equation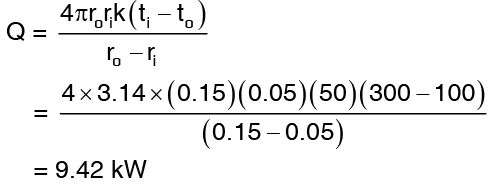
The value of r at one fourth way of the inner and outer surface is 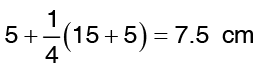 temperature at r = 7.5 cm is
temperature at r = 7.5 cm is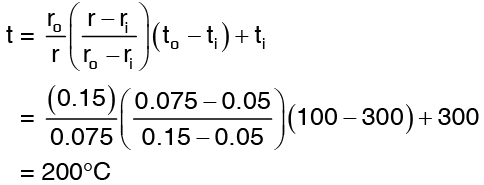
Voltage required for a given temperature rise in a wire heated by an electric current: It can be shown that the voltage required is 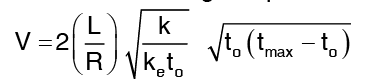 where
where
L = length of wire (conductor)
R = radius of wire (conductor)
k = Thermal conductivity; ke = electrical conductivity.
to = temperature of outer surface of wire
tmax = temperature at the centre of wire along axis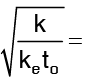 Lorentz number which shows the relation between. Thermal conductivity and electrical conductivity.
Lorentz number which shows the relation between. Thermal conductivity and electrical conductivity.
Example 5: A storage chamber of interior dimension 10m x 8m x 2.5m high has its inside maintained at a temperature of -20°C while the outside is at 25°C. The wall and ceiling of the chamber have three layer made of
60 mm thick board (k = 0.2 W/m deg) on the inside
90 mm thick insulation (k = 0.04 W/m deg) at mid
240 mm thick concrete (k = 1.8 W/m deg) on the outside
Neglecting flow of heat through the floor, determine the rate at which heat can flow towards inside of the chamber.
Solution: Neglecting corners and edges, the area of heat flow is A = 2 (1 0 ´2.5)+ 2 ( 8 ´2.5 )+ (10 ´8 ) = 170m2Recalling that thermal resistance for a slab of thickness d, conductivity k and area A equal d/kA, we get
|
365 videos|700 docs|149 tests
|
FAQs on Introduction to Heat Transfer - General Awareness - Bank Exams
| 1. What are the different modes of heat transfer? |  |
| 2. How does one-dimensional heat conduction work? |  |
| 3. What is conduction through a composite wall? |  |
| 4. How does radial heat conduction through cylindrical systems work? |  |
| 5. What is the importance of log mean area and geometric mean area in heat transfer? |  |






















