Introduction to Limits | Mathematics (Maths) Class 11 - Commerce PDF Download
A. Definition of Limit
Let f be a function defined on an open interval containing c (except possibly at c) and let L be a real number. The statement 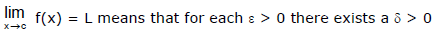 such that if
such that if 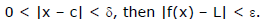
B. The Existence of a Limit
Let f be a function and let c and L be real numbers. The limit of f(x) as x approaches c is L if and only if
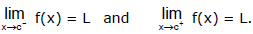
In other words limit of a function f(x) is said to exist as, x→a when
 =
=  = A finite quantity .
= A finite quantity .
Ex.1 The graph of a function g is shown in the figure. Use it to state the values (if they exist) of the following
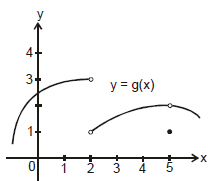
(a) 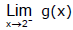
(b) 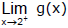
(c) 
(d) 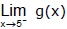
(e) 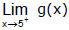
(f) 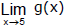
Sol. From the graph we see that the values of g(x) approach 3 as x approaches 2 from the left, but they approach 1 as x approaches 2 from the right. Therefore
 and
and 
(c) Since the left and right limits are different, we conclude that  g(x) does not exist.
g(x) does not exist.
The graph also show that
 and
and 
(f) This time the left and right limits are the same and so, we have 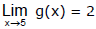
Despite this fact, notice that 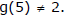
Ex.2 If f(x) = 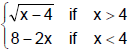 determine whether
determine whether 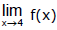 exists.
exists.
Sol.
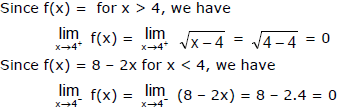

The right and left-hand limits are equal. Thus, the limit exists and 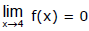 The graph of f is shown in the figure.
The graph of f is shown in the figure.
Ex.3 Evaluate  denotes the greatest integer function)
denotes the greatest integer function)
Sol.
Let P = 
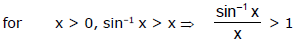
 R.H.L. =
R.H.L. = 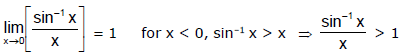
∴ L.H.L. = 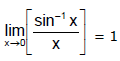
Hence P = 1.
C. FUNDAMENTAL THEOREMS ON LIMITS
Let b and c be real numbers, let n be a positive integer, and let f and g be functions with the following limits. 


 provided f is continuous at x = m.
provided f is continuous at x = m.

Ex.4 Evaluate the following limits and justify each step.


Sol. 


= 2(52) – 3(5) + 4 = 39
(b) We start by using laws of limit, but their use is fully justified only at the final stage when we see that the limits of the numerator and denominator exist and the limit of the denominator is not 0.



D. NON-EXISTENCE OF LIMIT
Three of the most common types of behaviour associated with the non-existence of a limit.
1. f(x) approaches a different number from the right side of c than it approaches from the left side.
2. f(x) increases or decreases without bound as x approaches c.
3. f(x) oscillates between two fixed values as x approaches c.
There are many other interesting functions that have unusual limit behaviour. An often cited one is the Dirichlet function f(x)  This function has no limit at any real number c.
This function has no limit at any real number c.
E. INDETERMINANT FORMS : 
Ex.5 Which of the following limits are in indeterminant forms. Also indicate the form




Sol. (i) No (ii) Yes 0/0 form (iii) Yes 0 × ∝ form (iv) Yes (∝ – ∝) form
(v) Yes, 00 form (vi) Yes ∝0 form (vii) Yes 1∝form (viii) No
Remark :
(i) ‘0’ doesn’t means exact zero but represent a value approaching towards zero similarly to ‘1’ and infinity.
(ii) ∝+ ∝= ∝(iii) ∝× ∝= ∝(iv) (a/∝) = 0 if a is finite
(v) a/0 is not defined for any a ε R.
(vi) a b = 0, if & only if a = 0 or b = 0 and a & b are finite.
|
75 videos|238 docs|91 tests
|
FAQs on Introduction to Limits - Mathematics (Maths) Class 11 - Commerce
| 1. What is a limit in calculus? |  |
| 2. How do you find the limit of a function? |  |
| 3. What is the importance of limits in calculus? |  |
| 4. Can a function have a limit at a point but not be defined at that point? |  |
| 5. Are all limits finite? |  |

|
Explore Courses for Commerce exam
|

|

















