Introduction to Prime Numbers | Quantitative for GMAT PDF Download
What is a Prime Number?
A prime number is a positive integer having exactly two factors. If p is a prime, then it’s only factors are necessarily 1 and p itself.
- Any number which does not follow this is termed as composite numbers which means that they can be factored into other whole numbers.
- First Ten Prime Numbers: The first ten primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Note: It should be noted that 1 is a non-prime number.
Prime Numbers 1 to 100 List
As we know, the prime numbers are the numbers that have only two factors which are 1 and the number itself. There are a number of primes in the number system. Here is the list provided of prime numbers that are present between 1 and 100, along with their factors and prime factorization.
| Prime Numbers between 1 and 100 | Factors | Prime Factorisation |
| 2 | 1, 2 | 1 x 2 |
| 3 | 1, 3 | 1 x 3 |
| 5 | 1,5 | 1 x 5 |
| 7 | 1,7 | 1 x 7 |
| 11 | 1,11 | 1 x 11 |
| 13 | 1, 13 | 1 x 13 |
| 17 | 1, 17 | 1 x 17 |
| 19 | 1, 19 | 1 x 19 |
| 23 | 1, 23 | 1 x 23 |
| 29 | 1, 29 | 1 x 29 |
| 31 | 1, 31 | 1 x 31 |
| 37 | 1, 37 | 1 x 37 |
| 41 | 1, 41 | 1 x 37 |
| 43 | 1, 43 | 1 x 43 |
| 47 | 1, 47 | 1 x 47 |
| 53 | 1, 53 | 1 x 53 |
| 59 | 1, 59 | 1 x 59 |
| 61 | 1, 61 | 1 x 61 |
| 67 | 1, 67 | 1 x 67 |
| 71 | 1, 71 | 1 x 71 |
| 73 | 1, 73 | 1 x 73 |
| 79 | 1, 79 | 1 x 79 |
| 83 | 1, 83 | 1 x 83 |
| 89 | 1, 89 | 1 x 89 |
| 97 | 1, 97 | 1 x 97 |
Why 1 is not a prime number?
Conferring to the definition of the prime number which states that a number should have exactly two factors for it to be considered as a prime number. But, number 1 has one and only one factor which is 1 itself. Thus, 1 is not considered as a Prime number.
Even Prime Number
As we know, the prime numbers are the numbers that have only two factors and the numbers that are evenly divisible by 2 are even numbers. Therefore, 2 is the only prime number that is even and the rest of the prime numbers are odd numbers, hence called odd prime numbers.
Twin Prime Numbers
The prime numbers that have only one composite number between them are called twin prime numbers or twin primes. The other definition of twin prime numbers is the pair of prime numbers that differ by 2 only. For example, 3 and 5 are twin primes because 5 – 3 = 2.
The other examples of twin prime numbers are:
- (5, 7) [7 – 5 = 2]
- (11, 13) [13 – 11 = 2]
- (17, 19) [19 – 17 = 2]
- (29, 31) [31 – 29 = 2]
- (41, 43) [43 – 41 = 2]
- (59, 61) [61 – 59 = 2]
- (71, 73) [73 – 71 = 2]
Coprime Numbers
The pair of numbers that have only one factor in common between them, are called coprime numbers. Prime factors and coprime numbers are not the same. For example, 6 and 13 are coprime because the common factor between them is 1 only.
Smallest Prime Number
The smallest prime number as defined by modern mathematicians is 2. To be prime, a number must be divisible only by 1 and the number itself which is fulfilled by the number 2.
Largest Prime Number
As of January 2016, the largest known prime number is 2{77,232,917} – 1, a number with 23,249,425 digits. It was found by the Great Internet Mersenne Prime Search (GIMPS).
How to Find Prime Numbers?
The following two methods will help you to find whether the given number is a prime or not.
Method 1:
We know that 2 is the only even prime number. And only two consecutive natural numbers which are prime are 2 and 3. Apart from those, every prime number can be written in the form of 6n + 1 or 6n – 1 (except the multiples of prime numbers, i.e. 2, 3, 5, 7, 11), where n is a natural number.
For example:
6(1) – 1 = 5
6(1) + 1 = 7
6(2) – 1 = 11
6(2) + 1 = 13
6(3) – 1 = 17
6(3) + 1 = 19
6(4) – 1 = 23
6(4) + 1 = 25 (multiple of 5)
Method 2:
To know the prime numbers greater than 40, the below formula can be used.
n2 + n + 41, where n = 0, 1, 2, ….., 39
For example:
(0)2 + 0 + 0 = 41
(1)2 + 1 + 41 = 43
(2)2 + 2 + 41 = 47
Example Questions:
Example 1: Is 10 a Prime Number?
Answer – No, because it can be divided evenly by 2 or 5, 2×5=10, as well as by 1 and 10.
Example 2: Is 19 a Prime Number?
Answer – First we need to find the number k, such that k2>19.
Thus the value of k comes out to be 5, as 52 = 25.
The prime numbers less than 5 are 2 and 3.
Clearly, we can see that 19 is not divisible by both 2 and 3.
Therefore, 19 is a prime number.
Note- It should be noted that an integer suppose, P > 1 is termed as a prime number when its only divisors are 1 and P.
Any numeric m > 1 which is not a prime is termed as a composite.
Each composite number can be factored into prime factors, and individually all of these are unique in nature.
Properties of Prime Numbers
Some of the properties of primes are:- Every number greater than 1 can be divided by at least one prime number.
- Every even positive integer greater than 2 can be expressed as the sum of two primes.
- Except 2, all other prime numbers are odd. In other words, we can say that 2 is the only even prime number.
- Two prime numbers are always coprime to each other.
- Each composite number can be factored into prime factors, and individually all of these are unique in nature.
Prime Numbers and Composite Numbers
| Prime Numbers | Composite Numbers |
| A prime number has two factors only. | A composite number has more than two factors. |
| It can be divided by 1 and the number itself. For example, 2 is divisible by 1 and 2. | It can be divided by all its factors. For example, 6 is divisible by 2,3 and 6. |
| Examples: 2, 3, 7, 11, 109, 113, 181, 191, etc. | Examples: 4, 8, 10, 15, 85, 114, 184, etc. |
Prime Factorization
- Breaking down a number into its prime factors is a valuable skill on the GMAT. To create a prime factor tree, start by identifying numbers that evenly divide into the given number.
- For instance, with the number 72, test different divisors until finding one that divides without leaving a remainder.
- Once such a divisor is found, split the number into factors.
- For example, since 72 is divisible by 6, it can be split into 6 and 72 ÷ 6, which is 12. Repeat this process for 6 and 12 until each branch on the tree ends with a prime number. Continue until only prime numbers remain, as prime numbers cannot be split further. In the case of 72, it breaks down into 5 prime factors (including repeats): 2 × 3 × 2 × 2 × 3.
Factor Foundation Rule
- It states that if a is a factor of b, and b is a factor of c, then a is a factor of c as well. In simpler terms, any whole number is divisible by all its factors, and it's also divisible by the factors of those factors.
- For example, if 72 is divisible by 12, then 72 is also divisible by all the factors of 12, including 1, 2, 3, 4, 6, and 12. This rule allows you to view factors as essential building blocks forming a foundation. For instance, 12 and 6 are factors, or building blocks, of 72 because 12 × 6 equals 72.
- Moreover, the number 12 is constructed from its own factors, such as 4 × 3 building 12. Consequently, if 12 is part of the foundation of 72 and 12 is built from its prime factors (2, 2, and 3), then 72 is also constructed on the foundation of 2, 2, and 3.
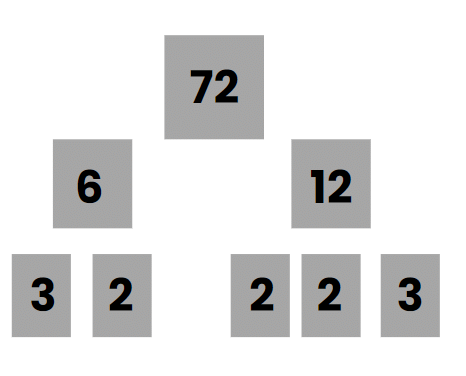
- Taking it a step further, almost any factor of 72 can be built using the bottom level of the foundation. For instance, 8 is a factor of 72 because you can create 8 using the three 2's in the bottom row (8 = 2 × 2 × 2). However, there is an exception – the number 1 cannot be constructed from the building blocks in the foundation. Despite not being prime, 1 is a factor of every integer. With this exception, every factor of 72 can be constructed using the lowest level of the building blocks in its foundation.
Division Method for Prime Factorization
The steps to calculate the prime factors of a number is similar to the process of finding the factors of a large number. Follow the below steps to find the prime factors of a number using the division method:
Step 1: Divide the given number by the smallest prime number. In this case, the smallest prime number should divide the number exactly.
Step 2: Again, divide the quotient by the smallest prime number.
Step 3: Repeat the process, until the quotient becomes 1.
Step 4: Finally, multiply all the prime factors
Example:
Prime factorization of 460.
Step 1: Divide 460 by the least prime number i.e. 2.
So, 460 ÷ 2 = 230
Step 2: Again Divide 230 with the least prime number (which is again 2).
Now, 160 ÷ 2 = 115
Step 3: Divide again with the least prime number which will be 5.
So, 115 ÷ 5 = 23
Step 4: As 23 is a prime number, divide it with itself to get 1.
Now, the prime factors of 460 will be 22 x 5 x 23
|
121 videos|148 docs|111 tests
|
FAQs on Introduction to Prime Numbers - Quantitative for GMAT
| 1. What is a prime number? |  |
| 2. How can I find prime numbers? |  |
| 3. What are the properties of prime numbers? |  |
| 4. Can prime numbers be odd or even? |  |
| 5. Are all composite numbers non-prime? |  |

















