Notes: Sets | Mathematics (Maths) Class 11 - Commerce PDF Download
Introduction to Set
- We often deal with a group or a collection of objects, such as a collection of books, a collection of English alphabets, a class of students, a list of states in a country, a collection of coins, etc.
- Set may be considered as a mathematical way of representing a collection or a group of objects.
Definition of Set
- “A set is a collection of well-defined objects.' In other words, a set is collection of defined and distinct objects. The objects of a set are called elements or members of the set. Further a set is always denoted by these brackets or braces { }.
Example: A = is a set of the letters of the word “FOLLOW’’
Then the set A will be a collection of the letters F, O, L, W.
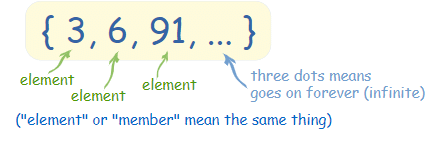
Note: Here defined means existence of elements and distinct means there is no need to write repeated elements.
- The main property of a set is that it is well defined. This means that given any object, it must be clear whether that object is a member (element) of the set or not.
Generally, sets are named with the capital letters A, B, C, etc. - The elements of a set are denoted by the small letters a, b, c, etc. and if a is an element of a set A then a ‘belongs to’ the set A where the phrase ‘belongs to’ is denoted by ∈ (which is also known as epsilon). Then we write a ∈ A. If a is not the element of A then we write a ∉ A.
Example: A is a set of natural numbers then 3 ∈ A and 0 ∉ A.
Some examples of sets in daily life are:
- Students of our classroom.
- Collection of animals of the world.
- Collection of fruits.
- Collection of vegetables.
Which of the following collection are sets? Justify your answer.
Q.1. A collection of all-natural numbers less than 50.
Ans. It forms a set. The set will have the following elements.
A = {1, 2, 3, 4, 5, ................... 49}
Q.2. A collection of good hockey players in America
Ans. It doesn't form a set. Because the term "Good player" is vague and it is not well defined. However, a collection of players of hockey is a set.
Q.3. A collection of all girls in our class.
Ans. It forms a set. The elements of the above set are the names of those girls in the class.
Q.4. A collection of prime numbers less than 30
Ans. It forms a set. The set will have the following elements.
A = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}
Q.5. A collection of ten most talented mathematics teachers.
Ans. It doesn't form a set. Because the term "Most talented" is vague and is not well defined. However, a collection of mathematics teachers is a set.
In this chapter we will have frequent interaction with some sets, so we reserve some letters for these sets as listed below:
N: The set of natural numbers
Z: The set of integers
Z+: The set of all positive integers
Q: The set of all rational numbers
Q+: The set of all positive rational numbers
R: The set of all real numbers
R+: The set of all positive real numbers
C: The set of all complex numbers
➢ How to Represent a Set?
There are two methods to represent a set:
- Roster or tabular form.
- Set builder form.
1. Roster Form
In roster form, a set is described by listing the elements, separated by commas, within the braces.
Examples:
(i) A set of vowels of English alphabets is described by {a, e, i, o, u}
(ii) A set of whole numbers is described by {1, 2, 3, 4, 5, 6,………..}
(iii) A set even natural numbers is described by {2, 4, 6, 8, 10,……..}
2. Set Builder Form
To understand set builder form we can take the help of some examples:
As discussed above, A = {a, e, i, o, u}
In set builder form, A = {x : x is a vowel of English alphabets} or {x | x is a vowel of English alphabets}
B = {1, 2, 3, 4, 5, 6,……….}
In set builder form, B = {x : x is a natural number} or {x | x is a natural number} or {x : x ∈ N} C = {2, 4, 6, 8, 10,……..}
In set builder form
C = {x : x = 2n, n ∈ N}
Note: The set of real numbers cannot be represented by roster form. In set builder form, A = {x : x ∈ R}
Different Kind of Sets
1. Empty Set or Null Set: A set containing no elements is called the empty set or null set or void set.
Reading Notation:
So, it is denoted by { } or ∅.
Example: Consider the set A = {x : x < 1, x ∈ N}
There is no natural number which is less than 1.
Therefore, A = { }, or ∅.
Note: The concept of empty set plays a key role in the study of sets just like the role of the number zero in the study of the number system.
► Cardinal Number of a Set (Order of a set)
Cardinality or order of a set is defined as the number of elements that a set has. It is denoted by n(A) or c(A) or o(A) or |A| or #A.
Example: A = {a, b, c} then n(A) = 3 and if A = { } or ∅ then n(A) = 0.
Q.1. Which of the following sets are empty?
(i) Set of counting numbers between 5 and 6.
(ii) Set of odd numbers between 7 and 19.
(iii) Set of odd numbers between 7 and 9.
(iv) Set of even numbers which are not divisible by 2.
(v) {0}
(vi) { }
(vii) {Prime numbers between 7 and 11}
(viii) {x | x ∈ N and 3< x < 4}
Ans. (i), (iii), (iv), (vi) & (viii) are empty sets.
Q.2. State, whether or not the following sets are empty:
(i) {1, 4, 7, 10, ………, 31}
(ii) {Month having more than 31 days}
(iii) {x | x2 = 0}
(iv) {x | x ∈ N and x < 1}
(v) {Prime numbers divisible by 2}
(vi) {Negative natural numbers}
(vii) {Women who are 5 meter tall}
(viii) {Men with four legs}
(ix) {Integers less than 5}
(x) {A week having 10 days}
(xi) {People who are 500 years old}
(xii) {Prime numbers between 17 and 23}
(xiii) {Set of even numbers, not divisible by 2}
(xiv) {Set of multiples of 3, which are more than 9 and less than 15}
Ans. Empty Sets: (ii), (iv), (vi), (vii), (viii), (x), (xi) & (xiii)
Not Empty Sets: (i), (iii), (v), (ix), (xii) & (xiv)
2. Finite Set: If the number of elements in a set is zero or finite, then the set is called a finite set.
Example:
(i) Consider the set A of natural numbers between 8 and 9.
There is no natural number between 8 and 9.
So, A = { } and n(A) = 0.
Hence, A is a finite set.
(ii) Consider the set X = {x : x is an integer and -1 ≤ x ≤ 2}
So, X = {-1, 0, 1, 2} and n(X) = 4
Hence, X is a finite set.
Note: The cardinal number of a finite set is finite.
3. Infinite Set: A set is said to be an infinite set if the number of elements in the set is not finite.
Example: Let W = The set of all whole numbers.
That is, W = {0, 1, 2, 3, ......................}
The set of all whole numbers contain infinite number of elements.
Hence, W is an infinite set.
Note: The cardinal number of an infinite set is not a finite number.
Q.1. State, whether the given set is infinite or finite:
(i) {3, 5, 7, ….}
(ii) {1, 2, 3, 4}
(iii) {….., -3, -2, -1, 0, 1, 2}
(iv) {20, 30, 40, 50, ………., 200}
(v) {7, 14, 21, …………, 2401}
(vi) {0}
(vii) {∅}
(viii) {x | x is an even natural number less than 10, 000}
(ix) {All people in the world}
(x) {x | x is a prime number}
(xi) {x | x ∈ N and x > 10}
(xii) {….., -2, -1, 0}
Ans. Finite Sets: (ii), (iv), (v), (vi), (vii), (viii) & (ix)
Infinite Sets: (i), (iii), (x), (xi) & (xii)
Q.2. State, whether the following set is infinite or finite:
(i) Set of integers
(ii) {Multiples of 5}
(iii) {Fractions between 1 and 2}
(iv) {Numbers of people in India}
(v) Set of trees in the world
(vi) Set of prime numbers
(vii) Set of leaves on a tree
(viii) Set of children in all the schools of Delhi}
(ix) Set of seven natural numbers
(x) {……, -4, -, 2, 0, 2, 4, 6, 8}
(xi) {-12, -9, -6, -3, 0, 3, 6, ……}
(xii) {Number of points in a line segment 4 cm long}.
Ans. Finite Sets: (iv), (vii) & (viii)
Infinite Sets: (i), (ii), (iii), (v), (vi), (ix), (x), (xi) & (xii)
Q.3. State, whether the following are finite sets, or infinite sets:
(i) {2, 4, 6, 8, …….., 800}
(ii) {-5, -4, -3, -2, …..}
(iii) {…., -5, -4, -3, -2,}
(iv) {Number of C.B.S.E. school in Delhi}
(v) {x : x is an integer between -60 and 60}
(vi) {No. of electrical appliances working in your house}
(vii) {x : x is a whole number greater than 20}
(viii) {x : x is a whole number less than 20}
Ans. Finite Sets: (i), (iv), (v), (vi) & (viii)
Infinite Sets: (ii), (iii) & (vii)
4. Singleton Set: A set containing only one element is called a singleton set.
Example: Consider the set A = {x : x is an integer and 1 < x < 3}
So, A = {2}. That is, A has only one element.
Hence, A is a singleton set.
Note: {0} is not null set. Because it contains one element. That is "0".
5. Equivalent Set: Two sets A and B are said to be equivalent if they have the same number of elements.
In other words, A and B are equivalent if n(A) = n(B).
Reading notation
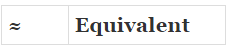
"A and B are equivalent" is written as A ≈ B
For example:
Consider A = {1, 3, 5, 7, 9} and B = {a, e, i, o, u}
Here n(A) = n(B) = 5
Hence, A and B are equivalent sets.
6. Equal Sets: Two sets A and B are said to be equal if they contain exactly the same elements, regardless of order.
Otherwise, the sets are said to be unequal.
In other words, two sets A and B are said to be equal if
(i) Every element of A is also an element of B and
(ii) Every element of B is also an element of A.
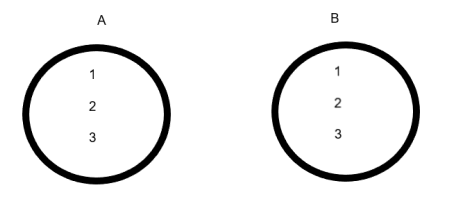 Fig: A and B are Equal Sets
Fig: A and B are Equal Sets
Reading notation:

Example: Consider A = {a, b, c, d} and B = {d, b, a, c}
Set A and set B contain exactly the same elements.
And also n(A) = n(B) = 4.
Hence, A and B are equal sets.
Note: If n(A) = n(B), then the two sets A and B need not be equal. Thus, equal sets are equivalent but equivalent sets need not be equal.
Q.1. State, if the given pairs of sets are equal sets or equivalent sets:
(a) {Natural numbers less than five} and {Letters of the word ‘BOAT’}
(b) {2, 4, 6, 8, 10} and {even natural numbers less than 12}
(c) {a, b, c, d} and {∆, ○, □, ∇}
(d) {Days of the week} and {Letters of the word ‘HONESTY}
(e) {1, 3, 5, 7, ……} and set of odd natural numbers.
(f) {Letters of the word ‘MEMBER’} and {Letters of the word ‘REMEMBER’}
(g) {Negative natural numbers} and {50th day of a month}
(h) {Even natural numbers} and {Odd natural numbers}
Ans.
(a) Equivalent
(b) Equal
(c) Equivalent
(d) Equivalent
(e) Equal
(f) Equal
(g) Equal
(h) Equivalent
Subset
A set A is a subset of set B if every element of A is also an element of B.
In symbol, we write a⊆ b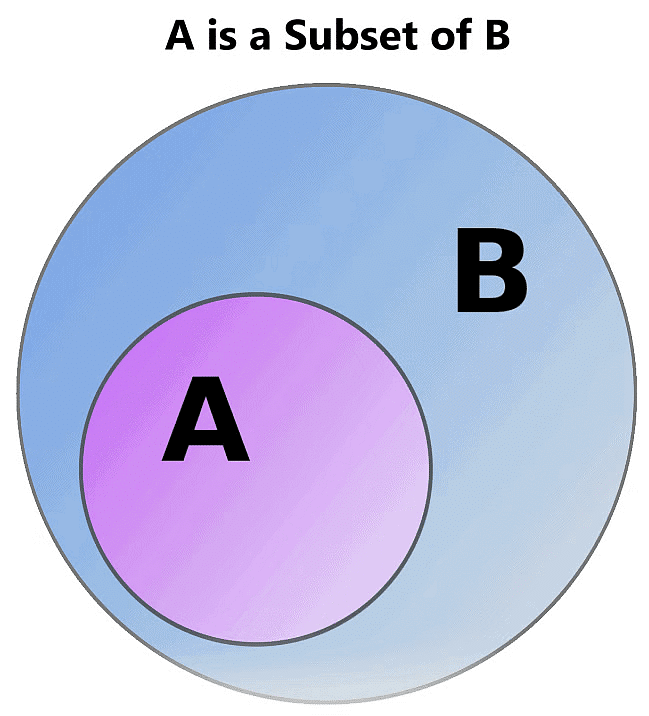 Reading Notation:
Reading Notation:
Read ⊆ as "X is a subset of Y" or "X is contained in Y"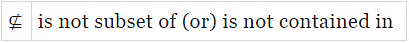
Read ⊈ as "A is a not subset of B" or "A is not contained in B".
The formula for calculating the number of subsets = 2n, where n = number of elements in the set.
Note:
- If A and B are any two non-empty sets such that A ⊆ B Let x be any element such that x ∈ A ⇒ x ∈ B
- Every set is a subset of itself that means A ⊆ A
- An empty set i.e ∅ is a subset of every set
Representation of the Subsets of Real Numbers
Intervals as subsets of R:
- Closed interval: Let a and b are two real numbers such that a < b. Then the set of all real numbers x such that a ≤ 𝑥 ≤ b is called closed interval and denoted by [a, b].
Thus [a, b] = {x : x ∈ 𝑅, a ≤ 𝑥 ≤ b}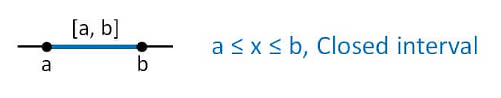
- Open interval: similarly open intervals are denoted by (a, b) where
(a, b) = {x : x ∈ 𝑅, a < 𝑥 < b }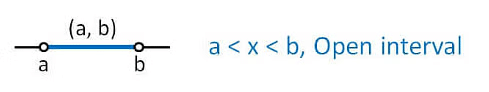
- Semi-open or semi-closed interval: here these intervals are denoted by (a, b] or [a, b)
(a, b] ={x : x∈ 𝑅, a < 𝑥 ≤ b} or [a, b) = {x : x ∈ 𝑅, a ≤ 𝑥 < b}
Example.1
Which of the following are correct statements for the following set A:
A = {1, 2, 3, 4, 5, 6}
(a) {2, 3} ⊂ A (b) {1, 2, 3, 4, 5,6, 7} ⊃ A
(c) 8 ⊂ A (d) {3, 5, 1, 7} ⊃ A
(e) {1} ⊂ A (f) {1, 2, 3, 4} ⊂ A
(g) { } ⊃ A (h) ϕ ⊂ A
Ans. (a) Since 2 and 3 are part of set A
(b) Since all elements of set A are present in {1,2,3,4,5,6,7}
(e) Since 1 is part of set A
(f) Since 1,2,3 and 4 are part of set A
(h) Since null set is part of all sets
Types of Subsets
Subsets are classified as:
- Proper Subset
- Improper Subsets
A proper subset is one that contains a few elements of the original set whereas an improper subset, contains every element of the original set along with the null set.
Example: If set A = {2, 4, 6}, then,
Number of subsets: {2}, {4}, {6}, {2,4}, {4,6}, {2,6}, {2,4,6} and Φ or {}.
Proper Subsets: {}, {2}, {4}, {6}, {2,4}, {4,6}, {2,6}
Improper Subset: {2,4,6}
1. Proper Subsets
- Set A is considered to be a proper subset of Set B if Set B contains at least one element that is not present in Set A.
- Example: If set A has elements as {12, 24} and set B has elements as {12, 24, 36}, then set A is the proper subset of B because 36 is not present in the set A.
- A proper subset is denoted by ⊂ and is read as ‘is a proper subset of’. Using this symbol, we can express a proper subset for set A and set B as:
A ⊂ B - If we have to pick n number of elements from a set containing N number of elements, it can be done in NCn number of ways.
- Therefore, the number of possible subsets containing n number of elements from a set containing N number of elements is equal to NCn.
How many subsets and proper subsets does a set have?
- If a set has “n” elements, then the number of subset of the given set is 2n and the number of proper subsets of the given subset is given by 2n - 1.
- Example: If set A has the elements, A = {a, b}, then the proper subset of the given subset are { }, {a}, and {b}. Here, the number of elements in the set is 2.
We know that the formula to calculate the number of proper subsets is 2n – 1.
= 22 – 1 = 4 – 1 = 3
Thus, the number of proper subset for the given set is 3 ({ }, {a}, {b}).
2. Improper Subset
- A subset that contains all the elements of the original set is called an improper subset. It is denoted by ⊆.
Example: Set P ={2,4,6} Then, the subsets of P are;
{}, {2}, {4}, {6}, {2,4}, {4,6}, {2,6} and {2,4,6}.
Where, {}, {2}, {4}, {6}, {2,4}, {4,6}, {2,6} are the proper subsets and {2,4,6} is the improper subsets. Therefore, we can write {2,4,6} ⊆ P.
Note: The empty set is an improper subset of itself (since it is equal to itself) but it is a proper subset of any other set.
Superset
- In set theory, set A is considered as the superset of B, if all the elements of set B are the elements of set A.
- Example: If set A = {1, 2, 3, 4} and set B = {1, 3, 4}, we can say that set A is the superset of B. As the elements of B [(i.e.,)1, 3, 4] are in set A. We can also say that B is not a superset of A.
- A set X is said to be a proper subset of set Y if X ⊆ Y and X ≠ Y.
In symbol, we write X ⊂ Y - Here, Y is called superset of X
Y ⊇ X i.e. Y is the superset of X or Y contains X.
Power Set
- The set of all subsets of A is said to be the power set of the set A.
- Reading Notation:

The power set of A is denoted by P(A) - Example: Z = {1, 3, 5}
Here, the number of the elements of Z is 3.
The subsets of Z are { }, {1}, {3}, {5}, {1, 3}, {3, 5}, {1, 5}, {1, 3, 5}
The power set of Z is the set of all the subsets of Z. We will list all the subsets then enclose them in the curly braces “{ }”
P(Z) = { { }, {1}, {3}, {5}, {1, 3}, {3, 5}, {1, 5}, {1, 3, 5} }
Hence n(P(z)) = 2𝑛, where n is the number of elements in set Z.
Universal Set
- The universal set is the super set of all the elements under consideration. If we are talking about no. of people in India, China and Japan then the universal set will be the set of all the people of these three countries.
- Example: N = {1, 2, 3, 4, 5,…}, A = {1, 3, 5, 7,…} & B = {2, 4, 6, 8,…}
Here in Set A and B we are talking about the odd numbers and even numbers so N i.e. the set of natural numbers will be the universal set of A and B. As it includes all the elements of A and B.
Practice Questions
Q1: How many elements are there in power set if
(a) A = {ϕ}
(b) B = {a, b}
(c) C = {l, m, n}
(d) D = {4, 9}
Ans.
(a) Here n(A) = 0 ,so n(P(A)) = 20 = 1
(b) Here n(B)= 2, so n(P(B))= 22= 4
(c) Here n(C)= 3, so n(P(C))= 23= 8
(d) Here n(D)=2, so n(P(D))=22= 4
Q2: Find the number of proper subsets of the following.
(a) P = {x : x ∈ N, x < 5}
(b) Q = {x : x is an even prime number}
(c) R = {x : x ∈ W, x < 2}
(d) T = { }
(e) X = {0}
(f) Y = {x : x is prime, 2 < x < 10}
Ans.
(a) Following are the elements of Set P= {1,2,3,4,}, therefore n=4
So, no. of proper subsets= 2n-1 =24-1= 15
(b) Following are the elements of Set Q={2}, therefore n=1
So, no. of proper subsets= 2n-1 =21-1= 1
(c) Following are the elements of Set R= {0,1,2}, therefore n=3
So, no. of proper subsets= 2n-1= 23-1= 7
(d) Following are the elements of Set R= {}, therefore n=0
So, no. of proper subsets= 2n-1= 20-1=0
(e) Following are the elements of Set X= {0}, therefore n=1
So, no. of proper subsets= 2n-1= 21-1=1
(f) Following are the elements of Set Y= {3,5,7}, therefore n=3
So, no. of proper subsets= 2n-1= 23-1= 7
Q3: Write down all the subsets of
(a) {8}
(b) {p, q}
(c) {1, 3, 5}
(d) ϕ
Ans.
(a) ∅, {8}
(b) ∅, {p}, {q}, {p, q}
(c) ∅, {1}, {3}, {5}, {1, 3}, {1, 5}, {3, 5}, {1, 3, 5}
(d) ∅
Q4: Fill in the blank spaces using the symbols ⊂ or ⊄.
(a) {1, 2, 3} ______ {1, 3, 5}
(b) ϕ ______ {4, 7, 9}
(c) {x : x is rectangle in a plane} ______ {x : x is a quadrilateral in a plane}
(d) {x : x is an odd natural number} ______{x : x is an integer}
(e) {x : x is a prime number} ______ {x: x is a composite number}
(f) {5, 10, 15, 20, 25, 30} ______ {10, 20, 30, 40}
Ans.
(a) ⊄
(b) ⊂
(c) ⊂
(d) ⊂
(e) ⊄
(f) ⊄
Q5: Given set A = {a, b, c) B = {p, q, r} C = {x, y, z, m, n, t} which of following are considered as universal set for all the three sets.
(a) P = {a, b, c, p, q, x, y, m, t}
(b) Q = {ϕ}
(c) R = {a, c, q, r, b, p, t, z, m, n, x, y}
(d) S = {b, c, q, r, n, t, p, q, x, m, y, z, f, g}
Ans. (c) as it contains all the elements of sets A, B & C.
Q6: Let A be the set of letters of the word FOLLOW. Find:
(a) A
(b) n(A)
(c) Number of subsets of A
(d) Number of proper subsets of A
(e) Power set of A
Ans.
(a) {F, O, L, W}, because we only consider unique elements in a set
(b) 4, that is the no. of elements in set A
(c) Since n=4 and no. of subsets= 2n
So, no. of subsets= 24=16.
(d) Since n=4 and no. of proper subsets= 2n-1
For set A, no. of proper subsets= 24-1= 15
(e) {∅, {F}, {O}, {L}, {W}, {F, O}, {F, L}, {F, W}, {O, L}, {O, W}, {L, W}, {F, O, L}, {F, O, W}, {F, L, W}, {O, L, W}, {F, O, L, W}}
Q7: Find the power set of the following sets.
(a) A = {a, b, c}
(b) B = {0, 7}
(c) C = {0, 5, 10}
(d) D = {x}
Ans.
(a) {∅, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}}
(b) {∅, {0}, {7}, {0, 7}}
(c) {∅, {0}, {5}, {10}, {0, 5}, {0, 10}, {5, 10}, {0, 5, 10}}
(d) {∅, {x}}
Introduction to Venn Diagram
A Venn diagram is a diagrammatic representation of all the possible relationships between different sets of a finite number of elements. A Venn diagram is also known as a Primary diagram, Set diagram or Logic diagram.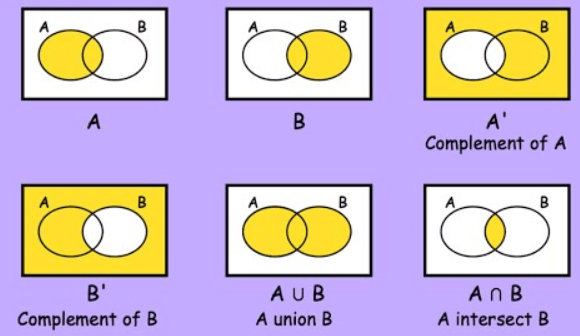
Fig: Venn Diagrams for Set A and B
Representation of Sets in a Venn Diagram
It is done as per the following:
- Each individual set is represented by a circle and enclosed within a quadrilateral (the quadrilateral represents the finiteness of the Venn diagram as well as the Universal set.)
- Labeling is done for each set with the set’s name to indicate difference and the respective constituting elements of each set are written within the circles.
- Sets having no element in common are represented separately while those having some of the elements common within them are shown with overlapping.
- The elements are written within the circle representing the set containing them and the common elements are written in the parts of circles that are overlapped.
Operations on Venn Diagrams
Just like the mathematical operations on sets like Union, Difference, Intersection, Complement, etc. we have operations on Venn diagrams that are given as follows:(i) Union of Sets
Let A = {2, 4, 6, 8} and B = {6, 8, 10, 12}. Represent A∪B through a well-labeled Venn diagram.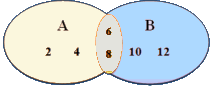
The orange colored patch represents the common elements {6, 8} and the quadrilateral represents
A ∪ B.
Properties of A U B
- The commutative law holds true as A ∪ B = B ∪ A
- The associative law also holds true as (A ∪ B) ∪ C = A ∪ (B ∪ C)
- A ∪ φ = A (Law of identity element)
- A ∪ A = A (Idempotent law)
- Law of the Universal Set - A ∪ U = U
(ii) The Intersection of Sets
An intersection is nothing but the collection of all the elements that are common to all the sets under consideration. Let A = {2, 4, 6, 8} and B = {6, 8, 10, 12} then A ∩ B is represented through a Venn diagram as per following:The orange colored patch represents the common elements {6, 8} as well as the A ∩ B. The intersection of 2 or more sets is the overlapped part(s) of the individual circles with the elements written in the overlapped parts.
Example:
Properties of A ∩ B
- Commutative law – A ∩ B = B ∩ A
- Associative law – (A ∩ B)∩ C = A ∩ (B ∩ C)
- φ ∩ A = φ
- U ∩ A = A
- A ∩ A = A (Idempotent law)
- Distributive law – A ∩ (B ∩ C) = (A ∩ B) U (A ∩ C)
(iii) Difference of Sets
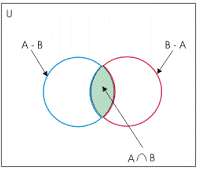
The difference of set A and B is represented as: A – B = {x : x ϵ A and x ∉ B} {converse holds true for B – A}.
Let, A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8} then,
A – B = {1, 3, 5} and B – A = {8}.
The sets (A – B), (B – A) and (A ∩ B) are mutually disjoint sets.
It means that there is NO element common to any of the three sets and the intersection of any of the two or all the three sets will result in a null or void or empty set.
Some important results
- A - B ≠ B - A
- A - B ⊆ A 𝒂𝒏d B − A ⊆ B
- A-∅ = A 𝒂𝒏d A − A = ∅
(iv) Complement of Sets
The complement of a set A is the set of all the elements which are the elements of the universal set but not the elements of the A. It is represented by symbol A' or Ac.
Mathematically, A’ = U – A
Alternatively, the complement of a set A, A’ is the difference between the universal set U and the set A. Example: Let universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and set A = {1, 3, 5, 7, 9}, then the complement of A is given as A’ = U – A = {2, 4, 6, 8, 10}

Properties Of Complement Sets
- A ∪ A’ = U
- A ∩ A’ = φ
- De Morgan’s Law – (A ∪ B)’ = A’ ∩ B’ Or (A ∩ B)’ = A’∪ B’
Let's try to prove this expression.
Left hand side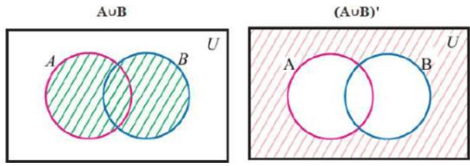
Right hand side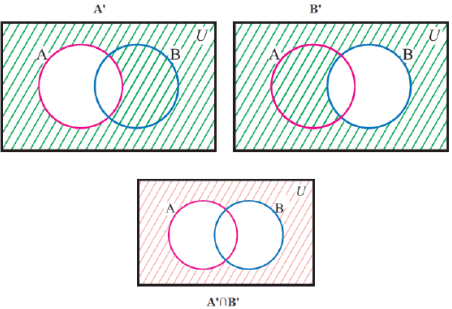
As the last image of both left hand side and the right hand side is same
Hence,this proves that (A ∪ B)’ = A’ ∩ B’.
- Double complement law : (A’)’ = A
- φ’ = U
- U’ = φ
Example
Q: Represent the Universal Set (U) = {x : x is an outcome of a dice’s roll} and set A = {s : s ϵ Even numbers} through a Venn diagram.Ans. Since, U = {1, 2, 3, 4, 5, 6} and A = {2, 4, 6}. Representing this with a Venn diagram we have:
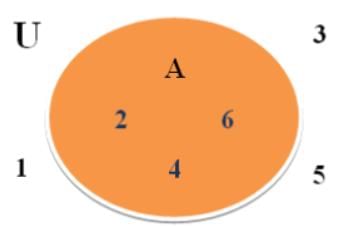
Here, A is a subset of U, represented as – A ⊂ U or
U is the super set of A, represented as – U ⊃ A
If A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7, 8}, then represent A – B and B – A through Venn diagrams.
A – B = {1, 2, 3}
B – A = {6, 7, 8}
Representing them in Venn diagrams:
a. A-B b. B-A
b. B-A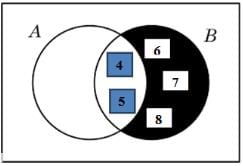
Operations on Sets
When two or more sets are combined together to form another set under some given conditions, then operations on sets are carried out.
The important operations on sets are:
(i) Union
Let X and Y be two sets.Now, we can define the following new set.
X ∪ Y = {z | z ∈ X or z ∈ Y}
(That is, z may be in X or in Y or in both X and Y)
X ∪ Y is read as "X union Y"
Now that X ∪ Y contains all the elements of X and all the elements of Y and the figure given below illustrates this.It is clear that X ⊆ X ∪ Y and also Y ⊆ X ∪ Y
(ii) Intersection
Let X and Y be two sets.Now, we can define the following new set.
X ∩ Y = {z | z ∈ X and z ∈ Y}
(That is z must be in both X and Y)
X ∩ Y is read as "X intersection Y"
Now that X ∩ Y contains only those elements which belong to both X and Y and the figure given below illustrates this.It is trivial that that X ∩ Y ⊆ X and also X ∩ Y ⊆ Y
(iii) Set difference
Let X and Y be two sets.Now, we can define the following new set.
X\Y = {z | z ∈ X but z ∉ Y}
(That is z must be in X and must not be in Y)
X\Y is read as "X difference Y"
Now that X\Y contains only elements of X which are not in Y and the figure given below illustrates this.
Some authors use A - B for A\B. We shall use the notation A \ B which is widely used in mathematics for set difference.
(iv) Symmetric difference
Let X and Y be two sets.Now, we can define the following new set.
X Δ Y = (X\Y) ∪ (Y\X)
X Δ Y is read as "X symmetric difference Y"
Now that X Δ Y contains all elements in X∪Y which are not in X∩Y and the figure given below illustrates this.
(v) Complement
If X ⊆ U, where U is a universal set, then U\X is called the compliment of X with respect to U.
If underlying universal set is fixed, then we denote U\X by X' and it is called compliment of X.
X' = U\X The difference set set A\B can also be viewed as the compliment of B with respect to A.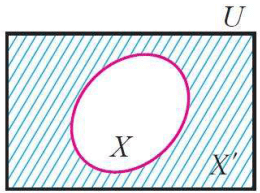
That means if x ∈ A ⇒ x ∉ A’ and x ∈ A’ ⇒ x ∉ A
(vi) Disjoint sets
Two sets X and Y are said to be disjoint if they do not have any common element. That is, X and Y are disjoint if X ∩ Y = ϕIt is clear that n(A ∪ B) = n(A) + n(B), if A and B are disjoint finite set.If A and B are not disjoint, then
(i) n ( A ∪ B) = n (A) + n (B) - n ( A ∩ B)
(ii) n(A ∪ B) = n(A - B) + n(B - A) + n(A ∩ B)
(iii) n (A) = n (A - B) + n ( A ∪ B)
(iv) n (B) = n (B - A ) + n ( A ∪ B)
If there three sets A,B and C then
𝑛(A ∪ B ∪ C) = 𝑛(A) + 𝑛(B) + 𝑛(C) − 𝑛(A ∩ B) − 𝑛(B ∩ C) − 𝑛(C ∩ A) + 𝑛(A ∩ B ∩ C)
Note: But students are advised to do questions having three sets with venn diagram
Some Important Results
- A - B = A ∩ Bc where Bc is complement of B
- (A - B) ∪ B = A ∪ B
- (A - B) ∩ B = ∅
- A ⊆ B ⇔ Bc ⊆ Ac
- A - B = Bc − Ac
|
73 videos|264 docs|91 tests
|
FAQs on Notes: Sets - Mathematics (Maths) Class 11 - Commerce
| 1. What is a subset? |  |
| 2. What is a superset? |  |
| 3. What is a power set? |  |
| 4. What is a universal set? |  |
| 5. How are sets represented in a Venn diagram? |  |

















