Introduction to Structure of Arguments | Logical Reasoning for UGC NET PDF Download
| Table of contents |

|
| Introduction |

|
| Identifying Arguments |

|
| Arguments - Types of Reasoning |

|
| Validity |

|
| Soundness |

|
| Inductive Reasoning |

|
| Good Arguments |

|
Introduction
- The story of Newton and the falling apple illustrates how knowledge can be made explicit. While apples had always fallen towards the Earth, Newton's insight transformed this implicit knowledge into a formal theory: the Universal Law of Gravitation.
- Knowledge plays a crucial role in clarifying theories. Reasoning becomes important because many problems in life are not directly solved; instead, we work towards their solutions. Different perspectives on a theory contribute to progress.

- The relationship between theories and practice is complex. Changes occur in both directions, often without our conscious awareness. Justifications for arguments should be public and objective, as private justifications are not accepted in the realm of nature.
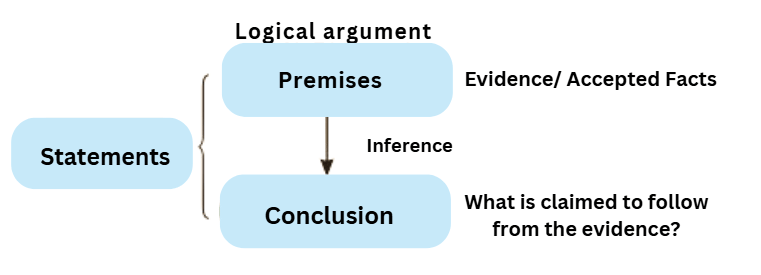
- Arguments are a series of connected statements aimed at proving a conclusion. They consist of premises and a conclusion, with premises serving as the basis for the argument. The words statements and propositions are used interchangeably with premise.
- Arguments are inferential, meaning they aim to deduce something. The conclusion of an argument is also known as an inference. For example, in an argument with multiple premises, the immediate inference supports the conclusion.
Argument: An Overview
- An argument is a connected series of statements, including one or more premises, aimed at demonstrating the truth of another statement, known as the conclusion. Arguments provide proof for a claim, and the statements that serve as premises and conclusions are often referred to as "propositions."
- A premise is a statement that leads to the conclusion of an argument. There can be one, two, or many premises in a single argument. In this context, the terms "statements" and "propositions" are used instead of "premise."
- A conclusion is the statement that is reasoned or inferred from the premises of the argument. Arguments are inferential in nature, meaning they aim to infer something. A conclusion is also known as an inference.
- Example of Argument Structure:Arguments often consist of two or more premises. The immediate inference involves a single premise that supports the conclusion. For example:
- Premise: No items on the menu are vegetable dishes.
- Conclusion: Therefore, no vegetable dishes are items on the menu.
Identifying Arguments
Signal words in text help indicate arguments. For instance, the word "because" signals that a premise or reason is being provided to support a claim.
- Value Claims: These claims involve judgments about the worth or importance of something. For example, saying "Exercise is essential for a healthy lifestyle" reflects a value judgment about the importance of exercise.
- Policy Claims: These claims advocate for a specific course of action or policy. For instance, arguing that "The government should implement stricter environmental regulations" suggests a particular policy direction.
- Factual Claims: These claims assert something as a fact, which can be proven or disproven. For example, stating "Climate change is caused by human activities" presents a factual assertion.
Examples of words and phrases that may signal a premise include as, due to, as indicated by, for the reason that, owing to, through, in the view of, and as a result of.
The word "therefore" and its synonyms are clues that a conclusion or claim is being made. Other words that signal a conclusion include accordingly, consequently, infer that, hence, prove that, and conclude that.
For instance, consider the argument "The internet is a good invention." This claim can be supported with reasons like "It is a source of endless information" and "It is a hub of entertainment." Finally, a conclusion wraps up the argument.
Arguments - Types of Reasoning
Deductive Reasoning
Deductive reasoning is a logical process where a conclusion is drawn from a set of premises with certainty. It involves starting with general statements and applying them to specific instances. Let's explore this concept further.
In deductive reasoning, the conclusion is a necessary outcome of the premises. For example, consider the following premises:
Premise 1: All humans are mortal.
Premise 2: I am a human.
Conclusion: Therefore, I am mortal.
In this example, the conclusion is logically derived from the premises. Deductive reasoning can involve multiple premises, and there is no strict limit to the number of premises that can be used to reach a conclusion. For instance, instead of just "I," we could have "you," "he," "she," and so on, making the premises more specific.
Deductive reasoning is often considered more scientific and is associated with formal logic, which is the "science of deduction." It is deterministic, meaning that the conclusion follows necessarily from the premises without exception.
Deductive inference can be further categorized into immediate and mediate reasoning:
Immediate Reasoning: This involves drawing a conclusion from a single statement.
Mediate Reasoning: This involves drawing a conclusion from two statements, known as syllogism. Syllogism will be discussed in more detail later.
Deductive reasoning is akin to analysis, where a whole is separated into its constituent elements. It is a systematic and rigorous approach to drawing conclusions based on established premises. 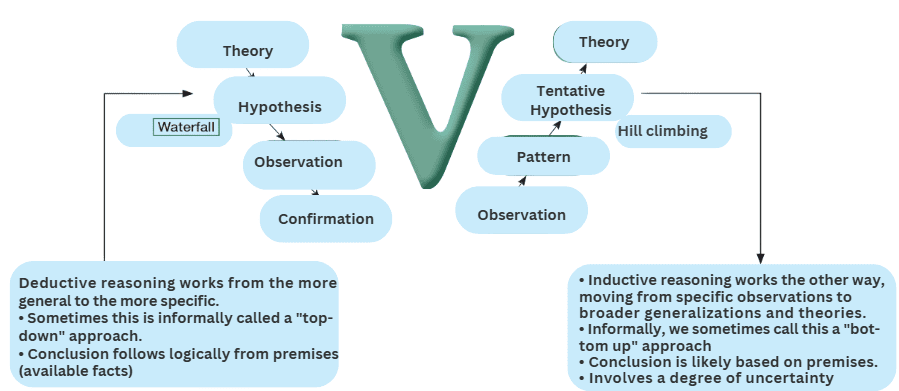 Deductive Reasoning vs Inductive Reasoning
Deductive Reasoning vs Inductive Reasoning
Validity
Validity refers to the logical strength of deductive arguments, indicating how well the premises support the conclusion. A deductive argument is considered valid when, if all its premises are true, the conclusion must also be true by necessity.
- Validity is concerned with the strength of the inference or reasoning between the premises and the conclusion.
- An argument is valid if assuming the premises are true leads to the conclusion being true as well.
- To determine the validity of an argument:
- Assume the premises are true, regardless of their actual truth.
- Check if the conclusion must be true based on the premises.
- A valid argument has the correct form, while an invalid argument does not.
Example of Validity
Consider the following argument:
- Premise 1: All dogs are dragons.
- Premise 2: All dragons are birds.
- Conclusion: All dogs are birds.
This argument is valid because if the premises were true, the conclusion would necessarily follow. Validity is determined by the form of the argument, not the truth of the premises.
Valid Arguments Can Have
- True premises and a true conclusion.
- False premises and a false conclusion.
- False premises and a true conclusion.
However, valid arguments can never have true premises and a false conclusion. In a valid deductive argument, if the premises are true, the conclusion cannot be false.
Example of Invalid Argument
Consider the following argument:
- Premise 1: All dogs are animals.
- Premise 2: All collies are animals.
- Conclusion: All collies are dogs.
In this case, the premises are true, and the conclusion is also true, but the reasoning from the premises to the conclusion is not valid. The conclusion does not necessarily follow from the premises, making the argument invalid.
Soundness
Soundness in deductive arguments refers to the combination of valid reasoning and true premises. A deductive argument is considered sound when it meets two criteria:
- Validity: The argument must be valid, meaning that the conclusion follows logically from the premises.
- Truth of Premises: All the premises in the argument must be true.
Example of Sound Argument
Consider the following argument:
- Premise 1: All cats are mammals.
- Premise 2: All mammals are animals.
- Conclusion: All cats are animals.
This argument is sound because:
- It is valid, as the premises support the conclusion by necessity.
- All of the premises are true.
Distinction from Validity
It is important to note that while all sound arguments are valid, not all valid arguments are sound. Validity only considers the logical structure of the argument, while soundness takes into account the truth of the premises as well.
For instance, the earlier example with dogs, dragons, and birds is valid because the form of the argument is correct. However, it is not sound because the premises are not true.
Inductive Reasoning
Inductive reasoning is a method of reasoning that involves drawing general conclusions from specific observations or instances. It is often used in the fields of informal logic and critical thinking, particularly in social sciences. 
Understanding Inductive Reasoning
- Inductive reasoning is about making generalizations based on specific examples.
- While it may not be 100% accurate, it is a quick way to make decisions, especially when time is a factor.
- Inductive arguments can be strong or weak based on the likelihood of the conclusion being true if the premises are assumed to be true.
Inductive strength refers to the strength of an inductive argument. An argument is inductively strong if, assuming the premises are true, the conclusion is likely to be true as well.
Determining Inductive Strength
To assess whether an inductive argument is strong or weak, follow these steps:
- Assume the premises are true, even if they are not.
- Evaluate the likelihood of the conclusion being true based on the assumed premises.
Example of Inductive Strength:
- Premise 1: Most peacocks eat oats.
- Premise 2: This bird is a peacock.
- Conclusion: Thus, this bird probably eats oats.
In this example, the argument is inductively strong because if the premises are true, the conclusion is highly likely to be true as well.
Inductive Arguments and Their Characteristics
- Inductively strong arguments can have:
- True premises and a true conclusion.
- False premises and a false conclusion.
- False premises and a true conclusion.
- Inductively strong arguments cannot have:
- True premises and a false conclusion.
In summary, a strong inductive argument makes it unlikely for the conclusion to be false if the premises are true. Conversely, a weak inductive argument suggests that the conclusion is unlikely to follow from the premises, assuming they are true.
Cogency
Cogency refers to the quality of an inductive argument based on the truth of its premises and its logical strength. An inductive argument is considered cogent when it meets the following criteria:
- Inductive Strength: The argument is inductively strong, meaning that if the premises are true, the conclusion is likely to be true.
- Truth of Premises: All premises of the argument are true.
Example of Cogency:
- Premise 1: Europa has an atmosphere containing oxygen.
- Premise 2: Oxygen is required for life.
- Conclusion: Thus, there may be life on Europa.
In this example, the argument is cogent because:
- It is inductively strong, as the conclusion is likely true if the premises are true.
- The premises are actually true.
On the other hand, an argument may demonstrate inductive strength without being cogent if it lacks true premises. For instance, the peacock example used earlier is not cogent because it does not have all true premises.
In summary, an inductive argument is cogent when it is improbable for the conclusion to be false given the truth of the premises. Cogency combines the strength of the argument with the truth of its premises to establish a compelling case.
Good Arguments
The key takeaway regarding the attributes of deductive and inductive arguments is that a good argument proves its conclusion and possesses two essential features:
- It is logically strong.
- All of its premises are true.
Logical Strength
Logical strength refers to the level of support that the premises, if true, provide for the conclusion. This characteristic is relevant to both deductive arguments (through validity) and inductive arguments (through inductive strength).
- A strong deductive argument is not only valid but also sound.
- A strong inductive argument is not only inductively strong but also cogent.
For example, consider David Hume's question, "Will the Sun rise tomorrow?" While the laws of nature suggest it will, there is still uncertainty about the future.
Let's explore examples of deductive and inductive arguments:
Deductive Reasoning
- Proposition I: All vegetables contain vitamins.
- Proposition II: Carrot is a vegetable.
- Conclusion: Thus, carrot contains vitamins.
Inductive Reasoning
- Proposition I: Most vegetables contain vitamins.
- Proposition II: Carrot is a vegetable.
- Conclusion: Thus, carrot contains vitamins.
Logical reasoning is a fundamental aspect of human thought, but humans are not always purely logical reasoners. The deductive method leads to definitive accept or reject decisions, while the inductive method results in tentative conclusions that may seem subjective. Inductive and deductive theorizing are complementary stages in constructing any theory, with induction preceding deduction.
According to Aristotle, the distinction between deductive and inductive arguments lies not in the words used but in the intentions of the arguer. If the intentions of the arguer are unknown, both aspects are assessed. This involves evaluating whether the argument is deductively valid and inductively strong.
Priori and Posteriori Arguments
- Priori Argument: A priori arguments are formed prior to sense experience, thus the term 'priori.'
- Posteriori Argument: Posteriori arguments, such as those in the context of enlightenment or new enlightenment, are derived only after sense experience has occurred.
Types of Syllogism
Syllogism, based on propositions, can be categorized into four types:
- Categorical Syllogism: In categorical syllogism, the relationship between the subject and predicate is unconditional. For example:
- Hypothetical Syllogism: The relationship between the subject and predicate is asserted conditionally. For instance, "If it rains, he will not attend."
- Disjunctive Syllogism: In a disjunctive proposition, the assertion involves alternation. For example, "Either he is courageous or he is strong."
- Relational Syllogism: Relational syllogism shows the relationship between various terms in a specific order. For example, "a > b > c > d; therefore, a > d (conclusion)."
Categorical Syllogism focuses on categorical relationships. There are exactly 256 distinct forms of categorical syllogism, derived from:
- Four kinds of major premises.
- Four kinds of minor premises.
- Four kinds of conclusions.
- Four relative positions of the middle term.
|
31 videos|44 docs|14 tests
|
FAQs on Introduction to Structure of Arguments - Logical Reasoning for UGC NET
| 1. What is the definition of an argument in logic? |  |
| 2. What are the main forms of an argument? |  |
| 3. What is a categorical proposition and how is it structured? |  |
| 4. What are the properties of a categorical proposition? |  |
| 5. What is a categorical syllogism, and how does it relate to the classical square of opposition? |  |
















