Year 10 Exam > Year 10 Notes > Mathematics for GCSE/IGCSE > Introduction to Vectors
Introduction to Vectors | Mathematics for GCSE/IGCSE - Year 10 PDF Download
Basic Vectors
What are vectors?
- A vector is a type of number that has both a size and a direction.
- We focus on two-dimensional vectors, although vectors can exist in any number of dimensions.
Representing vectors
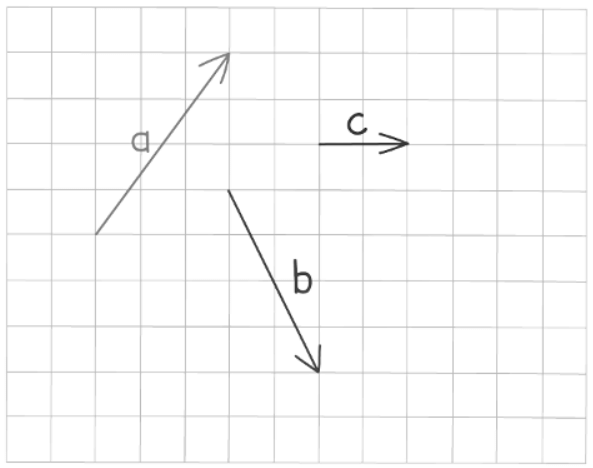
- Vectors are represented as arrows, where the arrowhead shows the direction and the length of the arrow indicates the vector's magnitude (size).
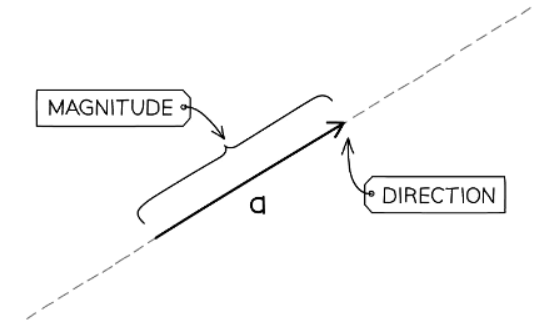
- In print vectors are usually represented by bold letters (as with vector a in the diagram above), although in handwritten workings underlined letters are normally used, a.
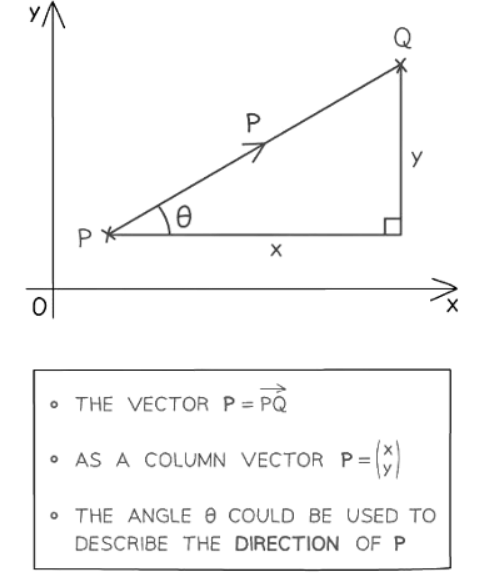
- Another way to indicate a vector is to write its starting and ending points with an arrow symbol over the top such as stack
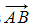
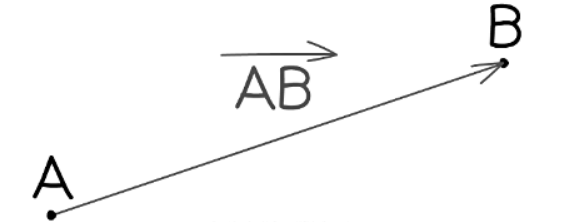
- Note that the order of the letters is important! Vector stack
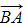 with rightwards arrow on top in the above diagram would point in the opposite direction (ie with its ‘tail’ at point B, and the arrowhead at point A).
with rightwards arrow on top in the above diagram would point in the opposite direction (ie with its ‘tail’ at point B, and the arrowhead at point A).
Vectors in Transformation Geometry
In transformation geometry, translations are represented using column vectors.
- In the following diagram, Shape A has been translated six squares to the right and 3 squares up to create Shape B
- This transformation is indicated by the translation vector
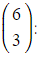
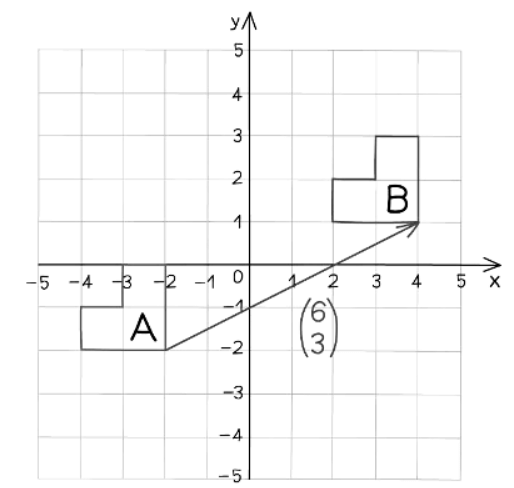
- Note: ‘Vector’ is a word from Latin that means ‘carrier’
- In this case, the vector ‘carries’ shape A to shape B, so that meaning makes perfect sense!
Vectors on a grid
- Proficiency with vectors extends beyond transformation geometry and encompasses various applications in physics, engineering, and mathematics.
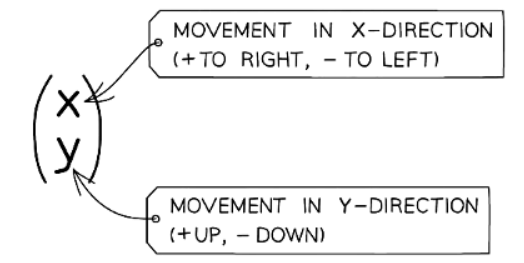
- On a grid, whether or not x and y axes are present, vectors can still be represented in the column vector form (x y).
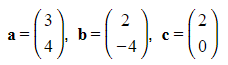
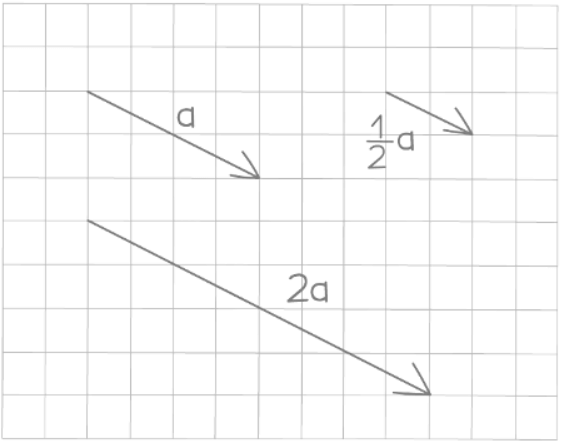
Multiplying a vector by a scalar
- Scalars are numerical quantities that possess magnitude but lack direction, unlike vectors.
- Multiplying a vector by a positive scalar alters its magnitude while preserving its direction.
- In the representation of a vector as a column vector, each element within the column vector is multiplied by the scalar when scalar multiplication is performed.
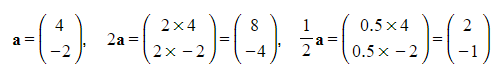
- Note that multiplying by a negative scalar also changes the direction of the vector:
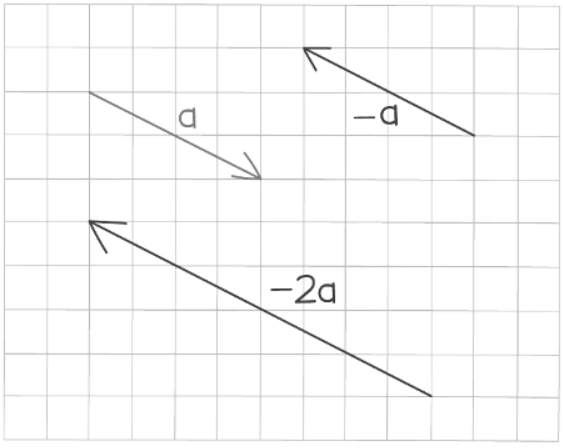
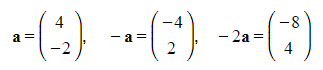
Adding and subtracting vectors
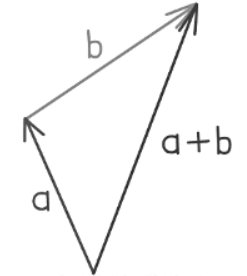
- Adding two vectors is defined geometrically, like this:
- Subtracting one vector from another is equivalent to adding the negative of the second vector to the first vector.
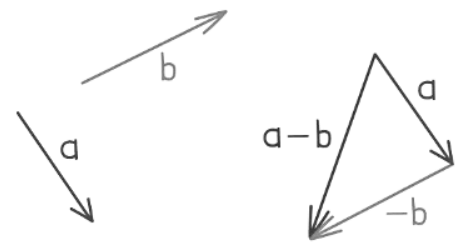 a - b = a + (-b)
a - b = a + (-b)
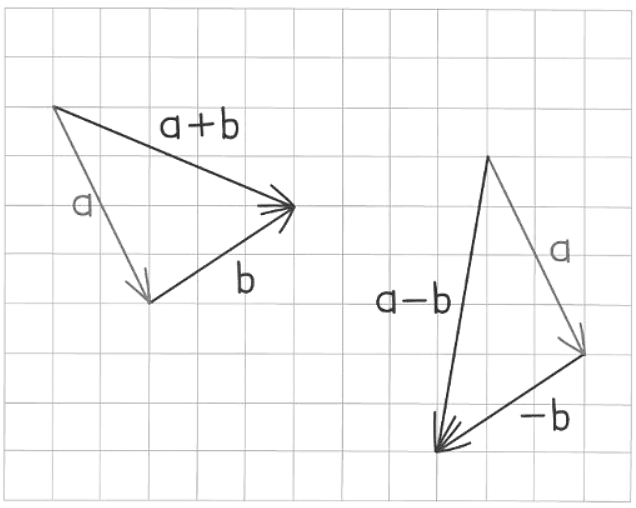
- When vectors are represented as column vectors, performing addition or subtraction involves simply adding or subtracting the corresponding x and y coordinates of the vectors.
- For example:
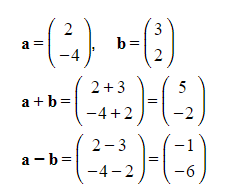
Magnitude of a Vector
What is a vector?
- Vectors serve multiple purposes in mathematics. In mechanics, they represent quantities like velocity, acceleration, and forces. In geometry, such as in the IGCSE curriculum, vectors are applied to concepts like translation.
- Familiarity with fundamental vector operations is essential, including determining magnitude or modulus, often represented in column vector form.
What is the magnitude or modulus of a vector?
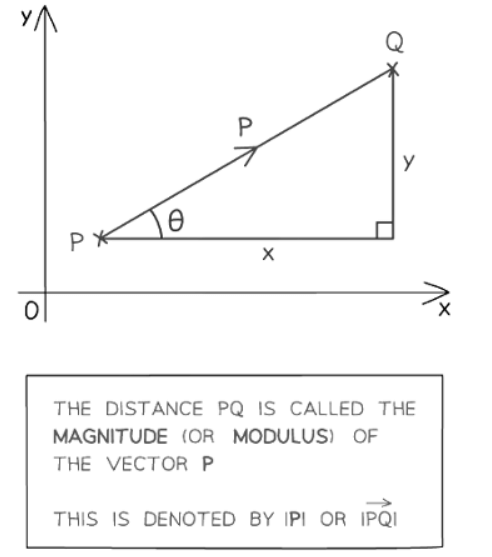
- The magnitude of a vector varies depending on its application.
- For velocity, magnitude corresponds to speed.
- In the context of force, magnitude denotes the strength of the force, typically measured in Newtons.
- The terms "magnitude" and "modulus" are synonymous when referring to vectors.
- In geometry, magnitude or modulus represents the distance of the vector, always yielding a positive value.
- The vector's direction is insignificant when determining magnitude.
- Magnitude or modulus is denoted by vertical lines, such as |a| indicating the magnitude of vector a.
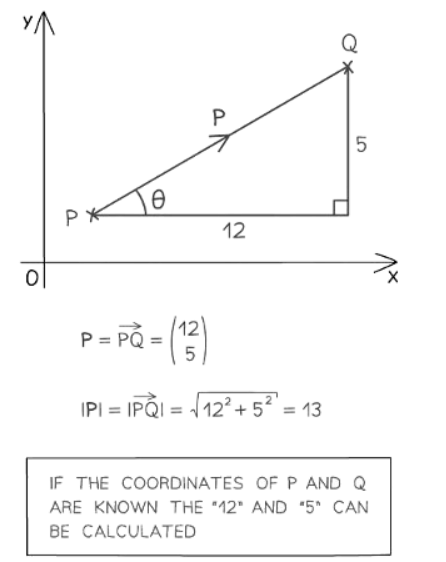
How do I find the magnitude or modulus of a vector
- Pythagoras’ Theorem!
The document Introduction to Vectors | Mathematics for GCSE/IGCSE - Year 10 is a part of the Year 10 Course Mathematics for GCSE/IGCSE.
All you need of Year 10 at this link: Year 10
|
75 videos|394 docs|60 tests
|
FAQs on Introduction to Vectors - Mathematics for GCSE/IGCSE - Year 10
| 1. What is the magnitude of a vector? |  |
Ans. The magnitude of a vector is a scalar value that represents the length or size of the vector. It is calculated using the Pythagorean theorem in two or three dimensions.
| 2. How is the magnitude of a vector represented mathematically? |  |
Ans. The magnitude of a vector is denoted by ||v||, where v is the vector. It is calculated as the square root of the sum of the squares of the vector components.
| 3. How do you find the magnitude of a vector in two dimensions? |  |
Ans. In two dimensions, the magnitude of a vector (v) with components (a, b) can be found using the formula ||v|| = sqrt(a^2 + b^2).
| 4. What is the significance of the magnitude of a vector in physics and engineering? |  |
Ans. The magnitude of a vector is crucial in determining the strength, speed, or force of physical quantities in physics and engineering. It helps in understanding the overall impact or intensity of a vector quantity.
| 5. Can the magnitude of a vector be negative? |  |
Ans. No, the magnitude of a vector is always a positive scalar value, representing the length or size of the vector. Negative values are associated with the direction of the vector, not its magnitude.
Related Searches
















