Irodov Solutions: Electric Current - 3 - Airforce X Y / Indian Navy SSR PDF Download
Q. 184. Find a potential difference φA — φB between the plates of a capacitor C in the circuit shown in Fig. 3.47 if the sources have emf's 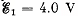 and
and 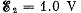 and the resistances are equal to R1 = 10 Ω, R2 = 20 Ω, and R3 = 30 Ω. The internal resistances of the sources are negligible.
and the resistances are equal to R1 = 10 Ω, R2 = 20 Ω, and R3 = 30 Ω. The internal resistances of the sources are negligible.
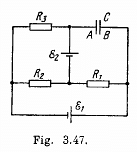
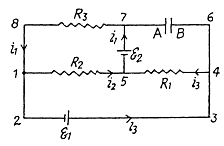
Solution. 184. Indicate the currents in all the branches using charge conservation as shown in the figure. Applying the loop rule (- Δ φ = 0) in the loops 12341 and 15781, we get
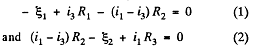
Solving Eqs. (1) and (2), we get
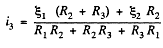
Hence, the sought p.d.
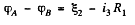
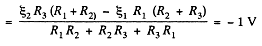
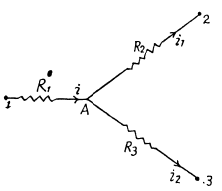
Q. 185. Find the current flowing through the resistance R1 of the circuit shown in Fig. 3.48 if the resistances are equal to R1 = 10 Ω, R2 = 20 Ω, and R3 = 30 Ω, and the potentials of points 1, 2, and 3 are equal to φ1 = 10 V, φ2 = 6 V, and φ3 = 5 V
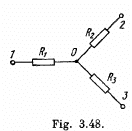
Solution. 185. Let us distribute the currents in the paths as shown in the figure.
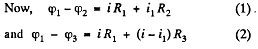
Simplifying Eqs. (1) and (2) we get
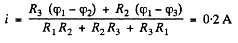
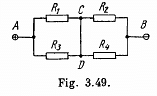
Q. 186. A constant voltage V = 25 V is maintained between points A and B of the circuit (Fig. 3.49). Find the magnitude and direction of the current flowing through the segment CD if the resistances are equal to R1 = 1.0 Ω, R2 = 2.0 Ω, R3 = 3.0 Ω, and R4 = 4.0 Ω.
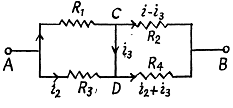
Solution. 186. Current is as shown. From Kirchhoffs Second law
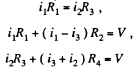
Eliminating i2
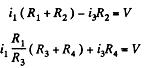
Hence
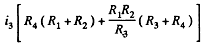
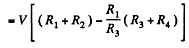
or, 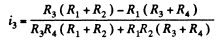
On substitution we get i3 = 1.0 A from C to D
Q. 187. Find the resistance between points A and B of the circuit shown in Fig. 3.50.

Solution. 187. From the symmetry of the problem, current flow is indicated, as shown in the figure.
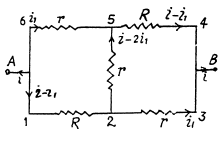
Equivalent resistance between the terminals A and B using (1) and (2),

Q. 188. Find how the voltage across the capacitor C varies with time t (Fig. 3.51) after the shorting of the switch Sw at the moment t = 0.
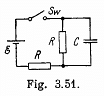
Solution. 188. Let, at any moment of time, charge on the plates be +qr and - q respectively, then voltage across the capacitor, φ = q/C (1)
Now, from charge conservation,
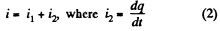
In the loop 65146, using - Δ φ • 0.
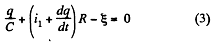
[using (1) and (2)]
In the loop 25632, using - Δ φ = 0

From (1) and (2),
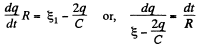 (5)
(5)
On integrating the expression (5) between suitable limits,
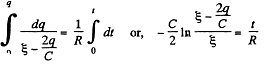
Thus 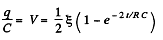
Q. 189. What amount of heat will be generated in a coil of resistance R due to a charge q passing through it if the current in the coil
(a) decreases down to zero uniformly during a time interval Δt;
(b) decreases down to zero halving its value every Δt seconds?
Solution. 189. (a) As current i is linear function of time, and at t = 0 and Δt, it equals i0 and zero respectively, it may be represented as,
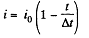
Thus 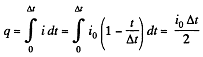
So, 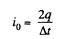
Hence, 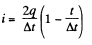
The heat generated.
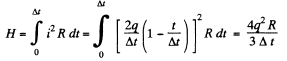
(b) Obviously the current through the coil is given by
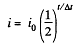
Then charge 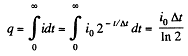
So, 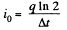
And hence, heat generated in the circuit in the time interval t [0, ∞],
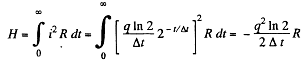
Q. 190. A de source with internal resistance R0 is loaded with three identical resistances R interconnected as shown in Fig. 3.52. At what value of R will the thermal power generated in this circuit be the highest?
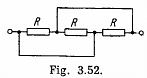
Solution. 190. The equivalent circuit may be drawn as in the figure.
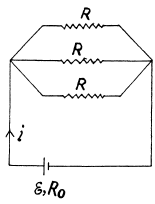
Resistance o f the network 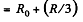
Let, us assume that e.m.f. of the cell is then current
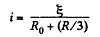
Now, thermal power, generated in the circuit

Q. 191. Make sure that the current distribution over two resistances R1 and R2 connected in parallel corresponds to the minimum thermal power generated in this circuit.
Solution. 191. We assume current conservation but not KirchhofTs second law. Then thermal power dissipated is
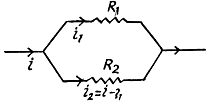

The resistances being positive we see that the power dissipated is minimum when
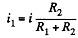
This corresponds to usual distribution of currents over resistance joined is parallel.
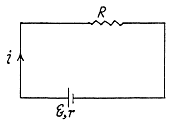
Q. 192. A storage battery with emf 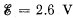 loaded with an external resistance produces a current I = 1.0 A. In this case the potential difference between the terminals of the storage battery equals V = 2.0 V. Find the thermal power generated in the battery and the power developed in it by electric forces.
loaded with an external resistance produces a current I = 1.0 A. In this case the potential difference between the terminals of the storage battery equals V = 2.0 V. Find the thermal power generated in the battery and the power developed in it by electric forces.
Solution. 192. Let, internal resistance of the cell be r, then
 (1)
(1)
where i is the current in the circuit. We know that thermal power generated in the battery.
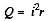
Putting r from (1) in (2), we obtain,
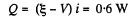
In a battery work is done by electric forces (whose origin lies in the chemical processes going on inside the cell). The work so done is stored and used in the electric circuit outside. Its magnitude just equals the power used in the electric circuit We can say that net power developed by the electric forces is
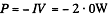
Minus sign means that this is generated not consumed.
Q. 193. A voltage V is applied to a de electric motor. The armature winding resistance is equal to R. At what value of current flowing through the winding will the useful power of the motor be the highest? What is it equal to? What is the motor efficiency in this case?
Solution. 193. As far as motor is concerned the power delivered is dissipated and can.be represented by a load, R0 . Thus
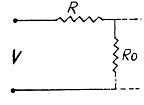
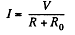
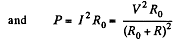
This is maximum when R0 = R and the current / is then
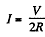
The maximum power delivered is
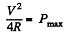
The power input is 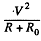 and its value when P is maximum is
and its value when P is maximum is 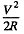
The efficiency then is 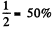
Q. 194. How much (in per cent) has a filament diameter decreased due to evaporation if the maintenance of the previous temperature required an increase of the voltage by η = 1.0%? The amount of heat transferred from the filament into surrounding space is assumed to be proportional to the filament surface area.
Solution. 194. If the wire diameter decreases by δ then by the information given
P = Power input 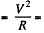 heat lost through the surface, H.
heat lost through the surface, H.
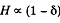 like the surface area and
like the surface area and
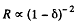
So, 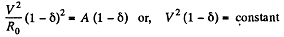
But 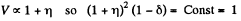
Thus 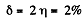
Q. 195. A conductor has a temperature-independent resistance R and a total heat capacity C. At the moment t = 0 it is connected to a de voltage V. Find the time dependence of a conductor's temperature T assuming the thermal power dissipated into surrounding space to vary as q = k (T — T0), where k is a constant, T0 is the environmental temperature (equal to the conductor's temperature at the initial moment)
Solution. 195. The equation of heat balance is
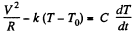
Put 
So, 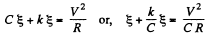
or, 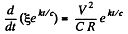
or, 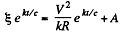
where A is a constant. Clearly
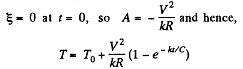
Q. 196. A circuit shown in Fig. 3.53 has resistances R1 = 20Ω and R2 = 30 Q. At what value of the resistance Rx will the thermal power generated in it be practically independent of small variations of that resistance? The voltage between the points A and B is supposed to be constant in this case.
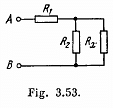
Solution. 196. 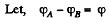
Now, thermal power generated in the resistance Rx,
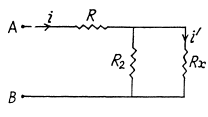
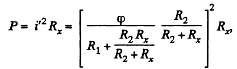
For P to be independent of Rx,
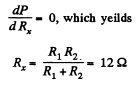
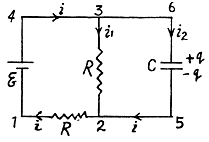
Q. 197. In a circuit shown in Fig. 3.54 resistances R1 and R2 are known, as well as emf's 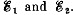 The internal resistances of the sources are negligible. At what value of the resistance R will the thermal power generated in it be the highest? What is it equal to?
The internal resistances of the sources are negligible. At what value of the resistance R will the thermal power generated in it be the highest? What is it equal to?
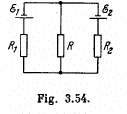
Solution. 197. Indicate the currents in the circuit as shown in the figure. Appying loop rule in the closed loop 12561, - Δφ = 0 we get

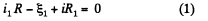
and in the loop 23452,
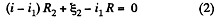
Solving (1) and (2), we get,

So, thermal power, generated in the resistance R,
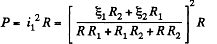
For P to be maximum, 

Hence, 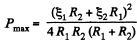
Q. 198. A series-parallel combination battery consisting of a large number N = 300 of identical cells, each with an internal resistance r = 0.3 Ω, is loaded with an external resistance R = 10 Ω. Find the number n of parallel groups consisting of an equal number of cells connected in series, at which the external resistance generates the highest thermal power.
Solution. 198. Let, there are x number of cells, connected in series in each of the n parallel groups
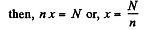 (1)
(1)
Now, for any one of the loop, consisting of x cells and the resistor R, from loop rule

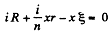
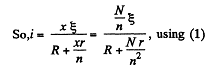
Heat generated in the resistor R,
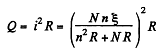 (2)
(2)
and for (2 to be maximum, 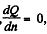 which yields
which yields
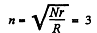
Q. 199. A capacitor of capacitance C = 5.00 µF is connected to a source of constant emf 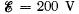 (Fig. 3.55). Then the switch Sw was thrown over from contact 1 to contact 2. Find the amount of heat generated in a resistance R1 = 500 Ω if R2 = 330 Ω.
(Fig. 3.55). Then the switch Sw was thrown over from contact 1 to contact 2. Find the amount of heat generated in a resistance R1 = 500 Ω if R2 = 330 Ω.

Solution. 199. When switch 1 is closed, maximum chaige accumulated on the capacitor,
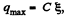 (1)
(1)

and when switch 2 is closed, at any arbitrary instant of time,
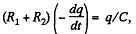
because capacitor is discharging.
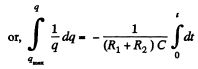
Integrating, we get
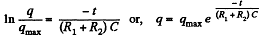 (2)
(2)
Differentiating with respect to time,
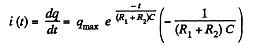
or, 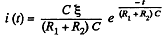
Negative sign is ignored, as we are not interested in the direction of the current.
thus. 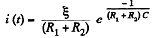 (3)
(3)
When the switch (Sw) is at the position 1, the charge (maximum) accumalated on the capacitor is,
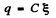
When the Sw is thrown to position 2, the capacitor starts discharging and as a result the electric energy stored in the capacitor totally turns into heat energy tho’ the resistors R1 and R2 (during a very long interval of time). Thus from the energy conservation, the total heat liberated tho the resistors.
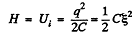
During Hie process of discharging of the capacitor, the current tho’ the resistors and R2 is the same at all the moments of time, thus
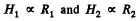
So, 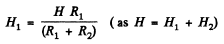
Hence 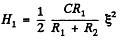
Q. 200. Between the plates of a parallel-plate capacitor there is a metallic plate whose thickness takes η = 0.60 of the capacitor gap. When that plate is absent the capacitor has a capacity C = 20 nF. The capacitor is connected to a de voltage source V = 100 V. The metallic plate is slowly extracted from the gap. Find:
(a) the energy increment of the capacitor;
(b) the mechanical work performed in the process of plate extraction.
Solution. 200. When the plate is absent the capacity of the condenser is
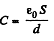
When it is present, the capacity is

(a) The energy increment is clearly.
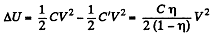
(b) The charge on the plate is
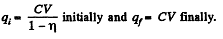
A charge 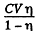 has flown through the battery charging it and withdrawing
has flown through the battery charging it and withdrawing 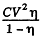 units of energy from the system into the battery. The energy of the capacitor has decreased by just half of this. The remaining half i.e.
units of energy from the system into the battery. The energy of the capacitor has decreased by just half of this. The remaining half i.e. 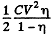 must be the work done by the external agent in withdrawing the plate. This ensures conservation of energy.
must be the work done by the external agent in withdrawing the plate. This ensures conservation of energy.
FAQs on Irodov Solutions: Electric Current - 3 - Airforce X Y / Indian Navy SSR
| 1. What is electric current? |  |
| 2. What factors affect the magnitude of electric current? |  |
| 3. How can electric current be calculated? |  |
| 4. What are the different types of electric current? |  |
| 5. What are some practical applications of electric current? |  |

|
Explore Courses for Airforce X Y / Indian Navy SSR exam
|

|

















