JAMB Mathematics Previous Year Questions: 2020 | Mathematics for JAMB PDF Download
Q1: Evaluate (212)3 - (121)3 + (222)3
(a) (313)3
(b) (1000)3
(c) (1020)3
(d) (1222)3
Ans: (c)
Evaluate (212)3 - (121)3 + (222)3
(212)3 + (222)3 = 12113
→ 12113 - 1213
= 10203
Q2: Factorize (4a + 3)2 - (3a - 2)2
(a) (a + 1)(a + 5)
(b) (a - 5)(7a - 1)
(c) (a + 5)(7a + 1)
(d) a(7a + 1)
Ans: (c)
[(4a + 3)2 - (3a - 2)2 = a2 - b2 = (a + b) (a - b)
= [(4a + 3) + (3a - 2)] [(4a + 3) - (3a - 2)]
= [4a + 3 + 3a - 2] [4a + 3 - 3a + 2]
= (7a + 1)(a + 5)
(a + 5) (7a + 1)
Q3: Find all median of the numbers 89, 141, 130, 161, 120, 131, 131, 100, 108 and 119
(a) 131
(b) 125
(c) 123
(d) 120
Ans: (b)
To find the median, we first arrange in ascending order:
89, 100, 108, 119, 120,130, 131, 131, 141, 161
Since there are even number of items, we take the avarage of the two middle items:
Median = 120 + 130 / 2
= 125
Q4: Find all real number x which satisfy the inequality 1/3 (x + 1) - 1 > 1/5 (x + 4)
(a) x < 11
(b) x < -1
(c) x > 6
(d) x > 11
Ans: (d)
What we need is a solution set that satisfies the given inequality. Each value in the solution set will satisfy the inequality and no other value will satisfy the inequality.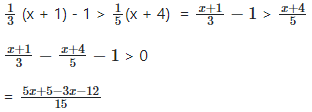
2x - 7 > 15
2x > 22
Divide through by 2:
x > 11
Q5: Express each number in 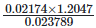 to two significant figures and then evaluate
to two significant figures and then evaluate
(a) 0
(b) 0.9
(c) 1.1
(d) 1.2
Ans: (c)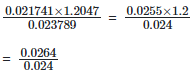
= 1.1
Q6: Four boys and ten girls can cut a field first in 5 hours. If the boys work at 5/4 the rate at which the girls work, how many boys will be needed to cut the field in 3 hours?
(a) 180
(b) 60
(c) 25
(d) 20
Ans: (d)
Let x = numbers of boys that can work at 5/4 the rate as 10 girls
Then,
1 hrs, x boys will work for 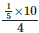
x = 5/4 x 10
= 8 Boys
This means that 8 boys will do the work of ten girls at the same rate
4 + 8 = 12 boys cut the field in 5 hrs for 3 hrs,
12 x 5 / 3 boys will be needed
boys will be needed
Q7: What is the circumference of latitude 0oS if R is the radius of the earth?
(a) cos θ
(b) 2πR cos θ
(c) R sin θ
(d) 2 π r sin θ
Ans: (b)
Circumstances of latitude 0os where R is the radius of the earth 2πr cos θ
Q8: A room is 12m long, 9m wide and 8m high. Find the cosine of the angle which a diagonal of the room makes with the floor of the room
(a) 15/17
(b) 8/17
(c) 8/15
(d) 12/17
Ans: (a)
ABCD is the floor. By pathagoras
AC2 = 144 + 81 = √225
AC = 15cm
Height of room 8m, diagonal of floor is 15m
Therefore, the cosine of the angle which a diagonal of the room makes with the floor is
EC2 = 152 + 82 cosine
= 17
Q9: The goals scored by 40 football teams from three league divisions are recorded below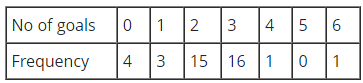 What is the total number of goals scored by all the teams?
What is the total number of goals scored by all the teams?
(a) 21
(b) 40
(c) 91
(d) 96
Ans: (c)
Let x represent number of goals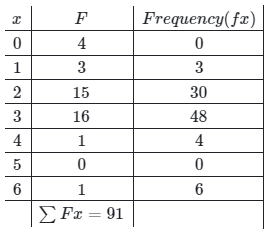 ∑fx = 91
∑fx = 91
Q10: In a class of 150 students, the sector in a pie chart representing the students offering physics has angle 12o. How many students are offering physics?
(a) 18
(b) 15
(c) 10
(d) 5
Ans: (d)
No of students offering physics are
12/360 x 150
= 5
Q11: If log102 = 0.3010 and log103 = 0.4771, eventually without using the logarithm tables, log104.5
(a) 0.3010
(b) 0.4771
(c) 0.6532
(d) 0.9542
Ans: (c)
log102 = 0.3010 and log103 = 04771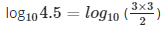
log103 + log103 - log102 = 0.4471 + 0.771 - 0.3010
= 0.6532
Q12: Simplify 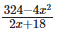
(a) 2(x - 9)
(b) 2(9 + x)
(c) 81 - x2
(d) -2(x - 9)
Ans: (d)
234 - 4x2 = 182 - (2x)2 = (18 - 2x)(18 + 2x)
2x + 18 = 2x + 18 = (2x + 18)
18 - 2x = 2(a - x) or -2(x - a)
Q13: In preparing rice cutlets, a cook used 75g of rice, 40g of margarine, 105g of meat and 20g of bread crumbs. Find the angle of the sector which represent meat in a pie chart?
(a) 30o
(b) 60o
(c) 112.5o
(d) 157.5o
Ans: (d)
Rice = 75g, Margarine = 40g, Meat = 105g
Bread = 20g
Total = 240
Angle of sector represented by meat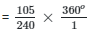
= 157.5
Q14: The angle of a sector of a circle radius 10.5 cm is 48o. Calculate the perimeter of the sector.
(a) 25.4cm
(b) 25.4cm
(c) 25.6cm
(d) 29.8cm
Ans: (d)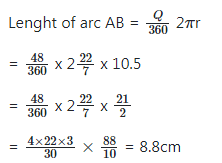
The perimeter = 8.8 + 2r = 8.8 + 2r
= 8.8 + 2(10.5)
= 8.8 + 21
= 29.8cm
Q15: What is the product of 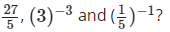
(a) 5
(b) 3
(c) 1
(d) 1/25
Ans: (c)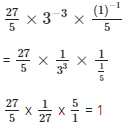
Q16: A crate of soft drinks contains 10 bottle of Coca-Cola 8 of Fanta and 6 of Sprite. If one bottle is selected at random, what is the probability that it is Not a Coca-Cola bottle?
(a) 5/12
(b) 1/3
(c) 3/4
(d) 7/12
Ans: (d)
Coca-Cola = 10 bottles, Fanta = 8 bottles, Spirite = 6 bottles
Total = 24
P(Coca-Cola) = 10/24 : P(not Coca-Cola)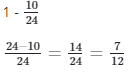
Q17: In this fiqure, PQ = PR = PS and SRT = 68o. Find QPS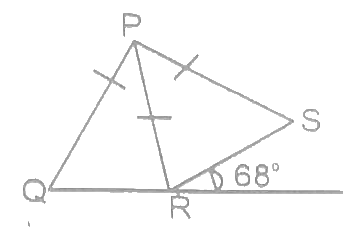 (a) 2
(a) 2
(b) -4
(c) -2
(d) 4
Ans: (c)
Given (-2, 0) ans (0, -4).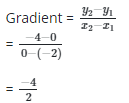
= -2
Q18: Find the equation of the line through the points (5, 7) parallel to the line 7x + 5y = 12.
(a) 5x + 7y = 120
(b) 7x + 5y = 70
(c) x + y = 7
(d) 15x + 17y = 90
Ans: (b)
Equation through (5,7) parallel to the line
7x + 5y = 12
5y = 7x + 12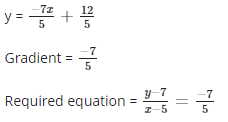
i.e. 5y - 35 = -7x + 35
5y + 7x = 70
Q19: If N225.00 yields N27.00 in x years simple interest at the rate of 4% per annum, find x.
(a) 3
(b) 4
(c) 12
(d) 17
Ans: (a)
Principal = N225.00, interest = N27.00
Year = x, Rate = 4%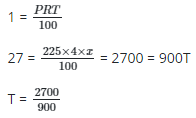
= 3 years
Q20: Calculate the standard deviation of the following data: 7, 8, 9, 10, 11, 12, 13
(a) 2
(b) 4
(c) 12
(d) 17
Ans: (a)
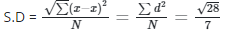
= √4
= 2
Q21: A number is selected at random between 20 and 30, both numbers inclusive. Find the probability that the number is a prime.
(a) 2/11
(b) 5/11
(c) 6/11
(d) 8/11
Ans: (a)
Possible outcomes are 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30. Prime numbers have only two factors, itself and 1. The prime numbers among the group are 23, 29.
The probability of choosing a prime number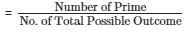
= 2/11
Q22: The equation of the line in the graph is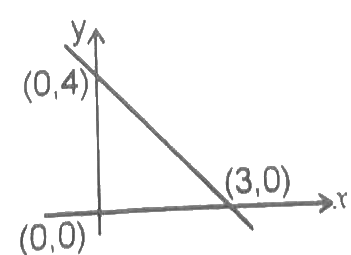 (a) 3y = 3x + 12
(a) 3y = 3x + 12
(b) 3y = 3x + 12
(c) 3y = -4x + 12
(d) 3y = -4x + 9
Ans: (c)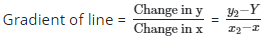
y2 = 01
Y1 = 4
x2 = 3 and x1 = 0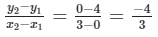
Equation of straight line y = mx + c
Where m = gradient and c = y
intercept = 4
3y = 4x + 23
Q23: Express the product of 0.0014 and 0.011 in standard form
(a) 1.54 x 10−2
(b) 1.54 x 10−3
(c) 1.54 x 10−2
(d) 1.54 x 10−5
Ans: (d)
0.0014 x 0.011 = 0.0000154 = 1.54 x 10-5
Q24: A school boy lying on the ground 30m away from the foot of a water tank towel observes that the angle of elevation of the top of the tank is 60o. Calculate the height of the tank.
(a) 60√3m
(b) 30√3m
(c) 20√3m
(d) 10√3m
Ans: (b)
h = 30 tan 60
= 30√3m
Q25: Find the simple interest rate percent annum at which N1000 accumulates to N1240 in 3 years.
(a) 6%
(b) 8%
(c) 10%
(d) 12%
Ans: (b)
Q26: The pie chart shows the income of a civil servant in month. If his monthly income is N6,000. Find his monthly basic salary. (a) N2,050
(a) N2,050
(b) N2600
(c) N3,100
(d) N3,450
Ans: (a)
360o - (60o + 60o + 67 + 50 = 237o)
360o - 237 = 130o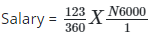
= N2,050
Q27: If x is positive real number, find the range of values for which 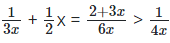
(a) 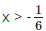
(b) x > 0
(c) 0 < x < 6
(d) 0 < x < 1/6
Ans: (a)
= 4(2 + 3x) > 6x = 12x2 - 2x = 0
= 2x(6x - 1) > 0 = x(6x - 1) > 0
Case 1 (-, -) = x < 0, 6x - 1 > 0
Case 2 (+, +) = x > 0, 6x - 1 > 0 = x > 0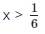
Combining solutions in cases (1) and (2)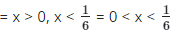
Q28: Find the value of x if 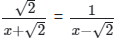
(a) 3√2 + 4
(b) 3√2 - 4
(c) 3 - 2√2
(d) 4 + 2√2
Ans: (a)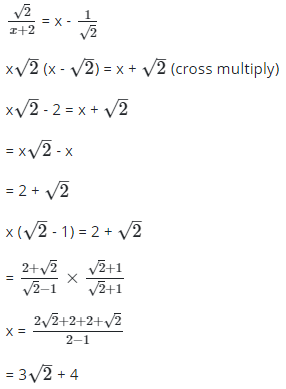
Q29: A binary operation x is defined by a x b = ab. If a x 2 = 2 - a, find the possible values of a?
(a) 1, -2
(b) 2, -1
(c) 2, -2
(d) 1, -1
Ans: (a)
a = b = a2
a + 2 = a2 .....(i)
a + 2 = 2 - a..............(ii)
a2 = 2 - a
a2 + a - 2 = a2 + a - 2 = 0
= (a + 2)(a - 1) = 0
a = 1 or - 2
Q30: The chord ST of a circle is equal to the radius r of the circle. Find the length of arc ST
(a) πr/3
(b) πr/2
(c) πr/12
(d) πr/6
Ans: (a)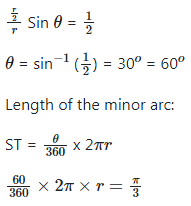
Q31: A sector of circle of radius 7.2cm which substends an angle of 300o at the centre is used to form a cone. What s the radius of the base of the cone?
(a) 8cm
(b) 9cm
(c) 6cm
(d) 7cm
Ans: (a)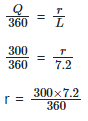
= 8 cm
Q32: A cylindrical tank has a capacity of 3080m3. What is the depth of the tank if the diameter of its base is 14m?
(a) 25m
(b) 23m
(c) 22m
(d) 20m
Ans: (d)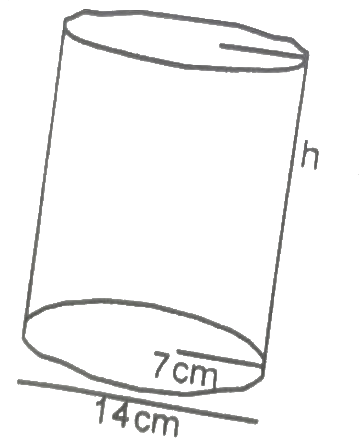 V = 2080cm3, h = ?
V = 2080cm3, h = ?
r = 7cm
Q33: The acres for rice, pineapple, cassava, cocoa and palm oil in a certain district are given respectively as 2, 5, 3, 11 and 9. What is the angle of the sector of cassava in a pie chart?
(a) 180o
(b) 36o
(c) 60o
(d) 108o
Ans: (b)
Total number of acres = 2 + 5 + 3 + 11 + 9 = 30
The angle of acres = 2 + 5 + 3 + 11 + 9 = 30
The angle of the sector for cassava in a pie chart
Q34: Three consecutive terms of a geometric progression are give as n - 2, n and n + 3. Find the common ratio
(a) 3/2
(b) 2/3
(c) 1/2
(d) 1/4
Ans: (a)
n2 = (n + 3) (n - 2)
n2 = n2 + n - 6
n2 + n - 6 - n2 = 0
n - 6 = 0
n = 6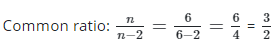
Q35: In a class of 40 students, 32 offer mathematics, 24 offer physics and 4 offer neither mathematics nor physics. How many offer both mathematics and physics?
(a) 4
(b) 8
(c) 16
(d) 20
Ans: (d)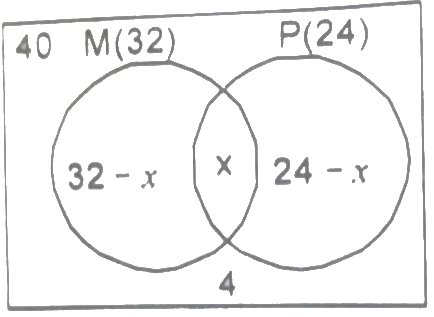 40 = 32 - x + x + 24 + 4
40 = 32 - x + x + 24 + 4
40 = 60 - x
x = 60 - 40
x = 20
Q36: The sum of the interior angle of pentagon is 6x + 6y. Find y in terms of x.
(a) y = 6 - x
(b) y = 90 - x
(c) y = 120 - x
(d) y = 150 - x
Ans: (b)
Sum of interior angles = (2n - 4) 90o
For perntagon, n = 5
Sum of interior angles = 6 x 90o = 540o
6x + 6y = 540o
6(x + y) = 540o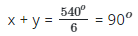
y = 90o
y = 90 - x
Q37: The mean age group of some students is 15years. When the age of a teacher, 45 years old, is added to the ages of the students, the mean of their ages become 18 years. Find the number of students in the group.
(a) 7
(b) 9
(c) 15
(d) 42
Ans: (b)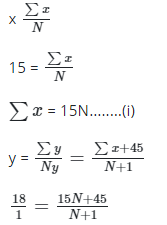
18(N + 1) = 15N + 45
18N + 18 = 15N + 45
18N - 15N = 45 - 18
3N = 27
N = 27/3
= 9
Q38: A surveyor walks 500m up a hill which slopes at an angle of 30o. Calculate the vertical height through which he rises
(a) 252m
(b) 500m
(c) 250m
(d) 255m
Ans: (c) h/500 = sin 30o
h/500 = sin 30o
= 500 sin 30o 
= 250m
Q39: Find the non-zero positive value of x which satisfies the equation
(a) 2
(b) √3
(c) √2
(d) 1
Ans: (c)
The non-zero positive value of x is √2
Q40: Solve the following equation: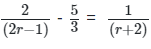
(a) (-1 , 5/2)
(b) (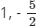 )
)
(c) (5/2 , 1)
(d) (2 , 1)
Ans: (b)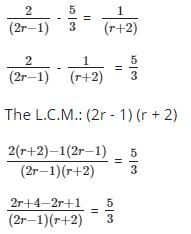
cross multiply the solution
3 * 5 = (2r - 1) (r + 2) * 5
divide both sides 5
3 = 2r2 + 3r - 2 (when expanded)
collect like terms
2r2 + 3r - 2 - 3 = 0
2r2 + 3r - 5 = 0
Factors are -2r and +5r
2r2 -2r + 5r - 5 = 0
[2r2 -2r] [+ 5r - 5] = 0
2r(r-1) + 5(r-1) = 0
(2r+5) (r-1) = 0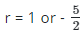
|
139 videos|82 docs|101 tests
|

|
Explore Courses for JAMB exam
|

|

















